Позиционные и непозиционные системы счисления

Система счисления — символический метод записи чисел, представление чисел с помощью письменных знаков.
Система счисления:
· даёт представления множества чисел (целых и/или вещественных);
· даёт каждому числу уникальное представление (или, по крайней мере, стандартное представление);
· отражает алгебраическую и арифметическую структуру чисел.
В непозиционных системах счисления от положения цифры в записи числа не зависит величина, которую она обозначает. Примером непозиционной системы счисления является римская система, в которой в качестве цифр используются латинские буквы.
В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции. Количество используемых цифр называется основанием системы счисления. Место каждой цифры в числе называется позицией. Первая известная нам система, основанная на позиционном принципе – шестидесятeричная вавилонская. Цифры в ней были двух видов, одним из которых обозначались единицы, другим – десятки.
Однако наиболее употребительной оказалась индо-арабская десятичная система. Индийцы первыми использовали ноль для указания позиционной значимости величины в строке цифр. Эта система получила название десятичной, так как в ней десять цифр.
Различие между позиционой и непозиционной систем счисления легче всего понять на примере сравнения двух чисел. В позиционной системе счисления сравнение двух чисел происходит следующим образом: в рассматриваемых числах слева направо сравниваются цифры, стоящие в одинаковых позициях. Бóльшая цифра соответствует бóльшему значению числа. Например, для чисел 123 и 234, 1 меньше 2, поэтому число 234 больше, чем число 123. В непозиционной системе счисления это правило не действует. Примером этого может служить сравнение двух чисел IX и VI. Несмотря на то, что I меньше, чем V, число IX больше, чем число VI.
Позиционные системы счисления
Основание системы счисления, в которой записано число, обычно обозначается нижним индексом. Например, 5557 – число, записанное в семеричной системе счисления. Если число записано в десятичной системе, то основание, как правило, не указывается. Основание системы – это тоже число, и его мы будем указывать в обычной десятичной системе. Вообще, число x может быть представлено в системе с основанием p, как x = an·pn +an – 1·pn–1 + a1·p1 + a0·p0, где an...a0 – цифры в представлении данного числа. Так, например,
103510=1·103 + 0·102 + 3·101 + 5·100;
10102 = 1·23 + 0·22 + 1·21 + 0·20 = 10.
Наибольший интерес при работе на ЭВМ представляют системы счисления с основаниями 2, 8 и 16. Вообще говоря, этих систем счисления обычно хватает для полноценной работы как человека, так и вычислительной машины, однако иногда в силу различных обстоятельств все-таки приходится обращаться к другим системам счисления, например к троичной, семеричной или системе счисления по основанию 32.
Чтобы оперировать с числами, записанными в таких нетрадиционных системах, нужно иметь в виду, что принципиально они ничем не отличаются от привычной десятичной. Сложение, вычитание, умножение в них осуществляется по одной и той же схеме.
Почему же не используются другие системы счисления? В основном, потому, что в повседневной жизни люди привыкли пользоваться десятичной системой счисления, и не требуется никакая другая. В вычислительных же машинах используется двоичная система счисления, так как оперировать числами, записанными в двоичном виде, довольно просто.
Часто в информатике используют шестнадцатеричную систему, так как запись чисел в ней значительно короче записи чисел в двоичной системе. Может возникнуть вопрос: почему бы не использовать для записи очень больших чисел систему счисления, например по основанию 50? Для такой системы счисления необходимы 10 обычных цифр плюс 40 знаков, которые соответствовали бы числам от 10 до 49 и вряд ли кому-нибудь понравится работать с этими сорока знаками. Поэтому в реальной жизни системы счисления по основанию, большему 16, практически не используются.
Непозиционные системы счисления
Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков (бирок): зарубок, черточек, точек.
Позже, для облегчения счета, эти значки стали группировать по три или по пять. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу. Отголоски единичной системы счисления встречаются и сегодня. Так, чтобы узнать, на каком курсе учится курсант военного училища, нужно сосчитать, какое количество полосок нашито на его рукаве. Сами того не осознавая, единичной системой счисления пользуются малыши, показывая на пальцах свой возраст, а счетные палочки используется для обучения учеников 1-го класса счету. Единичная система — не самый удобный способ записи чисел. Записывать таким образом большие количества утомительно, да и сами записи при этом получаются очень длинными. С течением времени возникли иные, более удобные, системы счисления.
Древнеегипетская десятичная непозиционная система счисления. Примерно в третьем тысячелетии до нашей эры древние египтяне придумали свою числовую систему, в которой для обозначения ключевых чисел 1, 10, 100 и т.д. использовались специальные значки — иероглифы.
Все остальные числа составлялись из этих ключевых при помощи операции сложения. Система счисления Древнего Египта является десятичной, но непозиционной.
В непозиционных системах счисления количественный эквивалент каждой цифры не зависит от ее положения (места, позиции) в записи числа.
Например, чтобы изобразить 3252 рисовали три цветка лотоса (три тысячи), два свернутых пальмовых листа (две сотни), пять дуг (пять десятков) и два шеста (две единицы). Величина числа не зависела от того, в каком порядке располагались составляющие его знаки: их можно было записывать сверху вниз, справа налево или вперемежку.
Римская система счисления. Примером непозиционной системы, которая сохранилась до наших дней, может служить система счисления, которая применялась более двух с половиной тысяч лет назад в Древнем Риме. В основе римской системы счисления лежали знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две сложенные ладони) для 10, а для обозначения чисел 100, 500 и 1000 стали применять первые буквы соответствующих латинских слов (Сentum — сто, Demimille — половина тысячи, Мille — тысяча).
Чтобы записать число, римляне разлагали его на сумму тысяч, полутысяч, сотен, полусотен, десятков, пятков, единиц. Например, десятичное число 28 представляется следующим образом:
XXVIII=10+10+5+1+1+1 (три десятка, пяток, три единицы).
Для записи промежуточных чисел римляне использовали не только сложение, но и вычитание. При этом применялось следующее правило: каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него.
Например, IX — обозначает 9, XI — обозначает 11.
Десятичное число 99 имеет следующее представление:
XCIХ = -10+100-1+10.
Римскими цифрами пользовались очень долго. Еще 200 лет назад в деловых бумагах числа должны были обозначаться римскими цифрами (считалось, что обычные арабские цифры легко подделать). Римская система счисления сегодня используется, в основном, для наименования знаменательных дат, томов, разделов и глав в книгах.

8. Перевод чисел из одной системы счисления в другую

В современной вычислительной технике информация чаще всего кодируется с помощью последовательности сигналов всего двух видов: включено или невключено, намагничено или ненамагничено, высокое или низкое напряжение и т.д. Принято обозначать одно состояние цифрой 0, а другое - 1. Такое представление информации в цифровом виде называют двоичным. Набор (последовательность) из нулей и единиц называют двоичным кодом.

Система счисления - совокупность приемов наименования и обозначения чисел. Системы счисления разделяются на две группы: позиционные и непозиционные. Позиционной называется система счисления, в которой значение цифры зависит от ее места (позиции) в ряду цифр, обозначающих число. Системы, не обладающие этим свойством, называются непозиционными (римская система счисления). Основанием позиционной системы счисления называется число цифр, которое используют при записи.

В ЭВМ часто используется восьмеричная и шестнадцатеричная системы счисления. В восьмеричной системе счисления числа записываются с помощью восьми цифр (0 1 2 3 4 5 6 7). Сама восьмерка записывается двумя цифрами: 10. Для записи чисел в шестнадцатеричной системе необходимо уже располагать шестнадцатью различными символами, используемыми как цифры:

10-я: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

16-я: 0 1 2 3 4 5 6 7 8 9 А В С D E F

Пример 1. Переведем десятичное число 45 в двоичную систему счисления.

Правило: Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание и т.д. до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.

46 = 101100₂.

Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.

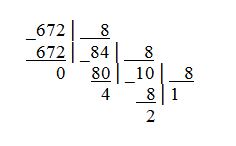
672 = 1240₈.

Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.

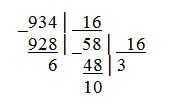
934 = 3А6₁₆.

Пример 4. Переведем в двоичную систему счисления положительную десятичную дробь 0.3.

Правило: Чтобы перевести положительную десятичную дробь в двоичную, нужно дробь умножить на 2. Целую часть произведения взять в качестве первой цифры после запятой в двоичной дроби, а дробную часть вновь умножить на 2. В качестве следующей цифры двоичной дроби взять целую часть этого произведения, а дробную часть произведения снова умножить на 2 и т.д. до получения после запятой заданного количества цифр.

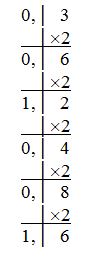
Дробная часть 0,6 уже была на втором шаге вычислений. Поэтому вычисления будут повторяться. Следовательно в двоичной системе счисления число 0,3 представляется периодической дробью:

0,3 = 0,0(1001)₂.

Пример 5. Переведем в двоичную систему счисления положительную десятичную дробь 0,625.

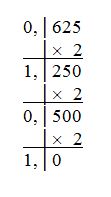
0,625 = 0,101₂.

Замечание: Перевод десятичного числа в двоичную систему счисления проводится отдельно для его целой и дробной части.

Пример 6. Переведем в десятичную систему счисления двоичное число 1011,011.

Правило: Чтобы перевести число из двоичной системы в десятичную систему счисления, нужно двоичное число представить в виде суммы степеней двойки с коэффициентами-цифрами и найти эту сумму.

1011,0112 = 1•2³+0•2²+1•2¹+1•2⁰+0•2^–1+1•2^–2+1•2^–3 =1•8+1•2+1+1•(1/2)2+1•(1/2)3 = 8+2+1+1/4+1/8 = 11,375

1011,011₂ = 11,375₁₀.

Пример 7. Переведем в десятичную систему счисления восьмеричное число 511.

5118 = 5•8²+1•8¹+1•8⁰ =5•64+1•8+1 = 329

511₈ = 329₁₀.

Пример 8. Переведем в десятичную систему счисления шестнадцатеричное число 1151.

1•16³+1•16²+5•16¹+1•16⁰ = 1•4096+1•256+5•16+1 = 4096+256+80+1 = 4433.

1151₁₆ = 4433₁₀.

Пример 9. Переведем двоичное 1100001111010110 число в восьмеричную форму.

Правило: Для преобразования двоичного числа в восьмеричное необходимо двоичную последовательность разбить на группы по три цифры справа налево и каждую группу заменить соответствующей восьмеричной цифрой. Аналогично поступают и при переводе в шестнадцатеричную систему, только двоичную последовательность разбивают не на три, а на четыре цифры.

 

 

Переведем наше число в восьмеричную и шестнадцатеричную системы:

1 100 001 111 010 110 1100 0011 1101 0110

1 4 1 7 2 6 С 3 D 6

Аналогично осуществляется и обратное преобразование: для этого каждую цифру восьмеричного или шестнадцатеричного числа заменяют группой из трех или четырех цифр. Например:

A B 5 1 1 7 7 2 0 4

1010 1011 0101 0001 1 111 111 010 000 100

 

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: