 |
Переходных процессов. Законы коммутации
|
|
|
|
УДК 621.3.011
Г94
Отрецензировано на кафедре «Теоретическая и общая электротехника» Нижегородского государственного технического университета им. Р.Е. Алексеева.
Гуляев, В.В.
Расчет переходных процессов в линейных электрических цепях: метод. пособие для студ. оч. и заоч. обуч. спец-ти 180407 «Эксплуатация судового электрооборудования и средств автоматики» / В.В. Гуляев, А.А. Кралин, А.С. Репин. – Н. Новгород: Изд-во ФГБОУ ВО «ВГУВТ», 2015. – 44 с.
Пособие содержит теоретический материал и примеры решения задач по основным темам раздела «Переходные процессы в линейных электрических цепях» дисциплины «Теоретические основы электротехники». Приведена методика расчета переходных процессов в цепях постоянного и переменного тока классическим и операторным методами. Рассмотрен расчет переходных процессов с использованием интеграла Дюамеля, а также методом переменных состояния. В пособии разобраны многочисленные задачи на все рассмотренные методы расчёта переходных процессов в линейных электрических цепях.
Для студентов очного и заочного обучения.
Работа рекомендована к изданию кафедрой электротехники и электрооборудования объектов водного транспорта (протокол № 11 от 24.05.2012 г.).
© ФГБОУ ВО «ВГУВТ», 2015
Глава 1. Переходные процессы
В линейных электрических цепях
С сосредоточенными параметрами
Рассмотрим определение переходных процессов и методы их анализа. Под переходными процессами понимают процессы перехода от одного установившегося режима электрической цепи к другому установившемуся режиму, отличающемуся структурой цепи или параметрами ее элементов. Наиболее часто переходные процессы вызываются коммутацией, т.е. замыканиями или размыканиями выключателей в цепи. Физически переходные процессы представляют процессы перехода от энергетического состояния цепи в докоммутационном режиме к измененному энергетическому состоянию послекоммутационного режима. Они не могут протекать мгновенно, так как невозможно мгновенное изменение энергии, запасенной в электромагнитном поле цепи.
|
|
|
Переходные процессы обычно являются быстро протекающими и их длительность составляет микро- и миллисекунды, редко достигая длительности секунд. При переходных процессах могут возникать большие перенапряжения, сверхтоки, электромагнитные колебания, которые могут нарушить работу устройства вплоть до аварийного выхода его из строя. С другой стороны, переходные процессы находят широкое практическое применение, например, в различных устройствах силовой электроники, где важно задать закономерности изменения импульсов по амплитуде и частоте при прохождении их через различные функциональные блоки.
Основные методы анализа переходных процессов в линейных цепях:
1. Классический метод, заключающийся в непосредственном интегрировании линейных дифференциальных уравнений, описывающих электромагнитное состояние цепи.
2. Операторный метод, заключающийся в решении системы алгебраических уравнений относительно изображений искомых переменных с последующим переходом от найденных изображений к оригиналам.
3. Метод переменных состояния, представляющий собой упорядоченный способ определения электромагнитного состояния цепи на основе решения системы дифференциальных уравнений первого прядка, записанных в нормальной форме (форме Коши).
4. Метод расчета с помощью интеграла Дюамеля, используемый при сложной форме кривой возмущающего воздействия.
Глава 2. Определение классического метода расчета
|
|
|
переходных процессов. Законы коммутации
Классический метод расчета переходных процессов заключается в непосредственном интегрировании дифференциальных уравнений, описывающих изменения токов и напряжений на участках цепи в переходном процессе. В общем случае при использовании классического метода расчета составляются уравнения электромагнитного состояния цепи по законам Ома и Кирхгофа для мгновенных значений напряжений и токов, связанных между собой на отдельных элементах цепи следующими соотношениями [1]:
– резистор (идеальное активное сопротивление)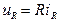 
;
– катушка индуктивности (идеальная индуктивность) 
;
– катушка индуктивности при наличии магнитной связи с катушкой, обтекаемой током 
, 
;
– конденсатор (идеальная емкость) 
, 
.
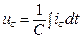Рис. 1
| Рассмотрим электрическую цепь, содержащую последовательно соединенные линейные резистор R, катушку индуктивности L и конденсатор С, при ее подключении к источнику с напряжением u (рис. 1). |
По второму закону Кирхгофа запишем для мгновенных значений уравнение равновесия напряжений:
 .
| (1) |
Подставив в (1) значение тока через конденсатор
получим линейное дифференциальное уравнение второго порядка относительно напряжения на конденсаторе 
:
| (2) |
В общем случае уравнение, описывающее переходный процесс в цепи с n независимыми накопителями энергии, имеет вид:
 ,
| (3) |
где х – искомая функция времени (напряжение, ток, потокосцепление и т.п.); 
– известное возмущающее воздействие (напряжение и (или) ток источника электрической энергии); 
– постоянный коэффициент, определяемый параметрами цепи.
Порядок данного уравнения равен числу независимых накопителей энергии в цепи (катушки индуктивности и конденсаторы в упрощенной схеме, получаемой из исходной путем объединения индуктивностей, соединенных последовательно) и соответственно емкостей, соединения между которыми являются параллельными.
Как известно из математики, общий интеграл линейного дифференциального уравнения (3) представляет собой сумму частного решения исходного неоднородного уравнения и общего решения однородного уравнения, получаемого из исходного путем приравнивания его левой части к нулю. Поскольку с математической стороны не накладывается каких-либо ограничений на выбор частного решения, применительно к электротехнике в качестве последнего удобно принять решение 
, соответствующее искомой переменной х в установившемся послекоммутационном режиме (теоретически для 
).
|
|
|
Частное решение уравнения (3) определяется видом функции 
, стоящей в его правой части, и поэтому называется принужденной составляющей. Для цепей с заданными постоянными или периодическими напряжениями (токами) источников принужденная составляющая определяется путем расчета установившегося режима работы схемы после коммутации любым из рассмотренных в [1] методов расчета линейных электрических цепей.
Вторая составляющая 
общего решения уравнения (3) соответствует режиму, когда внешние (принуждающие) источники энергии на цепь непосредственно не воздействуют. Влияние источников проявляется опосредованно через энергию, запасенную в полях катушек индуктивности и конденсаторов. Данный режим работы схемы называется свободным, а переменная – свободной составляющей.
В соответствии с вышесказанным, общее решение дифференциального уравнения (3) имеет вид
x = + 
| (4) |
Соотношение (4) показывает, что при классическом методе расчета послекоммутационный процесс рассматривается как наложение друг на друга двух режимов – принужденного, наступающего как бы сразу после коммутации, и свободного, имеющего место только в течение переходного процесса. Общее решение (4) дифференциального уравнения (3) определяет значения полного тока или полного напряжения той или иной ветви цепи, которые имеют место в действительности при переходном процессе и могут быть измерены и зафиксированы на осциллограммах.
Необходимо подчеркнуть, что, поскольку принцип наложения справедлив только для линейных систем, классический метод решения, основанный на разложении общего решения (4), справедлив также только для линейных цепей.
В соответствии с определением свободной составляющей в ее математическое выражение входят постоянные интегрирования 
, число которых равно порядку дифференциального уравнения. Постоянные интегрирования находятся из начальных условий, которые принято делить на независимые и зависимые. К независимым начальным условиям относятся потокосцепление (ток) для катушки индуктивности и заряд (напряжение) на конденсаторе в момент времени 
(момент коммутации).
|
|
|
Независимые начальные условия определяются на основании законов (правил) коммутации.
Первый закон (правило) коммутации. Ток через катушку индуктивности L непосредственно до коммутации 
равен току непосредственно после коммутации 
:
 .
| (5) |
Время 
представляет собой время непосредственно до коммутации, 
– после коммутации.
Второй закон (правило) коммутации. Напряжение на конденсаторе непосредственно до коммутации 
равно напряжению непосредственно после коммутации:
 .
| (6) |
Доказать законы коммутации можно от противного: если допустить возможность мгновенного скачка тока индуктивности или напряжения на конденсаторе, то получаются бесконечно большие значения 
и 
, что приводит к нарушению законов Кирхгофа.
Необходимо подчеркнуть, что более общей физической формулировкой законов коммутации является положение о невозможности скачкообразного изменения в момент коммутации для схем с катушкой индуктивности – потокосцеплений, а для схем с конденсаторами – зарядов на них.
Зависимыми начальными условиями называются значения остальных токов и напряжений в схеме (токи через конденсаторы, токи через резисторы, напряжения на индуктивностях, напряжения на резисторах). К ним относят также значения производных от искомой функции, определяемых по независимым начальным условиям при помощи уравнений, составляемых по законам Кирхгофа для момента коммутации . Перечисленные токи, напряжения и их производные могут меняться скачком в момент коммутации, поэтому следует различать докоммутационные (при ) и послекоммутационные (при ) начальные условия.
Необходимое число начальных условий равно числу постоянных интегрирования. Поскольку дифференциальное уравнение вида (3) рационально записывать для переменной, начальное значение которой относится к независимым начальным условиям, задача нахождения начальных условий обычно сводится к нахождению значений этой переменной и ее производных до 
порядка включительно при .
|
|
|
