 |
Глава 3. Алгебраизация системы уравнений
|
|
|
|
Для свободных токов. Характеристическое
Уравнение системы
Свободный ток представляет собой решение однородного дифференциального уравнения, когда внешние (принуждающие) источники энергии на цепь непосредственно не воздействуют. Решение таких уравнений записывают в виде показательных функций 
, и уравнение для каждого свободного тока представляется в виде 
Постоянная интегрирования A для каждого свободного тока определяется отдельно, а показатель затухания p одинаков для всех свободных токов, так как цепь охвачена общим переходным процессом.
Определим производную от свободного тока:
.
Следовательно, производную от свободного тока можно заменить алгебраическим произведением 
и соответственно свободное напряжение на индуктивном элементе 
– на 
.
Определим интеграл от свободного тока и учтем равенство нулю постоянной интегрирования в свободных составляющих тока и напряжения:
.
Следовательно, интеграл от свободного тока можно заменить алгебраическим делением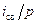 
и соответственно свободное напряжение на конденсаторе 
– на 
.
Алгебраизация исходной системы интегрально-дифференциаль-ных уравнений, составленных для свободных токов электрической цепи на основании законов Кирхгофа или по методу контурных токов, осуществляется заменой символов дифференцирования и интегрирования соответственно умножением и делением на оператор р.
Число полученных алгебраических уравнений равно числу свободных токов электрической цепи, и каждое уравнение имеет нулевую правую часть. В этом случае определитель алгебраизированной системы уравнений свободных токов должен равняться нулю:
 .
| (7) |
Уравнение называют характеристическим уравнением. Единственным неизвестным в нем является показатель затухания p.
|
|
|
Характеристическое уравнение может быть получено следующими способами:
– непосредственно на основе дифференциального уравнения вида (2) путем исключения из системы уравнений, описывающих электромагнитное состояние цепи на основании законов Кирхгофа, всех неизвестных величин, кроме одной, относительно которой и записывается уравнение (2);
– путем использования выражения для входного сопротивления цепи на синусоидальном токе;
– на основе выражения главного определителя алгебраизированной системы уравнений свободных токов.
Согласно первому способу получено дифференциальное уравнение (2) относительно напряжения 
на конденсаторе для последовательного соединения активного сопротивления, индуктивности и конденсатора (см. рис. 1), на основе которого записывается характеристическое уравнение:
 .
| (8) |
Применение второго и третьего способов составления характеристического уравнения рассмотрим на примере цепи рис. 2.
Составление характеристического уравнения по методу входного сопротивления заключается в следующем: записывается входное сопротивление цепи на переменном токе; jω заменяется на оператор р; полученное выражение  приравнивается к нулю.
Уравнение  совпадает с характеристическим. Входное сопротив-
|
Рис. 2
|
ление может быть записано относительно места разрыва любой ветви схемы.
При этом активный двухполюсник заменяется пассивным по аналогии с методом эквивалентного генератора. Данный способ составления характеристического уравнения предполагает отсутствие в схеме магнитосвязанных ветвей; при наличии таковых необходимо осуществить их предварительное развязывание [6].
Для цепи на рис. 2 входное сопротивление относительно зажимов источника составит:
.
Заменив jω на р и приравняв полученное выражение к нулю, запишем:
|
|
|
или
 .
| (9) |
При составлении характеристического уравнения на основе выражения главного определителя алгебраизированной системы уравнений свободных токов следует учесть, что число уравнений равно числу неизвестных свободных составляющих токов. Характеристическое уравнение получается путем приравнивания записанного определителя к нулю. Поскольку выражение для главного определителя не зависит от правых частей системы неоднородных уравнений, его составление можно производить на основе системы уравнений, записанных для полных токов.
Для цепи на рис. 1 алгебраизированная система уравнений на основе метода контурных токов имеет вид:
Отсюда выражение для главного определителя этой системы:
.
Приравняв D к нулю, получим результат, аналогичный (9).
Число корней характеристического уравнения равно степени этого уравнения. Например, если характеристическое уравнение является уравнением первого порядка, то оно имеет один отрицательный действительный корень. Уравнение второй степени, например (8), (9), имеет два корня, которые в зависимости от параметров цепи могут быть следующего типа:
– два действительных неравных отрицательных корня;
– два действительных равных отрицательных корня;
– два комплексно-сопряженных корня с отрицательной действительной частью.
Уравнение третьей степени имеет три корня, которые в зависимости от параметров цепи могут быть следующего типа:
– три действительных неравных отрицательных корня;
– три действительных равных отрицательных корня, из которых два равны друг другу;
– три действительных равных отрицательных корня;
– один действительный отрицательный корень и два комплексно-сопряженных корня с отрицательной действительной частью.
Действительные части корней характеристического уравнения должны быть отрицательными, так как в линейной цепи свободная составляющая тока обязательно затухает во времени ввиду отсутствия в цепи источников ЭДС.
Рассмотрим характер изменения свободных составляющих для переходных процессов в цепях с характеристическим уравнением первой и второй степеней.
Когда характеристическое уравнение является уравнением первого порядка и имеет один отрицательный действительный корень, свободный ток
|
|
|
| (10) |
где 
зависит только от параметров цепи, A – постоянная интегрирования, определяемая начальными условиями.
Свободный ток затухает по экспоненте, и имеет место апериодический переходный процесс. Величину 
называют постоянной времени цепи. Постоянную времени можно интерпретировать как временной интервал, в течение которого свободная составляющая уменьшится в е раз по сравнению с начальным значением. Теоретически переходный процесс длится бесконечно долго. Однако на практике считается, что он заканчивается при 
.
Если характеристическое уравнение второй степени имеет два действительных неравных отрицательных корня (
), то свободный ток складывается из двух экспонент с разными постоянными времени:
| (11) |
Если характеристическое уравнение имеет два действительных равных отрицательных корня (
), то выражение для свободного тока должно быть взято в виде
| (12) |
Если характеристическое уравнение имеет два комплексно-сопряженных корня (
), то свободный ток представляет собой затухающее синусоидальное колебание (колебательный переходный процесс)при угловой частоте 
и начальной фазе 
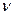. Его выражение записывается в виде
 .
| (13) |
Огибающая колебаний описывается экспонентой 
, где δ – коэффициент затухания.
Поскольку физически колебательный процесс связан с периодическим обменом энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, комплексно-сопряженные корни могут иметь место только для цепей, содержащих емкостной и индуктивный накопители.
В общем случае методика расчета переходных процессов классическим методом включает следующие этапы:
1. Выбор положительных направлений токов в ветвях цепи.
2. Определение токов и напряжений непосредственно до коммутации.
3. Нахождение принужденной составляющей общего решения на основании расчета установившегося режима послекоммутационной цепи.
4. Составление характеристического уравнения и определение его корней. Запись выражения свободной составляющей в форме, определяемой типом найденных корней.
|
|
|
5. Подстановка принужденной и свободной составляющих в соотношение (4) и получение уравнений для полных токов и напряжений.
6. Определение начальных условий и на их основе – постоянных интегрирования.
|
|
|
