 |
Глава 10. Метод переменных состояния
|
|
|
|
Уравнения электромагнитного состояния – это система уравнений, определяющих энергетический режим (состояние) электрической цепи.
Метод переменных состояния основывается на упорядоченном составлении и решении системы дифференциальных уравнений первого порядка, которые разрешены относительно производных, т.е. записаны в виде, наиболее удобном для применения численных методов интегрирования, реализуемых средствами вычислительной техники.
Количество переменных состояния и, следовательно, число уравнений состояния равно числу независимых накопителей энергии. К уравнениям состояния выдвигаются два основных требования:
– независимость уравнений;
– возможность восстановления на основе переменных состояния (переменных, относительно которых записаны уравнения состояния), любых других переменных.
Первое требование удовлетворяется специальной методикой составления уравнений состояния, которая будет рассмотрена далее.
Для выполнения второго требования в качестве переменных состояния следует принять потокосцепления (токи в ветвях с индуктивными элементами) и заряды (напряжения) на конденсаторах. Действительно, зная закон изменения этих переменных во времени, их всегда можно заменить источниками ЭДС и тока с известными параметрами. Остальная цепь оказывается резистивной и, следовательно, всегда рассчитывается при известных параметрах источников. Кроме того, начальные значения этих переменных относятся к независимым, т.е. в общем случае рассчитываются проще других.
При расчете методом переменных состояния, кроме самих уравнений состояния, связывающих первые производные 
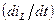и 
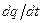
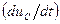с самими переменным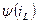и 
и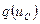 
и источниками внешних воздействий – ЭДС и тока, необходимо составить систему алгебраических уравнений, связывающих искомые величины с переменными состояния и источниками внешних воздействий.
|
|
|
Таким образом, полная система дифференциальных уравнений первого порядка в матричной форме записи имеет вид:
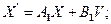
| (30) |
| (31) |
Здесь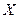 
и 
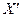– столбцовые матрицы соответственно переменных состояния и их первых производных по времени; 
– столбцовая матрица источников ЭДС и токов, называемая вектором входных величин;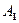 
– квадратная матрица размерностью 
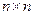(где n – число переменных состояния), определяемая топологией электрической цепи и параметрами ее элементов; 
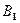– прямоугольная матрица связи между источниками и переменными состояния (количество строк равно n, а столбцов – числу источников m); 
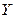– столбцовая матрица выходных (искомых) величин, называемая вектором выходных величин; 
– прямоугольная матрица связи переменных состояния с искомыми величинами (количество строк равно числу искомых величин к, а столбцов – n);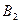 
– прямоугольная размерностью 
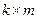матрица связи входных и выходных величин.
Начальные условия для уравнения (30) задаются вектором начальных значений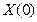 
.
В качестве примера составления уравнений состояния рассмотрим цепь на рис. 20, а, в которой требуется определить токи 
и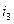 
.
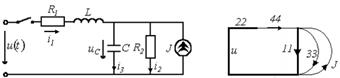
а б
Рис. 20
По законам Кирхгофа для данной цепи запишем уравнения:
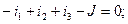
| (32) |
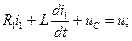
| (33) |
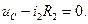
| (34) |
Поскольку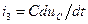 
с учетом соотношения (34) перепишем уравнения (32) и (33) в следующем виде:
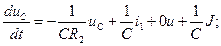
или в матричной форме записи согласно (30):
.
Матричное уравнение вида (31) вытекает из соотношений (32) и (34):
.
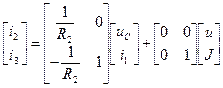Вектор начальных значений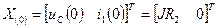 
.
Непосредственное использование законов Кирхгофа при составлении уравнений состояния для сложных цепей может оказаться затруднительным. В этой связи используют специальную методику упорядоченного составления уравнений состояния [Д].
|
|
|
Методика включает в себя следующие основные этапы:
1. Составляется граф схемы (рис. 20, б), к ветвям дерева которого последовательно включаются сначала ветви с источниками ЭДС, затем ветви с конденсаторами. Если дерево не связывает все узлы, то добавляются ветви с резисторами и в последнюю очередь ветви с катушками индуктивности. Дерево, составленное по этим правилам, называют нормальным.
В качестве связей (хорд) сначала выделены источники тока, затем индуктивные элементы, резистивные ветви и в последнюю очередь ветви связи с конденсаторами. Подграф, составленный по этим правилам, называют нормальным подграфом связей (хорд).
2. Осуществляется нумерация ветвей графа (и элементов в схеме), проводимая в следующей последовательности: первыми нумеруются участки графа (схемы) с конденсаторами, затем резисторами, включенными в дерево, следующими нумеруются ветви связи с резисторами и, наконец, ветви с индуктивными элементами (см. рис. 20, б).
3. Составляется таблица, описывающая соединение элементов в цепи. В первой строке таблицы перечисляются емкостные и резистивные элементы дерева, а также источники напряжения (ЭДС). В первом столбце перечисляются резистивные и индуктивные элементы ветвей связи, а также источники тока.
| Процедура заполнения таблицы заключается в поочередном мысленном замыкании ветвей дерева с помощью ветвей связи до получения контура с последующим обходом последнего согласно ориентации соответствующей ветви связи. Со знаком «+» записываются ветви графа, | Таблица 2
|
ориентация которых совпадает с направлением обхода контура, и со знаком «–» ветви, имеющие противоположную ориентацию. Осуществляется расписывание таблицы по столбцам и по строкам. В первом случае получаются уравнения по первому закону Кирхгофа, во втором – по второму. В рассматриваемом случае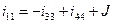 
, откуда в соответствии с нумерацией токов в исходной цепи
.
При расписывании таблицы соединений по строкам напряжения на пассивных элементах необходимо брать со знаками противоположными табличным:
 ;  .
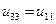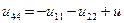| (35) |
Из (35) непосредственно вытекает
.
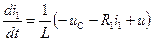Таким образом, формализованным способом получены уравнения, аналогичные составленным выше с использованием законов Кирхгофа.
|
|
|
Вопросы и задачи для самопроверки
1. Как находится общее решение линейного дифференциального уравнения в классическом методе расчета переходных процессов? Объясните понятия принужденной и свободной составляющих общего решения.
2. Сформулируйте законы коммутации с энергетических позиций.
3. В каких электрических цепях и почему возможен колебательный переходный процесс?
4. Определите величину токов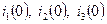 
, напряжений на конденсаторе 
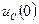и на катушке индуктивности 
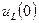в момент коммутации в цепи на рис. 2, если 
Ом; 
Ом, 
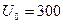В.
5. Сформулируйте понятие характеристического уравнения и получите его в общем виде для схемы на рис. 2.
6. Может ли характеристическое уравнение электрической цепи иметь корни: а) 5–5 j; б) –3 j; в) 5 j, 5 j; г) –8 – 8 j; д) –2 + 3 j, –2 – 3 j; e) –4 + 2 j, 4 + 2 j; ж) –5, 5.
7. Составить характеристическое уравнение для цепи на рис. 2, используя выражение входного сопротивления относительно места разрыва ветви с резистором 
.
8. Почему можно разрывать ветвь с конденсатором и нельзя – ветвь с индуктивным элементом?
9. Для цепи на рис. 21 составить характеристическое уравнение и определить, при каких значениях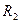 
переходный процесс в ней будет носить апериодический характер, если L = 1 Гн, 
Ом, 
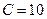мкФ.
10. Определить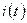 
в цепи на рис. 22, если 
Ом, 
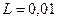Гн,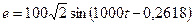 
В, J = 4 А.
Ответ: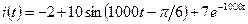 
А.
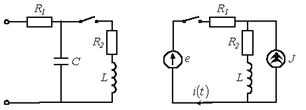
Рис. 21 Рис. 22
11. Определить ток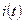 
через катушку индуктивности в цепи на рис. 23, если; 
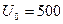В, 
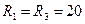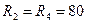Ом;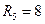 
Ом; 
Ом; 
Гн.
Ответ: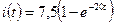 
А.
12. Определить ток 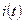в ветви с конденсатором в цепи на рис. 24, если 
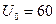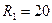Ом; 
Ом;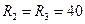 
Ом, L = 0,2 Гн; C = 1 мкФ.
Ответ: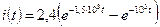 
А.
Рис. 23 Рис. 24
13. Для схемы на рис. 24 изобразите операторную схему замещения и поясните, как в ней учитываются ненулевые независимые начальные условия?
14. Сформулируйте законы Ома и Кирхгофа в операторной форме.
15. Какими способами на практике осуществляется переход от изображения к оригиналу?
16. Какие этапы включает в себя операторный метод расчета переходных процессов?
17. Чему численно соответствуют переходная проводимость и переходная функция по напряжению?
|
|
|
18. Какой принцип лежит в основе метода расчета переходных процессов с использованием интеграла Дюамеля и для каких цепей может быть использован данный метод?
19. Что включает в себя система уравнений при расчете переходного процесса в цепи методом переменных состояния?
20. Перечислите основные этапы методики составления уравнений состояния.
Библиографический список
1. Бессонов, Л.А. Теоретические основы электротехники. Электрические цепи: учебник / Л.А. Бессонов; доп. Мин-вом образов. РФ для студ. вузов электротех. спец. – 11-е изд., испр. и доп. – М.: Гардарики, 2007. – 701 с.
2. Демирчан, К.С. Теоретические основы электротехники. В 3 т. Т. 1: учебник / К.С. Демирчан, Л.Р. Нейман, Н.В. Коровкин; доп. Мин-вом образов. РФ для студ. вузов электротех. спец. – 5-е изд. – СПб.: Питер, 2009. – 512 с.
3. Демирчан, К.С. Теоретические основы электротехники. В 3 т. Т. 2: учебник / К.С. Демирчан, Л.Р. Нейман, Н.В. Коровкин; доп. Мин-вом образов. РФ для студ. вузов электротех. спец. – 5-е изд. – СПб.: Питер, 2009. – 512 с.
4. Шебес, М.Р. Задачник по теории линейных электрических цепей: учеб. пособие для электро- и радиотех. спец. вузов / М.Р. Шебес, М.В. Каблукова – 5-е изд., перераб. и доп. – М.: Высшая школа, 1992. – 544 с.
5. Александров, В.В. Расчет цепей синусоидального тока: учеб. пособие / В.В. Александров, В.В. Гуляев; доп. Мин-вом тр-та РФ для студ. вузов спец. 180404, 180403, 190602. – Н. Новгород: ФГОУ ВПО «ВГАВТ», 2006. – 44 с.
6. Гуляев, В.В. Расчет линейных электрических цепей: учеб. пособие / В.В. Гуляев, А.А. Кралин, А.С. Репин, И.В. Сычушкин. – Н. Новгород: ФГОУ ВПО «ВГАВТ», 2012. – 44 с.
Оглавление
| Глава 1. Переходные процессы в линейных электрических цепях с сосредоточенными параметрами………………... | |
| Глава 2. Определение классического метода расчета переходных процессов. Законы коммутации…………………... | |
| Глава 3. Алгебраизация системы уравнений для свободных токов. Характеристическое уравнение системы………... | |
| Глава 4. Примеры расчета переходных процессов классическим методом…………………………………………... | |
| Глава 5. Операторный метод расчета переходных процессов. Операторное изображение функций, их производных и интегралов……………………………………………. | |
| Глава 6. Законы Ома и Кирхгофа в операторной форме……….. | |
| Глава 7. Переход от изображений к оригиналам. Теорема разложения………………………………………………….. | |
| Глава 8. Последовательность расчета переходных процессов операторным методом. Примеры расчета……………. | |
| Глава 9. Расчет переходных процессов с использованием интеграла Дюамеля……………………………………….. | |
| Глава 10. Метод переменных состояния………………………… | |
| Вопросы и задачи для самопроверки……………………. | |
| Библиографический список ……………………………………….. |
|
|
|
|
|
|
