 |
Глава 4. Примеры расчета переходных процессов
|
|
|
|
Классическим методом
4.1. Переходные процессы в R - L -цепи при подключении её
К источнику постоянного и переменного напряжения
Ток в такой цепи (рис. 3) определяется дифференциальным уравнением

где для источника постоянного напряжения  , для источника переменного напряжения
, для источника переменного напряжения  .
.
Согласно рассмотренной методике для тока можно записать:  . Для постоянного напряжения принужденная составляющая тока . Для постоянного напряжения принужденная составляющая тока  . .
|  Рис. 3
Рис. 3
|
Характеристическое уравнение первого порядка
 ,
,
его единственный корень  и постоянная времени
и постоянная времени  . Таким образом, свободная составляющая тока
. Таким образом, свободная составляющая тока
 .
.
Запишем уравнение полного тока:
 .
.
В соответствии с первым законом коммутации  .
.
По начальным условиям определяем постоянную интегрирования:
 ,
,  .
.
Таким образом, ток в цепи в переходном процессе описывается уравнением
 ,
,
а напряжение на катушке индуктивности – выражением
 .
.
 Рис. 4
Рис. 4
| Качественный вид кривых 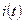 и и  , соответствующих полученным решениям, представлен на рис. 4.
При переменном источнике питания комплексная амплитуда принужденной составляющей рассчитывается с использованием символического метода: , соответствующих полученным решениям, представлен на рис. 4.
При переменном источнике питания комплексная амплитуда принужденной составляющей рассчитывается с использованием символического метода:
|
 ,
,
где амплитудное значение и фаза 
 .
.
Уравнение принужденной составляющей тока:
 .
.
Выражение свободной составляющей не зависит от типа источника напряжения. Следовательно,
 .
.
По начальным условиям определяем постоянную интегрирования:
 .
.
Таким образом, окончательно получаем уравнение полного тока:
 .
.
На рис. 5 приведены графики принужденного, свободного и полного токов.
Выполним анализ полученного выражения полного тока:
1. При начальной фазе напряжения  постоянная интегрирования А = 0. Таким образом, в этом случае ком- постоянная интегрирования А = 0. Таким образом, в этом случае ком-
|
 Рис. 5
Рис. 5
|
мутация не повлечет за собой переходного процесса и в цепи сразу возникнет принужденный установившийся режим.
|
|
|
2. При  свободная составляющая тока максимальна по модулю и ток переходного процесса достигает своей наибольшей величины. Если постоянная времени
свободная составляющая тока максимальна по модулю и ток переходного процесса достигает своей наибольшей величины. Если постоянная времени  значительна по величине, то за полпериода свободная составляющая существенно не уменьшается и максимальная величина тока переходного процесса
значительна по величине, то за полпериода свободная составляющая существенно не уменьшается и максимальная величина тока переходного процесса  может примерно вдвое превышать амплитуду принужденного тока
может примерно вдвое превышать амплитуду принужденного тока  установившегося режима (см. рис. 5). В пределе при
установившегося режима (см. рис. 5). В пределе при  максимальное значение тока переходного режима равно удвоенной амплитуде принужденного тока
максимальное значение тока переходного режима равно удвоенной амплитуде принужденного тока  .
.
Переходные процессы при отключении катушки
Индуктивности от источника питания
| При размыкании ключа (рис. 6) катушка индуктивности отключается от источника и шунтируется разрядным сопротивлением R, соединенным последовательно с обратным диодом. Принужденная составляющая тока через катушку индуктивности равна нулю. Характеристическое уравнение первого порядка |
 Рис. 6
Рис. 6
|
 ,
,
его корень  и постоянная времени
и постоянная времени  .
.
В соответствии с первым законом коммутации
 .
.
Ток через катушку индуктивности и напряжение на ней описываются уравнениями:
 ,
,  .
.
Анализ показывает, что при размыкании цепей, содержащих индуктивные элементы, на них могут возникать большие перенапряжения, которые требуют принятия специальных мер по защите. Действительно, при n = R / Rk >> 1 модуль напряжения на катушке индуктивности в момент коммутации будет превышать напряжение источника:  . При отсутствии разрядного сопротивления указанное напряжение прикладывается к размыкающим контактам, вследствие чего между ними возникает дуга.
. При отсутствии разрядного сопротивления указанное напряжение прикладывается к размыкающим контактам, вследствие чего между ними возникает дуга.
4.3. Переходные процессы в R - С -цепи при ее разряде и заряде
|
|
|


