 |
Анализ и сопоставление экономических и технических параметров продукции производственного назначения в показателе предельной цены
|
|
|
|
На основании проведенного исследования, конкурентоспособность продукции представляет собой оптимальное сочетание цены и качества анализируемого товара. Исходя из этого, при анализе его уровня необходимо исследовать досконально обе ее составляющих, а именно, экономической и технической. Однако, при исследовании экономической составляющей возникают некоторые трудности. Как было указано выше, для осуществления этого процесса необходимо использовать цену потребления, состоящую из двух основных показателей: продажной цены и эксплуатационных расходов. Относительно первой составляющей, в настоящее время ее определяют в большинстве случаев затратным методом, который состоит в суммировании общих издержек и среднего процента прибыли. Однако, данная методика несколько устарела и она не может быть применена для анализа конкурентоспособности, в результате учета в данном экономическом показателе только затрат, необходимых на производство машины, упуская значимость технических и эксплуатационных характеристик. Таким образом, на уровень цены большое влияние оказывает стоимость комплектующих изделий, сырья и материалов.
Как показывает мировая практика, для наиболее точного определения и глубоко анализа потребительной стоимости выпускаемого продукта необходимо использование такого показателя, как предельная цена. В современных условиях под ней понимают уровень цены рассматриваемого оборудования, при назначении которого покупатель, приобретающий исследуемую машину, не получает абсолютно никаких преимуществ по сравнению с приобретением машины-аналога [75]. Под последним понимается тот продукт, производимый конкурирующей фирмой, который должен принципиально точно соответствовать исследуемому оборудованию по своему назначению. Однако, выбранный аналог должен быть не абстрактным продуктом (товаром-идеалом, символизирующим существующую потребность), а машиной, рыночная цена и технические характеристики которой должны быть заведомо известны. Кроме того, несмотря на идентичность назначения, оба рассматриваемых товаров, как машина-аналог, так и анализируемое оборудование, обладают функциональными и классификационными показателями конкретно заданного уровня, которые могут существенно отличаться. Из вышесказанного видно, что при дальнейшем увеличении цены после преодоления уровня предельной исследуемое оборудование становится неконкурентоспособным.
|
|
|
Что касается потребителя, то с его точки зрения процесс ценообразования выглядит несколько иначе, в результате того, что он, приобретая машину, платит не просто за совокупность ресурсов, вложенных в нее производителем, а за те возможности, которые ему эти ресурсы, воплощенные в покупаемое оборудование, предоставляют, то есть, иначе говоря, за выполняемые им функции, совокупность которых характеризуется определенными группами показателей, а именно, классификационными, функциональными и показателями назначения. Таким образом, на данный момент имеем дело с абсолютно разными позициями, даже можно с уверенностью сказать, что эти точки зрения прямо противопоставляются друг другу. Исходя из этого, с целью нахождения общей точки соприкосновения в области ценообразования интересов потребителя и производителя, то есть компромиссного решения создавшейся проблемы, необходимо выведение показателя или группы показателей, которая могла бы отразить позиции обеих сторон. В качестве такого показателя была выбрана масса оборудования [13], в результате того, что она, как и цена машиностроительной продукции имеет функциональную зависимость с показателями назначения.
|
|
|
Вышеизложенное было предложено авторами [13] представить в аналитическом виде:
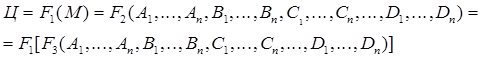 , (2.19)
, (2.19)
где Ц. – предельная цена оборудования;
М – масса машины;
F1 – функция зависимости цены оборудования от его массы;
F2 – функция зависимости цены оборудования от классификационных и функциональных показателей назначения;
F3 – функция зависимости массы оборудования от классификационных и функциональных показателей назначения.
В зависимости от того, для какого вида оборудования проводится анализ, показатели формулы (2.19) принимают соответствующие индексы и тогда формула (2.19) для анализируемого оборудования и машины-аналога принимают следующий вид:
 , (2.20)
, (2.20)
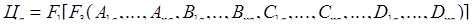 , (2.21)
, (2.21)
где Аi и, Bi и, Ci и, Di и – классификационные и функциональные показатели назначения (линейные, силовые, теоретические, производительные и т.д.) исследуемого оборудования;
Аi а, Bi а, Ci а, Di а – классификационные и функциональные показатели назначения (линейные, силовые, теоретические, производительные и т.д.) машины-аналога.
В случае идеальных экономических отношений, при которых все производители имели бы одинаковые условия производства и вели бы конкурентную борьбу, представляющую собой соперничество за наиболее комфортные, своевременные условия доставки товара потребителю, а, кроме того, направляли бы свою деятельность на конкретную узкую группу потребителей, то есть работало бы в одном сегменте, предлагая им идентичную по своим классификационным и функциональным показателям продукцию, наблюдалась бы ситуация, описываемая следующим равенством:
 . (2.22)
. (2.22)
Однако, в действительности это не достижимо, в результате чего, возникает противоречие между предложением производителя и спросом потребителя, которое состоит в том, что покупатель не занимается сравнением условий производства, а отдает предпочтение тем товарам, потребительская стоимость которых его устраивает. Так как последний показатель у различных производителей обычно не совпадает в результате различных условий производства, неоднородности используемых сырья, материалов и комплектующих изделий, а также под влиянием прочих факторов, то это сказывается как на уровне качества, техническом уровне производимой продукции, так и на потребительской стоимости, что является причиной следующего неравенства:
|
|
|
 . (2.23)
. (2.23)
С целью восстановления равенства между двумя этими показателями необходимо правую часть неравенства (2.23) умножить на поправочный коэффициент, тогда формула (2.23) принимает соответствующий вид:
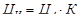 . (2.24)
. (2.24)
Поправочный коэффициент (К), в свою очередь, представляет собой отличие цены исследуемого оборудования (в функциональном представлении) и машины-аналога в относительном выражении:
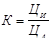 (2.25)
(2.25)
Если учесть существование функциональной зависимости, описанной выражениями (2.20) и (2.21), то уравнение (2.25) будет представлено следующим образом:
 . (2.26)
. (2.26)
Подставив выражение (2.26) в уравнение (2.24), получим функциональную зависимость цены исследуемого оборудования и машины-аналога:
 , (2.27)
, (2.27)
где Ципред. – величина предельной цены исследуемого оборудования.
Как указывают авторы формулы (2.27) [75], недостаточно умножения цены машины аналога на поправочный коэффициент, так как для более точного определения предельной цены исследуемого оборудования, наряду с оговоренными ранее закономерностями необходимо учитывать еще и тот факт, что цена, которую «потребитель готов платить за оборудование производственного назначения при прочих равных условиях прямо пропорциональна отдаче (Qэкс.), которую он (потребитель) от этого оборудования ожидает получить» [75]. Таким образом, для определения изучаемого показателя необходимо учитывать и разницу между техническим уровнем исследуемой машины и аналога. В относительном выражении. эксплуатационная производительность (Qэкс.) определяется с использованием формулы (2.17), то есть на основании основного уравнения функционирования оборудования.
|
|
|
Для корректировки уравнения (2.27) необходимо найти отношение расчетных величин эксплуатационных производительностей (Qэкс.) исследуемого оборудования и машины-аналога. Это действие производится с целью предотвращения двойного учета одних и тех же показателей, в результате того, что все необходимые классификационные и функциональные показатели назначения, которые оказывают влияние на экономическую сторону, уже учтены в выражении (2.27), однако, в нем упускается вышеуказанная прямо пропорциональная зависимость цены от эксплуатационной производительности (Qэкс.). Таким образом, вводимое отношение является еще одним поправочным коэффициентом:
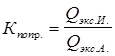 . (2.28)
. (2.28)
где Кпопр. – поправочный коэффициент, учитывающий отличие эксплуатационных производительностей исследуемого оборудования и машины-аналога.
Однако, как замечают авторы [75], для обеспечения достоверности проводимых вычислений необходимо достичь максимального соответствия показателей назначения анализируемого оборудования и машины-аналога. Это действие является обязательным для того, чтобы сформировать единую базу сравнения и выявить экономию или перерасход средств при приобретении того или иного оборудования.
Для достижения вышеописанного эффекта достаточно заменить значения всех классификационных и функциональных показателей назначения аналога, которые учитываются при расчете эксплуатационной производительности машины-аналога (Qэкс.А.) на соответствующие значения присущие исследуемому оборудованию. Таким образом, появляется необходимость определения еще одного показателя, который в дальнейшем будет использоваться как эксплуатационная производительность машины-аналога приведенная к показателям назначения исследуемого оборудования (Qэкс.А..прив.). Исходя из этого, поправочный коэффициент, определяемый по формуле (2.28), примет следующий вид:
 . (2.29)
. (2.29)
Кроме того, по замечаниям тех же авторов, во избежание неточности расчетов требуется проявить аккуратность при определении эксплуатационной производительности обеих видов оборудования, чтобы ни в коем случае не учесть показатели, которые не имеют никакого отношения к характеристикам данного оборудования.
|
|
|
Если учесть все вышеуказанные поправки и подставить формулу (2.29) в уравнение (2.27), то предельная цена исследуемого оборудования теоретически обоснованно может быть определена по формуле (2.30) [75]:
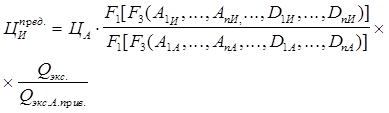 . (2.30)
. (2.30)
Исходя из утверждений существующей методики [75] масса любого оборудования находится в функциональной зависимости от классификационных и функциональных показателей назначения, а именно линейных, силовых, теоретических, производительных и прочих, и выражается функцией F3.
Таким образом, на данном этапе основной задачей является определение и выведение вышеуказанной функции.
Анализ публикаций, направленных на определение массы различных видов оборудования через выведение ее функциональной зависимости от функциональных и классификационных параметров назначения, свидетельствуют о неоспоримом факте, что многим авторам [12; 55] удалось достичь поставленной цели путем построения искомой функции через мультипликативное выражение, которое, кроме теоретической обоснованности, обеспечивает еще и достаточно высокое соответствие расчетных результатов с практическими наблюдениями, что говорит о максимальной пригодности данного метода для использования в реальных производственных условиях.
Опираясь на опыт предыдущих авторов, основная цель дальнейшей работы должна быть направлена на построение в мультипликативной форме эмпирической зависимости. Однако, прежде, чем приступить к этому процессу, необходимо сделать существенное замечание, которое состоит в том, что наиболее весомые показатели назначения, оказывающие существенное влияние на массу оборудования (М), независимо от его класса и вида, могут быть выявлены только на этапе окончательного определения эмпирической формулы, то наиболее компетентные исследователи в данной области научной деятельности советуют проводить анализ этой зависимости первоначально в общем виде, не привязывая его ни к какому-либо конкретному оборудованию. Исходя из этого, вышеуказанная формула в мультипликативной форме имеет следующий вид [92]:
 , (2.31)
, (2.31)
где КМ – коэффициент пропорциональности, определяющий влияние качества исполнения проекта на массу оборудования;
Z1,…, Zn – показатели степени, иначе называемые коэффициентами регрессии, определяющие весомость влияния соответствующих показателей назначения на массу исследуемого вида оборудования.
По свидетельству группы авторов под руководством С.А. Айвозяна, процесс определения эмпирических зависимостей, в том числе и рассматриваемого вида, осуществляется в течение семи, выполняемых в строгой последовательности, этапов [2]. На начальном этапе, прежде всего необходимо определить конечную прикладную цель, для которой и организовано выполнение всех намеченных работ. На момент, когда реализуемые цели поставлены, а исполнителям понятна суть выполняемых задач, есть возможность перехода ко второму этапу, состоящему в сборе статистических данных и информации, необходимых для выполнения поставленных целей и проведения требуемого анализа. Следующим этапом является проведение корреляционного исследования, которое позволяет выявить существование хотя бы какой-то связи, даже незначительно выраженной, между исследуемыми величинами, что сразу же на первоначальной стадии анализа позволит убедиться и определиться, что выполняемые работы имеют теоретическую основу и математический фундамент. Если такая связь найдена, то на четвертом этапе можно переходить к описанию класса функций, в рамках которых будет осуществляться дальнейший поиск и исследование зависимостей. В-пятых, анализируется мультиколлиниарность переменных и производится отбор тех из них, которые являются наиболее информативными. В-шестых, выполняется оценка неизвестных параметров, входящих в исследуемое уравнение статистической связи. И, в результате, при подведении итогов проводимого процесса необходимо проанализировать точность полученного уравнения. В случае недостаточной точности, или несоответствии ее требуемой величине, необходимо пересмотреть весь процесс еще раз с целью выявления ошибок. Однако, если и они не выявлены, то тогда вводится поправочный коэффициент, перекрывающий погрешность расчетов.
Для облегчения весьма трудоемких работ на этапах определения эмпирических зависимостей (кроме первого этапа – постановочного и четвертого этапа, идеи для которого «должны исходить извне статистики» [41]) Л.А. Юрченко разработан соответствующий пакет прикладных программ применительно к персональным ЭВМ «Роботрон 1715» (пакет адаптирован также для ПК типа IBM).
В основу пакета положена универсальная типовая программа управления базами данных «DBASE» [25], возможности которой трансформированы применительно к конкретно решаемой задаче. Для этого сформированы командные файлы, позволяющие реализовать следующие режимные возможности:
а) режим работы с перечнем файлов, позволяющий копировать выбранную базу данных в другой файл, удалить ненужный файл, просматривать списки имен, имеющихся на дискете баз данных и файлов форм печати;
б) режим изменения и просмотра содержимого выбранной базы данных, позволяющий дополнять информацию в конец базы, корректировать и удалять ненужные записи в базе, производить корректировку конкретной строки в базе по ее порядковому номеру;
в) режим выбора информации из заданной базы данных по каким-либо данным;
г) режим печати информации, содержащейся в выбранной базе данных;
д) режим создания и удаления баз данных, позволяющий организовать новую базу данных, изменить структуру любой имеющейся базы, удалить ненужную базу данных;
е) режим связи сформированных баз данных с внешними программами, позволяющий формировать данные для обработки другими программами, необходимыми для определения эмпирических зависимостей, а также пересылать данные из внешних файлов в формируемую базу;
ж) режим сортировки выбранной базы данных по определенному параметру.
Для автоматизации вычислений на последних – шестом и седьмом этапах определения эмпирических зависимостей в пакет включена оригинальная программа установления таких зависимостей методом прямого поиска [104], получившая название «AWTO» (распечатка программы приведена в прил. А).
При написании программы «AWTO» ее создатели использовали следующие основные предпосылки:
1) принята мультипликативная модель построения эмпирических формул; такое решение задачи четвертого этапа процесса определения эмпирических зависимостей вызвано теми обстоятельствами, что, как уже отмечалось ранее, мультипликативная модель наилучшим образом отвечает задачам настоящего исследования, кроме того из теории размерностей [97] известно, что практически любая функция может быть записана как произведение параметров, возведенных в любую степень (т.е. в мультипликативной форме);
2) в качестве критерия точности, т.е. наилучшей сходимости полученного эмпирического уравнения со статистическими данными, использовано условие обеспечения минимального значения коэффициента вариации Квар [97].
Порядок прямого поиска применительно, например, к построению эмпирической формулы определяющей массу грузоподъемных кранов (см. записанное в общем виде выражение) состоит в следующем. Сначала нужно выбрать для каждого из параметров B1, B2,…, Bn начальные предполагаемые значения Z1, Z2,…, Zn вместе с некоторым начальным приращением DZ. Затем по статистическим данным с учетом выбранных значений Z1, Z2,…, Zn по следующей формуле определяются величины Kмi и рассчитывается коэффициент вариации:
 , (2.32)
, (2.32)
где Км – среднее значение Кмi по выборке рассматриваемой базы
данных;
m – количество кранов в выборке.
Следующим шагом является замена какого-либо значения Zi из набора Z1, Z2,…, Zn на величину (Zj + DZ) и, соответственно, определения нового значения Квар. Если значение Квар не уменьшится, испытанию подвергается величина (Zj – DZ). В конечном итоге, по минимуму коэффициента вариации определяется некий локальный оптимум.
Описанный процесс повторяется по определенному алгоритму для каждого из параметров B1, B2,…, Bn в отдельности, а также для сочетания этих параметров, что составляет серию пробных шагов. Новые оценки параметров Z1, Z2,…, Zn образуют некий вектор в пространстве параметров, который задает направление, ведущее к уменьшению Квар. Вдоль этого направления осуществляется ряд рабочих шагов до тех пор, пока при любом изменении значений Z1, Z2,…, Zn уменьшение величины коэффициента вариации окажется невозможным. В области близкой к оптимуму для большей точности величина DZ может быть уменьшена. Невозможность дальнейшего сколько-нибудь существенного снижения значения Квар при малых DZ указывает на то, что достигнут оптимум.
Касательно выбора начального приращения отметим, что Д. Химмельблау [104] считает выбор DZ=0.3 разумным компромиссом между слишком большим начальным размером шага, который придется, возможно, уменьшить прежде, чем начнет уменьшаться величина Квар, и слишком малым размером шага, который может привести к большим затратам времени, так как потребуется сделать очень много малых шагов.
Для исключения возможности нахождения ложных оптимумов можно порекомендовать проводить описанный процесс неоднократно, каждый раз задавая новые, существенно отличные, начальные значения Z1, Z2,…, Zn.
К достоинствам данной методики определения функциональной зависимости можно отнести наиболее высокую точность по сравнению с другими способами, легкость описания, а, в случае, применения программного пакета и быстроту проведения процесса.
Методом, аналогичным определения функциональной зависимости массы оборудования от его показателей назначения, есть возможность выведения уравнения, описывающего зависимость цены оборудования от его массы, то есть функцию F3 формулы (2.19), исходя из этого F3 будет иметь вид:
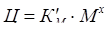 , (2.33)
, (2.33)
где х – показатель степени (коэффициент регрессии), определяющий весомость влияния массы оборудования на его цену.
Кўм – коэффициент пропорциональности, определяющий влияние величины массы на цену оборудования.
Таким образом, подставив формулы (2.31) и (2.33) в уравнение, описывающее определение предельной цены анализируемого оборудования (2.30), получим окончательный вид данного выражения, которое можно использовать для любого класса оборудования [75]:
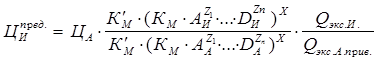 . (2.34)
. (2.34)
Исходя из вышеприведенных доводов, можно сделать вывод о том, что уравнение (2.34) является в настоящее время наиболее удобным для описания экономической стороны исследуемого оборудования, так как оно отражает не только цену машины, но и показывает степень влияния наиболее важных показателей назначения на ее уровень, а также значимость качества и надежности машины при проведения процесса ценообразования. Кроме того, данный показатель позволяет в одном уравнении привести в соответствие и в сравниваемый вид продукцию различных фирм.
|
|
|


