Статистические методы обработки данных

КЛАССИФИКАЦИЯ МАТЕМАТИЧЕСКИХ МЕТОДОВ ОБРАБОТКИ ДАННЫХ

Практическая работа 1

 П ример  

Построение модели зависимости себестоимости книги от ее тиража

 

Данные о себестоимости (у) в у.е. экземпляра книги в зависимости от тиража (х) представлены в таблице.

 

Тираж (х) (тыс. экз.)	1	2	3	4	5
Себестоимость (у) (у. е.)	6	5	4	4	3

 

Предполагается линейная модель зависимости, т.е.

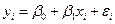, где  .

 

Требуется провести регрессионный анализ зависимости у от х:

1) найти оценки   и  параметров уравнения регрессии ;

2) при   проверить значимость коэффициента регрессии ;

3) при доверительной вероятности 0,95 определить интервальные
оценки для  и условного математического ожидания   в точке х₀=3,
а также интервальную оценку для значения у в точке предсказания х_n+1=6.

Решение

1) Оценки и  параметров линейного уравнения регрессии согласно методу наименьших квадратов найдем по формулам

с учетом, что n=5; , , и  будем иметь:

, ,

тогда оценка уравнения регрессии имеет вид

 .

Для определения несмещенной оценки  остаточной дисперсии  построим вспомогательную таблицу.

 

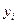
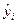
1	6	5,8	0,2
2	5	5,1	-0,1
3	4	4,4	-0,4
4	4	3,7	0,3
5	3	3,0	0,0

 

Тогда несмещенная оценка   равна:

 и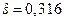

2) проверка значимости коэффициента регрессии , при  сво­дится к проверке нулевой гипотезы H₀: 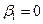 при конкурирующей гипо­тезе H₁: .

Расчетное значение статистики критерия  равно

,

где .

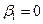Так  , найденного по таблице t-распределения для  и  , то гипотеза H₀:  отвергается с вероятностью ошибки .

Из этого следует, что , т. е. себестоимость книги (у) зависит от тиража;

3) при доверительной вероятности  определим интервальные оценки для , а также для   при .

 Интервальная оценка для коэффициента регрессии имеет вид , где  определяется по таблице t-распределения для  и числа степеней свободы . После подстановки будем иметь   и окончательно .

Таким образом, с вероятностью  можно гарантировать что при увеличении тиража на 1 тыс. экземпляров себестоимость книги умень­шится в лучшем случае на 1,018 у.е., а в худшем на 0,382 у.е.

Согласно

 

интервальная оценка для  в точке х₀ = 4 равнa

, где  определятся по таблице t -распределения при  и  и окончательно .

Таким образом, с вероятностью можно гарантировать, что при тираже 4 тыс. экземпляров себестоимость книги будет находиться в среднем в пределах от 3,15 до 4,25 у.е.

Согласно (2.31) интервальная оценка для значения у в точке х_п+1 = 6 равна:

,

где  определяется по таблице при  и , и окончательно .

Таким образом, с вероятностью  гарантируется, что при тира­же 6 тыс. экземпляров себестоимость книги будет находится в пределах от 0,84 до 3,76 у.е.

Варианты заданий для математической модели балансовых задач

 

Модель межотраслевого баланса, модель Леонтьева

,

                                                 

где X – объем валового выпуска продукции состоит из объёма производственного потребления - AX и объема конечного потребления - Y. Математическая модель позволяет рассчитать объем конечного потребления – Y, если известен объём валового выпуска

.

Рассчитать

1. Значения матрицы А

2.Объем сбалансированного выпуска отраслей X

Варианты исходной информации для заданий

Значение i= N, где N – номер последней цифры в зачетке списку. Значения валового выпуска X определяются исходя из баланса объема валового выпуска и значений конечного потребления и производственного потребления.

 

Номер отрасли	Объём потр. отр. 1	Объём потр. отр. 2	Объём потр. отр. 3	Объём кон. потр. отрасли Y	Объём вал. вып. отрасли X
Отрасль №1	5 + i	35 + i - 1	20 + i	40 + i + 5
Отрасль №2	10 + i	10 + i	20 + i - 3	60 + i + 8
Отрасль №3	20 + i - 2	10 + i + 4	10 + i + 6	10 + i + 7

   

 

Варианты заданий для математической модели задачи линейной торговли

Найти бюджет каждого участника, если задана структурная матрица торговли и общий бюджет:

 

0)

,    у.е.;

1)

,   у.е.;

2)

,   у.е.;

3)

,    у.е.;

 

4)

,     у.е.;

5)

6) ,     у.е.;

,        у.е.;

7)

,       у.е.;

8)

,       у.е.;

9)

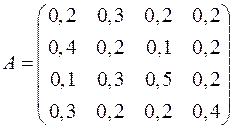,      у.е.

 

Варианты исходной информации для заданий

Значение i= N, где N – номер последней цифры в зачетке списку

 

Варианты заданий для математической модели оптимизационных задач

Математическая модель оптимизационных задач состоит из системы ограничений исследуемого процесса и целевой функции этого процесса, отражающей критерий оптимальности задачи:

 ,                                 (4)

                                                                   (5)

                                                                                     (6)

 Найти оптимальное решение:

1) 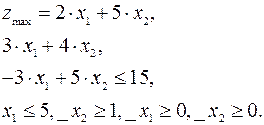 2)

3)                          4)  

  5)               6)         

7)                       8)

Выбор варианта

Номер варианта равен последней цифре в зачетной книжке

Если цифры 9 или 0,то брать задания 1) или 2) 

Варианты заданий для математической модели распределительных  задач

 

Найти оптимальное решение распределительной задачи на минимум затрат Z_min 

 

1)

           

2)   

3)

4)

5)  

    6) 

7)   

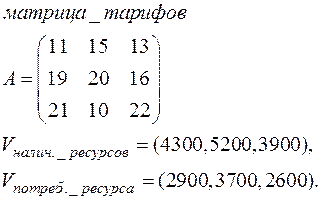
8)   

 

Варианты заданий для математической модели статистических задач

Пусть  в среднем у есть линейная функция от х, т. е. имеет место уравнение регрессии

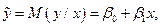
где  — условное математическое ожидание случайной величины у при заданном х. Объясняющая переменная х рассматривается как неслу­чайная величина;

 и — неизвестные параметры генеральной совокупности, которые под­лежат оценке по результатам выборочных наблюдений

Рассчитать оценки  и

№ 1	x	1	2	3	4	5	6	7	8	9	10	11
	Y	13	19	22	14	21	27	16	24	30	19	27

 

№ 2	x	1	2	3	4	5	6	7	8	9	10	11
	Y	8	14	19	11	18	26	16	27	34	20	29

 

№ 3	x	1	2	3	4	5	6	7	8	9	10	11
	Y	10	16	22	14	21	27	20	24	35	25	31

 

№ 4	x	1	2	3	4	5	6	7	8	9	10	11
	Y	11	19	23	15	21	29	19	24	32	23	29

 

№ 5	x	1	2	3	4	5	6	7	8	9	10	11
	Y	14	19	22	17	25	29	19	26	34	22	28

 

№ 6	x	1	2	3	4	5	6	7	8	9	10	11
	Y	15	19	25	18	23	28	20	26	35	23	32

 

№ 7	x	1	2	3	4	5	6	7	8	9	10	11
	Y	6	10	19	10	17	26	16	28	39	21	36

 

№ 8	x	1	2	3	4	5	6	7	8	9	10	11
	Y	7	16	25	12	20	27	18	28	32	20	27

№ 9	x	1	2	3	4	5	6	7	8	9	10	11
	Y	18	26	37	24	29	38	27	38	46	32	41

 

№ 0	x	1	2	3	4	5	6	7	8	9	10	11
	Y	15	19	26	18	24	32	23	30	42	32	41

 

Выбор варианта

Номер варианта равен последней цифре в зачетной книжке

СТАТИСТИЧЕСКИЕ МЕТОДЫ ОБРАБОТКИ ДАННЫХ

12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: