Оценивание коэффициентов многофакторной линейной регрессии

Практическая работа 2

Пример             

Регрессионный анализ фондоотдачи

На основе линейной регрессионной модели исследовать зависимость фондоотдачи в процентах на единицу основных производственных фон­дов (ОПФ) (у) от среднечасовой производительности вращающихся печей (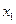) и удельного веса активной части ОПФ ().

В таблице 1  приводятся данные п = 15 цементных заводов страны.

 

Таблица 1

Исходные данные

 

№ п/п	Фондоотдача, y	Среднечасовая производительность печей,	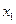Удельный вес активной части ОПФ (%),
1	26	37	39
2	33	33	40
3	24	15	35
4	29	36	48
5	42	26	53
6	24	24	42
7	52	15	54
8	56	33	54
9	26	44	50
10	45	34	53
11	27	63	46
12	54	8	50
13	34	44	43
14	48	43	55
15	45	31	51

Решение

Для определения оценок  согласно

найдем предварительную симметричную матрицу , которая имеет вид

и равна для нашего примера

вектор имеет вид

 

и для нашего примера равен

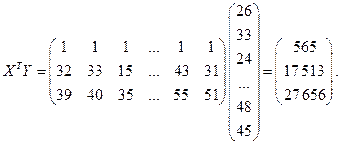
Для получения обратной матрицы  можно воспользоваться методом полного исключения переменных Жордана—Гаусса.

Таким образом, получена обратная матрица:

 

Подставив найденный вектор  и матрицу  в выражение

 

найдем вектор оценок:

Таким образом,

 

И оценка уравнения регрессии имеет вид

.

 

Для проверки значимости уравнения регрессии согласно выражению

 нужно найти  и .

 

Составим вспомогательную таблицу 2

Таблица 2

Вспомогательная таблица

 

1	26	37	39	6,779 073	0,606 954 7
2	33	33	40	29, 532 124	12,026 163
3	24	15	35	27, 615 725	13,073 467
4	29	36	48	40, 643 112	135,562 05
5	42	26	53	51, 290 247	86,308 689
6	24	24	42	35,350 038	128,823 36
7	52	15	54	56,225 982	17,858 923
8	56	33	54	50,613 366	29,015 825
9	26	44	50	41,160 222	229,832 33
10	45	34	53	48,795 751	14,407 725
11	27	63	46	29,212 582	4,895 519 1
12	54	8	50	52,385 454	2,606 758 7
13	34	44	43	30,619 601	11,427 097
14	48	43	55	49,001 049	1,002 099 1
15	45	31	51	49,719 581	2,956 958 8
Итого	565	486	713		690,403 85

Откуда следует, что .

 ;

Проверим на уровне значимости значимость уравнения регрессии.

  H ₀: .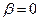

.

По таблице F -распределения для  и чисел степеней свободы  и найдем критическое значение . Так как  гипотеза H ₀:  отвергается, т. е. хотя бы один элемент век­тора  не равен нулю.

Перед проверкой значимости отдельных коэффициентов регрессии найдем оценку ковариационной матрицы  вектора b. Для этого дос­таточно элементы обратной матрицы   умножить на . Тогда будем иметь:

 .

Из статистического смысла ковариационной матрицы следует, что оценки дисперсии коэффициентов уравнения регрессии  соответст­венно равны:

, ,

Проверим значимость коэффициента , т. е. гипотезу H ₀: .

.

По таблице t-распределения для значений  и .

Так как , гипотеза о том, что , не отвергается, т. е.  незначим.

Проверим теперь гипотезу H ₀: .

Так как , гипотеза H ₀: отвергается, т. е. не равен нулю ().

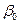Перейдем к алгоритму пошагового регрессионного анализа и исключим из рассмотрения переменную , имеющую незначимый коэффициент , уравнения регрессии. Уравнение регрессии будем искать в виде . Исходные данные для оценки  и , представлены в табл. 3.

 

Таблица 3

Исходные данные

 

1	26	39	25,467 91	0,283 119 7
2	33	40	26,884 0	37,405 456
3	24	35	19,803 55	17,610 192
4	29	48	38,212 72	84,874 209
5	42	53	45,293 17	10,844 968
6	24	42	29,716 18	32,674 713
7	52	54	46,709 26	27,991 929
8	56	54	46,709 26	86.317 849
9	26	50	41,044 9	226,349 01
10	45	53	45,293 17	0,085 948 6
11	27	46	35,380 54	70,233 45
12	54	50	41,044 9	167,834 61
13	34	43	31,132 27	8,223 875 8
14	48	55	43,125 35	0,157 126
15	45	51	42,460 99	6,446 571 7
Итого	565	713		777,191 56

 

Тогда матрица будет 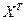иметь вид:

и .

Обратную матрицу вычислим по формуле

,

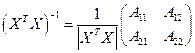где 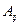 – алгебраическое дополнение к элементу  матрицы .

Найдем определитель матрицы

,

обратную матрицу

 

,

 

и вектор .

Тогда вектор оценок равен:

 

,

а оценка уравнения регрессии имеет вид: .

Из таблицы 3.3 найдем несмещенную оценку остаточной дисперсии:

,

где ,  .

 

Оценка ковариационной матрицы вектора b равна:

.

отсюда .

Для проверки значимости коэффициента β₂, т.е. гипотезы H ₀:  β₂=0, найдем:

.

Определим критическое значение для ;  по табли­це . Так как , нулевая гипотеза отвергается (). Таким образом, окончательно оценка регрессии со значимыми коэффициентами имеет вид

.

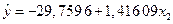Коэффициент регрессии при  показывает, что при росте удельного веса активной части на единицу ОПФ (%) фондоотдача в среднем увели­чивается на 1,416 09 единиц.

Найдем теперь с доверительной вероятностью  интервальную оценку для коэффициента регрессии .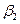

,

где   находим по таблице t-распределения при и . Отсюда

;

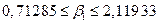
Доверительную границу для условного математического ожидания  у найдем в точке, определяемой вектором начальных условий:  с надежностью .

Предварительно найдем матричное произведение

 

Интервальная оценка для  равна:

.

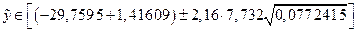Отсюда

и окончательно

.

Таким образом, с доверительной вероятностью мы можем гарантировать, что при значении удельный вес активной части ОПФ завода будет находиться в интервале от 36,403 до 45,686%.

Таблица

Варианты заданий

 

Номер предпри- ятия	Стоимость промышленно- производственных основных фондов, тыс. руб.	Валовая продукция в оптовых ценах предприятия, тыс. руб.	Среднесписочная численность промышленно– производственного персонала, чел.	Среднесписочная численность рабочих, чел.
1	4999	5349	420	331
2	6929	6882	553	486
3	6902	7046	570	498
4	10097	7248	883	789
5	8097	5256	433	359
6	11116	14090	839	724
7	4880	3525	933	821
8	7355	5431	526	428
9	10066	7680	676	607
10	7884	8226	684	619
11	4360	4980	400	318
12	8380	6789	520	419
13	7956	5430	856	327
14	4624	8935	756	624
15	3650	1243	385	129
16	5648	6548	850	758
17	6457	1254	654	546
18	2504	4789	564	410
19	1276	2865	125	108
20	9315	8754	825	564
21	1424	2569	564	420
22	10556	9856	987	876
23	8564	5424	253	213
24	5233	2565	657	540
25	1274	2458	856	756
26	6459	6658	874	712
27	9854	8821	958	814
28	6588	5502	758	615
29	8877	8765	458	314
30	6546	5245	658	512

 

Выбор варианта

 

Студент с последней цифрой i в зачетке выбирает из таблицы 20 строк

 от  i-й до   i+19-й

Если i =0, то от 10-й до 29-й

 

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: