Главная | Обратная связь | Поможем написать вашу работу!

Нахождение maxmin, minmax и седловой точки

⇐ ПредыдущаяСтр 4 из 5Следующая ⇒

Вариант 0

Зная платежную матрицу

определить нижнюю и верхнюю цены игры и найти решение игры.

Вариант 1

Игра задана платежной матрицей. Определить седловую точку.

Вариант 2

Игра задана платежной матрицей. Определить седловую точку.

Вариант 3

Игра задана платежной матрицей. Определить верхнюю цену игры.

Вариант 4

Игра задана платежной матрицей. Определить нижнюю цену игры.

Вариант 5

Игра задана платежной матрицей. Определить нижнюю верхнюю цены игры.

Вариант 6

Игра задана платежной матрицей. Определить седловую точку.

Вариант 7

Игра задана платежной матрицей. Определить седловую точку.

Вариант 8

Игра задана платежной матрицей. Определить седловую точку.

Вариант 9

Игра задана платежной матрицей. Определить седловую точку.

Выбор варианта

Ваш вариант_последняя цифра зачетной книжки

Аналитическое решение игры 2×2 без седловой точки. C оставление сводной таблица основных критериев minmax (Критерий Вальда, Критерий Сэвиджа, Критерий Гурвица, Критерий Лапласа)

Вариант 0

Игра задана платежной матрицей. Определить вероятности P1 и P2 применения стратегий А1 и А2 для оптимальной смешанной стратегии игрока А.

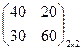
Вариант 1

Вариант 2

Игра задана платежной матрицей. Определить вероятности q1 и q2 применения стратегий В1 и В2 для оптимальной смешанной стратегии игрока В.

Вариант 3

Вариант 4

Игра задана платежной матрицей. Определить цену игры, если вероятности P₁ и P₂ применения стратегий А₁ и А₂ для оптимальной смешанной стратегии игрока A равны 0,6 и 0,4.

Вариант 5

Вариант 6

Вариант 7

Вариант 8

Игра задана платежной матрицей. Определить цену игры, если частоты P1 и P2 применения стратегий А1 и А2 для оптимальной смешанной стратегии игрока A равны соответственно 11/24 и 13/24.

Вариант 9

Выбор варианта

Ваш вариант - последняя цифра зачетной книжки

Решение игр

Вариант 0

Игра задана платежной матрицей. Найти общее решение игры.

Вариант 1

Игра задана платежной матрицей. Найти общее решение игры.

Вариант 2

Игра задана платежной матрицей. Найти общее решение игры.

Вариант 3

Игра задана платежной матрицей. Найти общее решение игры.

Вариант 4

Найти графически стратегии игроков А, В и цену игры, заданной матрицей.

Вариант 5

Найти графически стратегии игроков А, В и цену игры, заданной матрицей.

Вариант 6

Найти графически стратегии игроков А, В и цену игры, заданной матрицей.

Вариант 7

Найти графически стратегии игроков А, В и цену игры, заданной матрицей.

Вариант 8

Найти графически стратегии игроков А, В и цену игры, заданной матрицей.

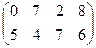
Вариант 9

Игра задана платежной матрицей. Найти общее решение игры.

Выбор варианта

Ваш вариант -предпоследняя цифра зачетной книжки

Практическая работа 5

Применение теории рисков

Расчет чувствительности

Анализ чувствительности основан на последовательно-единичном изменении всех проверяемых на рискованность переменных. На каждом шаге только одна из переменных меняет свое значение на прогнозное число процентов, что приводит к пересчету значения используемого критерия.

В качестве интегральных показателей, характеризующих результаты проекта, обычно рассматривают критерии проектной эффективности (ЧДД – чистый дисконтированный доход; ВНД – внутренняя норма доходности; ИД – индекс доходности./

В ходе классического анализа чувствительности, применяемого к проекту, рассматривается последовательно-единичное влияние на конечный результат проекта (его эффективность) только одного варьируемого параметра (фактора переменной), проверяемого на риск, при сохранении неизменными всех остальных параметров. Обычно при проведении анализа чувствительности выделяют две основные категории факторов по их влиянию:

- на объем поступлений;

- на размеры затрат.

Например, эластичность ЧДД (проекта) по варьируемой переменной определяется как отношение относительного приращения в ЧДД к относительному приращению в варьируемом параметре. Преимуществом показателя эластичности является то, что он – величина безразмерная, т.е. с его помощью удается решить проблему сопоставимости влияния различных (как натуральных, так и стоимостных) варьируемых характеристик проекта:

E= (ЧДД₂ - ЧДД₁ ) / (x ₂ - x ₁), где

x ₁ – базовое значение варьируемой переменной;

x ₂ – измененное значения варьируемой переменной;

ЧДД₁– значение ЧДД для базового варианта расчета;

ЧДД₂ – значение ЧДД для расчета проекта при значении варьируемой переменной, равной x ₂.

По показателям эластичности можно построить «вектор чувствительности», позволяющий выявить наиболее «рискованные» (оказывающие наиболее сильное влияние на ЧДД или другой интегральный показатель эффективности инвестиционного проекта) переменные. Для обеспечения сопоставимости берутся абсолютные значения эластичности, так как знак показывает однонаправленность (если это плюс) или разнонаправленность (если это минус) изменений результирующего и варьируемого параметров. Чем больше эластичность, тем больше внимание должно быть уделено варьируемой переменной, и тем более чувствителен проект к ее изменениям.

Построение рейтинга эластичности (переменные ранжируются по значению показателя эластичности, взятому по модулю) позволяет выявить чувствительные переменные, для которых целесообразно провести дополнительные исследования в рамках количественного анализа рисков.

Экономико-математическая сущность анализа чувствительности состоит в следующем: на основе базового варианта проекта определяют ожидаемое среднее отклонение каждой переменной величины и результаты проекта в случае отклонения одной из переменных величин от базового сценария. Считается, что проект более чувствителен к изменению одного из параметров базового варианта, чем другого, если отклонение первого параметра дает большее отклонение критерия ЧДД – чистого дисконтированного дохода проекта (или другого критерия, выбранного для оценки) по сравнению с базовым критерием.

Проведение анализа чувствительности и выявление наиболее «узких» мест позволяет скорректировать проект и выбрать наиболее безопасную стратегию, то есть такую стратегию его развития и осуществления, которая позволит избежать значительных потерь из-за изменений внешней среды.

Обладая существенными преимуществами, в числе которых объективность, теоретическая прозрачность, простота расчетов, экономико-математическая естественность результатов и наглядность их толкования (именно эти критерии лежат в основе его широкого практического использования), метод анализа чувствительности обладает существенными недостатками, важнейшим из которых является его однофакторность, т.е. ориентированность на изменения только одного фактора проекта, что приводит к недоучету возможной связи между отдельными факторами или недоучету их корреляции. Поэтому при проведении анализа чувствительности проектный аналитик должен выделить переменные, которые будут независимы друг от друга, или, если последнее невозможно, такие переменные, взаимовлияние которых будет минимально. Если же переменные тесно взаимосвязаны, то лучше рассматривать их возможные альтернативные комбинации, что приводит к необходимости анализа сценариев, т.е. к выбору другой техники анализа.

Анализ устойчивости

Метод состоит в разработке сценариев развития проекта в базовом и наиболее опасных вариантах. По каждому сценарию исследуется, как будет действовать в соответствующих организационно-экономических условиях механизм реализации проекта, каковы при этом будут доходы, потери и показатели эффективности у отдельных участников, государства и населения.

Каждому сценарию должны соответствовать:

- набор значений исходных переменных;

- рассчитанные значения результирующих показателей;

- вероятность наступления сценария, определяемая экспертным путем.

Проект считается устойчивым и эффективным, если во всех рассмотренных ситуациях интересы участников соблюдаются, а возможные неблагоприятные последствия устраняются за счет созданных запасов и резервов или возмещаются страховыми выплатами.

Пример 1

Рассмотрим проект строительства многоквартирного дома с последующей продажей квартир на рынке жилья.

С целью упрощения допустим, что в реализации этого проекта задействовано два участника:

1. Компания, имеющая земельный участок и права на его застройку.

2. Строительная фирма "ПодКлюч", рассматривающая возможность заключения контракта с Компанией на строительство. Условия контракта предусматривают, что Компания предоставит земельный участок, всю необходимую проектную документацию, а также понесет все расходы, связанные с оформлением необходимых документов. Кроме того, Компания отвечает за организацию и проведение рекламы. Строительная фирма принимает на себя все расходы, связанные со строительством жилого дома. Доходы от продажи квартир распределены следующим образом:

• 20% квартир безвозмездно передается муниципалитету города,

• по 40% получает каждый участник проекта.

Необходимая информация для расчета устойчивости проекта приведена в табл. 5.

Таблица 5

Показатели	Базовый вариант	Наиболее "опасный" вариант
Общая площадь квартир	1000 кв. м	1000 кв. м
Рыночная стоимость 1 кв.м.	1200 евро	1000 евро _
Оценочная стоимость земельного участка	200,000 евро	200,000 евро
Организационные расходы компании	10,000 евро	15,000 евро _
Реклама	20,000 евро	30,000 евро _
Проектная документация	50,000 евро	70,000 евро
Стоимость строительства 1 кв.м.	300 евро	450 евро

Приведем расчеты, характеризующие устойчивость проекта.

1. По базовому варианту:

ЧДД (Компании) = 0,4 • 1000 кв.м. • 1200 евро - 200,000 евро - 10,000 евро - 20,000 евро - 50,000 евро = 200,000 евро;

ЧДД (Строительной фирмы) = 0,4 • 1000 кв.м • 1200 евро - 300 евро • 1000 кв:м. = 180,000 евро.

2. По наиболее "опасному" варианту:

ЧДД (Компании) = 0,4 • 1000 кв.м. • 1000 евро - 200,000 евро - 15,000 евро - 30,000 евро - 70,000 евро = 85,000 евро;

ЧДД (Строительной фирмы) = 0,4 • 1000 кв.м • 1000 евро - 450 евро • 1000 кв.м. = - 50,000 евро.

Нетрудно увидеть, что проект не является устойчивым. Для того чтобы он был реализован, требуется перераспределить риск увеличения стоимости между участниками проекта.

Пример 2

Расчет рисковых фондов

Одним из подходов планирования резервов является создание так называемого «рискового фонда». По сути, это является самострахованием. Практика самострахования широко распространена в компаниях и на предприятиях. Они формируют страховые фонды: одни в размере 1% от стоимости «активов, другие - 1-5% от объема продаж, третьи - 3-5% от годового фонда выплаты акционерам.

С 1 января 1996г. российским предприятиям разрешено за счет себестоимости создавать страховые фонды в размере не более 1% объема реализованной продукции.

Следует, однако, иметь в виду, что страховой резервный фонд является мертвым капиталом, не приносящим прибыли. Поэтому выбор оптимального размера этого фонда является важной задачей в любой предпринимательской деятельности.

Оптимальный размер такого фонда при управлении проектом - одно из задач управления рисками. Этот размер пропорционален степени риска проекта.

Как отмечалось выше, только на ликвидацию форс-мажорных рисков, как правило, резервируют 7-12% стоимости проекта.

Структура рискового фонда должны быть определена в соответствии со структурой рисков проекта. Для этой цели может быть применена СРР (структура разбиения рисков). При этом необходимо использовать результаты анализа рисков, в результате которого проводится ранжирование рисков по степени их опасности, учитывающей как ущерб от рискового события, так и вероятность его наступления.

Пусть определен рисковый фонд RF в размере k %от бюджета проекта (B).

Этот фонд предназначен для ликвидации последствий n рисков R ₁, R ₂,…, R_n

Эксперты оценили их опасность как О ₁, O ₂,..., О _n,

Тогда доля рискового фонда, предназначенная для ликвидации последствий i -го риска (RF_i), может быть определена как:

Этот же подход, но примененный в обратном порядке, может быть применен для определения общего рискового фонда RF.

Эксперты, определив опасность риска О ₁, O ₂,..., О _n, назначают для каждого из них коэффициент k_i, который будет являться его весом при суммировании и характеризует общепринятый норматив непредвиденных расходов для ликвидации такого риска.

Величина

где p_i — вероятность i -го рискового события,

u_i —ущерб от наступления этого события, характеризует среднюю величину рискового фонда.

Для уточнения величины фонда необходимо учесть вероятностный разброс характеристик u_i.

Окончательно определим RF как

где — коэффициент, отвечающий выбранному уровню надежности, (при уровне опасности 0,95, ).

В проекте выделены 3 особо опасных рисковых события:

1. форс-мажорное (стихийное бедствие)

p₁= 0,01

u₁ = 10 млн. руб.

2. задержка с окончанием работ

p₂ = 0,2

u₂ = 1 млн. руб.

3. перерасход бюджета проекта из-за увеличения процента за кредит

p₃= 0,6

u₃ = 1 млн. руб.

Опасности для этих рисков равны:

O₁ = p₁ u₁ = 100 000

O₂ = p₂ u₂= 200 000

O₃ = p₃ u₃= 600 000

Рассчитаем рисковый фонд по методике, указанной выше. Значения коэффициентов k_i возьмем в соответствии с нормативами, изложенными там же:

k ₁= 10%; k ₂ = 20%; k ₃ = 20%.

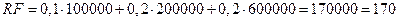тыс.руб.

Так как среднеквадратичное отклонение мало, то поправку к средней величине можно не делать, и взять ее значение тыс. руб. за величину рискового фонда.

⇐ Предыдущая 1 2 345 Следующая ⇒

Воспользуйтесь поиском по сайту: