 |
Реализация метода анализа иерархий для оценки преимуществ расположения жилых фондов в городе Москва
|
|
|
|
Рассмотрим на практике особенности применения метода анализа иерархий. Для этого решим практическую задачу: определим преимущества расположения жилых фондов с учетом многокритериальной оценки размещения жилых зданий в городе Москве. Метод анализа иерархий позволяет разбить сложную проблему на ряд простых подзадач, выявить противоречия. Он не требует упрощения структуры задачи, априорного отбрасывания некоторых признаков. Поэтому он эффективнее других аналитических инструментов позволяет учитывать влияние всевозможных факторов на выбор решения. Метод анализа иерархий проводится по следующей схеме: 1) структурирование проблемы выбора в виде иерархии или; 2) установка приоритетов критериев и оценка каждой из альтернатив по критериям; 3) вычисляются коэффициенты важности для элементов каждого уровня, при этом проверяется согласованность суждений; 4) подсчитывается комбинированный весовой коэффициент и определяется наилучшая альтернатива.
Для проведения анализа были выбраны четыре улицы, расположенные в разных микрорайонах города Москвы: 1-ый Подольский переулок, улица Одинцовская, шоссе Международное, улица Ташкентская. В качестве критериев, по которым будет проводиться оценка жилого фонда, были взяты следующие факторы:
Таблица 1
| Критерии оценки жилых фондов | Название фактора | Желаемое значение |
1. Транспортная доступность в шаговой доступности от метро
2. Свобода парковки наличие парковки рядом с домом, простота подъезда к дому
3. Чистый воздух, экология отсутствие в районе загрязняющих атмосферный воздух и опасных объектов
4. Озелененность территории наличие крупных зеленых массивов (парков) в шаговой доступности от дома
5. Близость от основных объектов в шаговой доступности от школы, инфраструктуры района детского сады, районной поликлиники
|
|
|
Для установления относительной важности элементов иерархии используется шкала отношений. Данная шкала позволяет ЛПР ставить в соответствие степеням предпочтения одного сравниваемого объекта перед другим некоторые числа. Шкала содержит в себе числовые показатели от 1 до 9 и обратные им величины, которые отображают девять степеней превосходства одного критерия над другим. Парные сравнения удобно представлять матрицей. Эта матрица обладает свойством обратной симметричности (aij = 1/aij), где a ij уровень преимущества элемента ui над uj, определяемый по девятибалльной шкале Саати, индексы i и j определяют строку и столбец соответственно. Процесс сравнения важности элементов начинается с левого верхнего элемента матрицы вопросом: насколько первый элемент данного уровня иерархии важнее (относительно элемента верхнего уровня иерархии), чем второй? Далее первый элемент сравнивается с третьим и т.д. Результаты сравнений элементов заносятся в симметричные позиции матрицы. После построения всех матриц парных сравнений на следующем этапе рассчитываются собственные значения векторов и их нормированные оценки.
Для расчетов используются данные 9 экспертов
Й эксперт
| Транспортная доступность | Свобода парковки | Чистый воздух | Озелененность территории | Близость инфраструктуры | |
| Транспортная доступность | 1 | 7 | 3 | 5 | 7 |
| Свобода парковки | 1 | 1 | 1 | 1 | |
| Чистый воздух | 1 | 1 | 1 | ||
| Озелененность территории | 1 | 1 | |||
| Близость инфраструктуры | 1 | ||||
| СУММА |
2-й эксперт
| Транспортная доступность | Свобода парковки | Чистый воздух | Озелененность территории | Близость инфраструктуры | |
| Транспортная доступность | 1 | 1 | 3 | 5 | 9 |
| Свобода парковки | 1 | 1 | 7 | 9 | |
| Чистый воздух | 1 | 3 | 9 | ||
| Озелененность территории | 1 | 3 | |||
| Близость инфраструктуры | 1 | ||||
| СУММА |
|
|
|
3-й эксперт
| Транспортная доступность | Свобода парковки | Чистый воздух | Озелененность территории | Близость инфраструктуры | |
| Транспортная доступность | 1 | 1 | 3 | 5 | 9 |
| Свобода парковки | 1 | 1 | 5 | 9 | |
| Чистый воздух | 1 | 3 | 7 | ||
| Озелененность территории | 1 | 3 | |||
| Близость инфраструктуры | 1 | ||||
| СУММА |
4-й эксперт
| Транспортная доступность | Свобода парковки | Чистый воздух | Озелененность территории | Близость инфраструктуры | |
| Транспортная доступность | 1 | 9 | 7 | 9 | 9 |
| Свобода парковки | 1 | 1 | 3 | 5 | |
| Чистый воздух | 1 | 1 | 3 | ||
| Озелененность территории | 1 | 1 | |||
| Близость инфраструктуры | 1 | ||||
| СУММА |
5-й эксперт
| Транспортная доступность | Свобода парковки | Чистый воздух | Озелененность территории | Близость инфраструктуры | |
| Транспортная доступность | 1 | 3 | 5 | 9 | 9 |
| Свобода парковки | 1 | 1 | 3 | 5 | |
| Чистый воздух | 1 | 1 | 3 | ||
| Озелененность территории | 1 | 1 | |||
| Близость инфраструктуры | 1 | ||||
| СУММА |
6-й эксперт
| Транспортная доступность | Свобода парковки | Чистый воздух | Озелененность территории | Близость инфраструктуры | |
| Транспортная доступность | 1 | 9 | 5 | 9 | 9 |
| Свобода парковки | 1 | 1 | 3 | 1 | |
| Чистый воздух | 1 | 1 | 3 | ||
| Озелененность территории | 1 | 1 | |||
| Близость инфраструктуры | 1 | ||||
| СУММА |
7-й эксперт
| Транспортная доступность | Свобода парковки | Чистый воздух | Озелененность территории | Близость инфраструктуры | |
| Транспортная доступность | 1 | 9 | 7 | 9 | 9 |
| Свобода парковки | 1 | 1 | 5 | 1 | |
| Чистый воздух | 1 | 1 | 1 | ||
| Озелененность территории | 1 | 1 | |||
| Близость инфраструктуры | 1 | ||||
| СУММА |
8-й эксперт
|
|
|
| Транспортная доступность | Свобода парковки | Чистый воздух | Озелененность территории | Близость инфраструктуры | |
| Транспортная доступность | 1 | 9 | 9 | 9 | 7 |
| Свобода парковки | 1 | 1 | 7 | 1 | |
| Чистый воздух | 1 | 1 | 1 | ||
| Озелененность территории | 1 | 1 | |||
| Близость инфраструктуры | 1 | ||||
| СУММА |
9-й эксперт
| Транспортная доступность | Свобода парковки | Чистый воздух | Озелененность территории | Близость инфраструктуры | |
| Транспортная доступность | 1 | 7 | 9 | 9 | 7 |
| Свобода парковки | 1 | 1 | 7 | 1 | |
| Чистый воздух | 1 | 5 | 1 | ||
| Озелененность территории | 1 | 1 | |||
| Близость инфраструктуры | 1 | ||||
| СУММА |
Выбор варианта задания
Если сумма двух последних цифр зачетки студента четная, то меняем местами четные столбцы и строки 2<->4
Если сумма двух последних цифр зачетки студента нечетная, то меняем местами нечетные столбцы и строки 1<->5
Практическая работа 4
Применение теории игр
Задача 1. Найти решение игры, определяемой матрицей
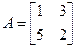
Решение:
Данная игра седловой точки не имеет: α = 2, β = 3. Поэтому ищем решение в смешанных стратегиях:
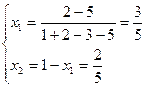
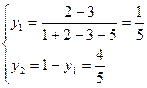
Ответ: Общее решение имеет вид:
; 
; 
.
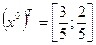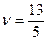Задача 2. Найти решение игры 2x2 с использованием понятия равновесия по Нэшу
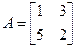
Решение:
Определим по формуле 
математическое ожидание выигрыша игрока А:
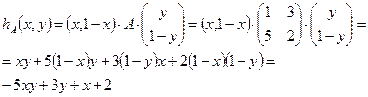
Определим точку Нэша
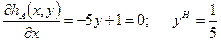
(xH, yH)– координаты точки равновесия по Нэшу.
Таким образом, оптимальные стратегии в данной игре следующие
; 
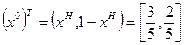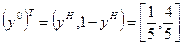
Цена игры в точке Нэша
Ответ: Общее решение имеет вид:
; ; .
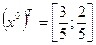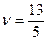Задача 3.
Найти полное решение игры с матрицей
| Bj Ai | B 1 | B 2 |
| A 1 | 2/7 | 3/5 |
| A 2 | 5/8 | 1/3 |
Решение
Решая данную игру в чистых стратегиях
| Bj Ai | B 1 | B 2 | α i |
| A 1 | 2/7 | 3/5 | 3/5 |
| A 2 | 5/8 | 1/3 | 1/3 |
| β j | 5/8 | 3/5 | 1/3 3/5 |
Получаем, что нижняя цена игры α = 1/3, а верхняя цена игры β =3/5. Поскольку α < β, то у матрицы A нет седловых точек. Следовательно, решение игры надо искать в смешанных стратегиях.
|
|
|
По Теорема: Пусть матрица Аразмером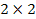 
не имеет седловой точки. Тогда каждый из игроков А и В обладает единственно оптимально смешанной стратегией соответственно 
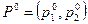и 
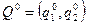, где
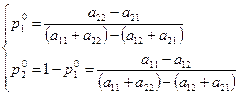
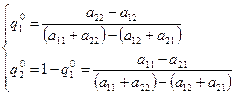
а цена игры (в смешанных стратегиях) V определяется формулой
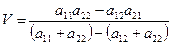
Каждый из игроков A и B обладает единственной оптимальной смешанной стратегией соответственно 
и 
, координаты которых определяются по формулам
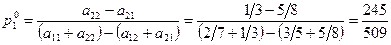
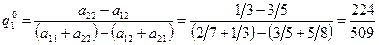
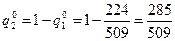
Оптимальной смешанной стратегией игрока A является стратегия P 0 = (245|509, 264|509), а оптимальной смешанной стратегией игрока B является стратегия Q 0 = (224|509, 285|509).
Цена игры будет найдена по формуле
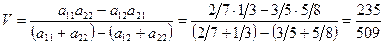
Полное решение игры представляет собой множество { P 0 = (245/509; 264/509); Q 0 = (224/509, 285/509); V = 235/509}.
Задача 4.
Найти с помощью метода Лагранжа решение игры 3x3:
Решение
Определим по формуле v = x 0 T A y 0 математическое ожидание выигрыша игрока А:
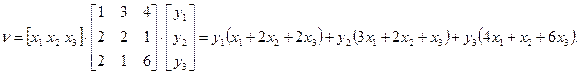
Составим вспомогательные функции ha (х 0, у 0) и hb (х 0, у 0).
ha (х 0, у0) = v + λa (x 1 + x 2 + x 3 - 1);
hb (х 0, у0) = - v + λb (y 1 + y 2 + y 3 - 1).
Запишем системы уравнений для определения точки Нэша:
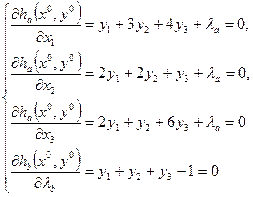
В каждой из систем по 4 уравнения и 4 неизвестных:
y 1 , y 2 , y 3, λ a и x 1 , x 2 , x 3, λ b
Решаем первую систему методом алгебраического сложения. Если вычесть из второго уравнения первое, а затем из второго третье, то получим:
Решаем данную систему и получаем вероятности применения стратегий игрока В:
Аналогично определяется оптимальная стратегия игрока А из второй системы. Если вычесть из первого уравнения второе, а затем из второго третье, то получим:
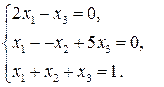
Таким образом, оптимальная стратегия игрока A следующая:
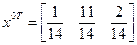
Подставив данные стратегии в выражение для v = x 0 T A y 0, получим значение цены игры
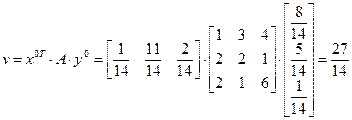
Ответ: 
, 
, 
.
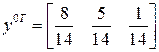Задача 5
Найти решение игры, определяемой матрицей:
| B1 | B2 | B3 | B4 |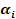 
| |
| A1 | 1 | 3 | 2 | 5 | 1 |
| A2 | 4 | 1 | 2,5 | 0 | 0 |
| 4 | 3 | 2,5 | 5 | 1 2,5 |
Решение:
1. Берем горизонтальный отрезок [0,1].
2. Проводим к нему два перпендикуляра в его концах. На левом перпендикуляре откладываем все элементы первой строки, а на правом перпендикуляре -все элементы второй строки матрицы.
3. Каждую пару точек, изображающих элементы a 1 j и a 2 j j = 1,2,3,4, стоящие в j -м столбце матрицы, соединяем отрезком a 1 j a 2 j. Наивысшая точка нижней огибающей этих отрезков - N. Абсцисса этой точки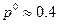 
.
4. Таким образом, единственной оптимальной стратегией игрока А будет смешанная стратегия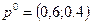 
, придерживаясь которой игрок А случайным образом выбирает свои чистые стратегии А1 и А2 соответственно с вероятностям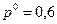и 
и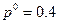 
.
5. Нижней ценой игры в чистых стратегиях является 
.
|
|
|
6. Верхней ценой игры в чистых стратегиях является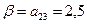 
.
7. Ценой игры является ордината наивысшей точки N нижней огибающей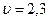 
.
8. Так как нижняя огибающая не имеет наивысших точек, лежащих на перпендикулярах к отрезку [0,1] в его концах, то у данной игры нет седловых точек
. 
9. Через наивысшую точку N нижней огибающей проходят три отрезка - a 12 a 22, a 11 a 21, a 13 a 23.
10. Для определения абсциссы точки N мы можем взять любые два отрезка из указанных трех.
11. Возьмем, например, отрезки a 12 a 22 и a 13 a 23, при j 1 = 2 и j 2 = 3
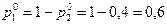
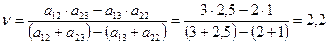
Отметим, что если бы для вычисления значений р 0 и 
мы выбрали другую пару отрезков из указанных трех, то получили бы тот же самый результат.
Ответ: < (0,6 0,4); 2,2 >
Задача 6
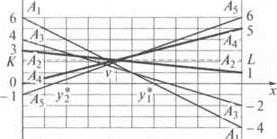
Найти решение следующей игровой задачи графическим способом:
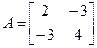
Решение.
Графическая интерпретация данной задачи представлена на рисунке:
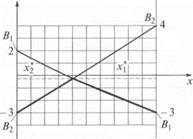
v ≈ - 0.1;
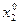≈ 0.42; 
= 1 - 
≈ 0.58;
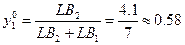
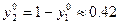
Как видно, полученные результаты практически совпадают с результатами, полученными для той же задачи аналитическим методом и методом, основанным на понятии равновесия по Нэшу.
Ответ: v ≈ - 0.1; S*A = [0.58 0.42]; S*B = [0.58 0.42].
Рассмотрим примеры.
Задача 7.
Определить графическим способом решение игровой задачи 
:
Решение
|
|
Графическая интерпретация данной задачи представлена на рисунке
v = -1.2;
;
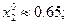
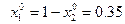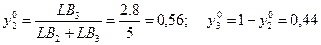
Ответ: v = -1.2;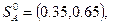 
; 
Задача 8.
Решить графическим способом игровую задачу 
:
Решение.
Графическая интерпретация данной задачи приведена на рисунке
|
|
v = 2.1;
;
; 
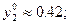
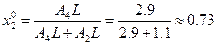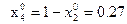
Ответ: v = 2.1;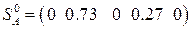 
; 
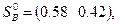
Варианты заданий
|
|
|
