 |
ПР№2. Статистические методы обработки данных
|
|
|
|
Методические рекомендации для компьютерного практикума
ПР№1 Математическая модель расчета строительных конструкций
Задание: решить задачу о изгибе растянуто-изогнутой балки, представленную в теории (задача (1.8.)).
Исходные данные (варианты заданий):
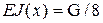 ,
, 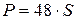 ,
, 
 ,
, 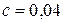
где G - предпоследняя цифра номера зачетной книжки, S- последняя цифра номера зачетной книжки. Представить результаты счета для 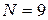 , то есть 8 конечных элементов.
, то есть 8 конечных элементов.
Пример программы на языке Matlab
function Lab
% Задание количества точек разбиения
n=input('Введите n=');
% Задания номера учебной группы (g) и номера студента (s)
g=input('Введите g=');
s=input('Введите s=');
% Задание длины балки
dl=input('Введите dl=');
% Задание жесткости балки
EJ=g/8;
% Задание осевой силы
P=48*s;
% Формирование глобальной матрицы жесткости
% и глобального вектора нагрузок
Kg=zeros(n,n);
Rg=zeros(n,1);
h=dl/(n-1);
Ph=P*h/6;
EJh=EJ/h;
K0=EJh+2*Ph;
K1=Ph-EJh;
Kg(1,1)=1.; Kg(n,n)=1.;
for i=2:n-1
x=(i-1.5)*h;
Rg(i)=(M(x,g,s,dl,EJ,P)+M(x+h,g,s,dl,EJ,P))*h/2;
if(i>2)
Kg(i,i-1)=K1;
end
Kg(i,i)=2*K0;
if(i<n-1)
Kg(i,i+1)=K1;
end
end
% и глобального вектора нагрузок
disp('Глобальная матрица жесткости Kg');
for i=1:n
fprintf('%6.2f',Kg(i,:));
fprintf('\n');
end
disp('Глобальный вектор нагрузок Rg')
fprintf('%12.4f \n',Rg);
% Решение разрешающей системы линейных алгебраических
% уравнений, распечатка результата
y=Kg\Rg;
disp('Вектор-решение y')
fprintf('%12.4f \n',y);
function Res=M(x,g,s,dl,EJ,P)
Res=(g+s)/25.*(2*EJ+P*x*(dl-x));
ПР№2. Статистические методы обработки данных
Однофакторный дисперсионный анализ
Справочная информация по технологии работы с пакетом "Анализ данных" в среде Excel
Режим работы «Однофакторный дисперсионный анализ» служит для выяснения факта влияния контролируемого фактора А на результативный признак Y на основе выборочных данных.
|
|
|
В диалоговом окне данного режима задаются следующие параметры Входной интервал.
1.Группирование.
2. Метки в первой строке/Метки в первом столбце.
4. Альфа — вводится уровень значимости а, равный вероятно-
сти возникновения ошибки первого рода (отвержение нулевой
гипотезы).
5. Выходной интервал/Новый рабочий лист/Новая рабочая книга.
Пример 1. Выборочные данные об объеме работ, выполненных на стройке (за смену) четырьмя бригадами, приведены в табл. 1, сформированной на рабочем листе Microsoft Excel.
Таблица 1
| Объем выполненной работы | ||||
| Номер смены | Бригада 1 | Бригада 2 | Бригада 3 | Бригада 4 |
| 1 | 140 | 150 | 148 | 150 |
| 2 | 144 | 149 | 149 | 155 |
| 3 | 142 | 152 | 146 | 154 |
| 4 | 145 | 150 | 147 | 152 |
При уровне значимости 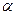 = 0,05 требуется выяснить, зависит ли объем выполненных работ от работающей бригады.
= 0,05 требуется выяснить, зависит ли объем выполненных работ от работающей бригады.
Для решения задачи используем режим работы «Однофакторный дисперсионный анализ».
Но прежде чем проводить анализ данных в сгенерированных таблицах, покажем, как с помощью критерия Бартлетга проверить гипотезу о равенстве генеральных дисперсий Н0:  .
.
Таблица 2
Данные
| B | C | D | E | F | |
| 9 | Бригада 1 | Бригада 2 | Бригада 3 | Бригада 4 | |
| 10 | Число наблюдений | 4 | 4 | 4 | 4 |
| 11 | Оценки 
| 4,92 | 1,58 | 1,67 | 4,92 |
| 12 | Оценки 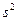
| 3,27 | |||
| 13 | 
| 0,878 | |||
| 14 | 
| 1,540 | |||
| 15 | 
| 7,81 |
Содержимое ячеек в табл. 2:
• в массиве C10:F10 определяются объемы выборок 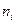 (например, ячейка С10 содержит формулу =СЧЕТ(С5:С8));
(например, ячейка С10 содержит формулу =СЧЕТ(С5:С8));
• в массиве C11:F11 вычисляются несмещенные оценки  групповых дисперсий
групповых дисперсий  (например, ячейка С11 содержит формулу =ДИСП(С5:С8));
(например, ячейка С11 содержит формулу =ДИСП(С5:С8));
• ячейка С12 содержит формулу {=СУММПРОИЗВ(С10:F10-1;C11:F11/CУMM(C10:F10-l)} - рассчитывается объединенная оценка 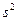 ;
;
• ячейка С13 содержит формулу {=1/(1+1/(3*(4-1))*(СУММ (l/(C10:F10-l))-l/CУMM(C10:F10-l)))} - вычисляется значение коэффициента  ;
;
• ячейка С14 содержит формулу {=С13*СУММПРОИЗВ(С10::F10-1;LN(C12/C11:F11))} - рассчитывается значение критерия Бартлетга wp;
|
|
|
• ячейка С16 содержит формулу =ХИ2ОБР(0,05;3) - определяется значение правосторонней критической точки  .
.
Так как wp = 1,540 не попадает в критическую область (7,81; + 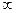 ), то гипотеза Н0:
), то гипотеза Н0: 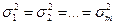 принимается и можно приступить к проверке гипотезы Н0:
принимается и можно приступить к проверке гипотезы Н0: 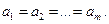 Показатели, рассчитанные в ходе проверки данной гипотезы, представлены в табл. 3 и 4.
Показатели, рассчитанные в ходе проверки данной гипотезы, представлены в табл. 3 и 4.
Таблица 3
| B | C | D | Е | F | ||
| 19 | Однофакторный дисперсионный анализ | |||||
| 20 |
| |||||
| 21 | ИТОГИ | |||||
| 22 | Группы | Счет | Сумма | Среднее | Дисперсия | |
| 23 | Бригада 1 | 4 | 571 | 142,75 | 4,92 | |
| 24 | Бригада 2 | 4 | 601 | 150,25 | 1,58 | |
| 25 | Бригада 3 | 4 | 590 | 147,5 | 1,67 | |
| 26 | Бригада 4 | 4 | 611 | 152,75 | 4,92 | |
Таблица 4
| B | C | D | Е | F | G | H | ||
| 29 | Дисперсионный анализ | |||||||
| 30 | Источник вариации | SS | df | MS | F | P- значение | F критическое | |
| 31 | Между группами | 220,19 | 3 | 73,40 | 22,44 | 3,28Е-0,5 | 3,49 | |
| 32 | Внутри групп | 39,25 | 12 | 3,27 | ||||
| 33 |
| |||||||
| 34 | Итого | 259,44 | 15 | |||||
Табл. 4 называется таблицей однофакторного дисперсионного анализа. Как видим, расчетное значение F -критерия Fp=22,44, а критическая область образуется правосторонним интервалом (3,49; + 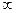 ). Так как Fp попадает в критическую область, то гипотезу H 0 о равенстве групповых математических ожиданий отвергаем, т.е. считаем, что объем ежедневной выборки зависит от работающей бригады.
). Так как Fp попадает в критическую область, то гипотезу H 0 о равенстве групповых математических ожиданий отвергаем, т.е. считаем, что объем ежедневной выборки зависит от работающей бригады.
Выборочный коэффициент детерминации
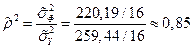
показывает, что 85% общей выборочной вариации ежедневного объема выработки связано с работающей бригадой.
Рассмотрим более подробно механизм расчета основных показателей, представленных в табл. 4.
В ячейке С31 (показатель SS между группами) рассчитывается взвешенная сумма квадратов отклонений групповых средних от общей выборочной средней:
 .
.
В ячейке С32 (показатель SS внутри групп) вычисляется остаточная сумма квадратов отклонений наблюдаемых значений уровня от своей выборочной средней:
 .
.
В ячейке СЗЗ (показатель SS итого) рассчитывается общая сумма квадратов отклонений наблюдаемых значений от общей выборочной средней:
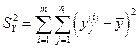 или
или 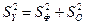 .
.
В ячейках D31.D33 (показатель df) определяются степени свободы:
k ф = m — 1 = 4—1 = 3;
|
|
|
k o =п — т = 16 — 4 = 12;
k Y = (m — 1) + (п — т) = п — 1 = 16 — 1 = 15.
В ячейках Е31:Е32 (показатель MS) вычисляются несмещенные оценки  и
и 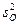 :
:
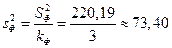 ;
;
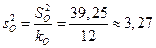 .
.
В ячейке F31 (показатель F)вычисляется расчетное значение критерия Fp:
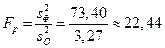 .
.
В ячейке G31 (показатель Р-значение) определяется Р-значение, соответствующее расчетному значение критерия Fp, с помощью формулы
=FPACП(F31;D31;D32).
В ячейке Н31 (показатель F критическое) рассчитывается значение правосторонней критической точки  с помощью формулы
с помощью формулы
=FPACПOБP(0,05;D31;D32)
ПР№2. Многофакторная линейная регрессия
Регрессионный анализ заключается в определении аналитического выражения связи зависимой случайной величины Y (называемой также результативным признаком) с независимыми случайными величинами 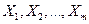 (называемыми также факторами).
(называемыми также факторами).
Форма связи результативного признака Y с факторами 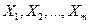 получила название уравнения регрессии. В зависимости от типа выбранного уравнения различают линейную и нелинейную регрессию (в последнем случае возможно дальнейшее уточнение: квадратичная, экспоненциальная, логарифмическая и т. д.).
получила название уравнения регрессии. В зависимости от типа выбранного уравнения различают линейную и нелинейную регрессию (в последнем случае возможно дальнейшее уточнение: квадратичная, экспоненциальная, логарифмическая и т. д.).
В зависимости от числа взаимосвязанных признаков различают парную и множественную регрессию. Если исследуется связь между двумя признаками (результативным и факторным), то регрессия называется парной, если между тремя и более признаками - множественной (многофакторной) регрессией.
При изучении регрессии следует придерживаться определенной последовательности этапов:
1.Задание аналитической формы уравнения регрессии и определение параметров регрессии.
2.Определение в регрессии степени стохастической взаимосвязи результативного признака и факторов, проверка общего качества уравнения регрессии.
3.Проверка статистической значимости каждого коэффициента уравнения регрессии и определение их доверительных интервалов.
Основное содержание выделенных этапов рассмотрим на примере множественной линейной регрессии, реализованной в режиме «Регрессия» надстройки Пакет анализа Microsoft Excel.
Справочная информация по технологии работы
|
|
|
Режим работы «Регрессия» служит для расчета параметров уравнения линейной регрессии и проверки его адекватности исследуемому процессу
В диалоговом окне данного режима задаются следующие параметры:
1.Входной интервал Y — вводится ссылка на ячейки, содержащие данные по результативному признаку. Диапазон должен состоять из одного столбца.
2.Входной интервал X— вводится ссылка на ячейки, содержащие факторные признаки. Максимальное число входных диапазонов (столбцов) равно 16.
3.Метки в первой строке/Метки в первом столбце.
4.Уровень надежности — установите данный флажок в активное состояние, если в поле, расположенное напротив флажка, необходимо ввести уровень надежности, отличный от уровня 95 %, применяемого по умолчанию. Установленный уровень надежности используется для проверки значимости коэффициента детерминации R2 и коэффициентов регрессии аi.
Примечание. При неактивном флажке Уровень надежности в таблице параметров уравнения регрессии генерируются две одинаковые пары столбцов для границ доверительных интервалов.
5.Константа-ноль — установите данный флажок в активное состояние, если требуется, чтобы линия регрессии прошла через начало координат (т. е. а0 = 0).
6.Выходной интервал/Новый рабочий лист/Новая рабочая книга
7.Остатки — установите данный флажок в активное состояние, если требуется включить в выходной диапазон столбец остатков.
8.Стандартизованные остатки — установите данный флажок в активное состояние, если требуется включить в выходной диапазон столбец стандартизованных остатков.
9. График остатков – установите данный флажок в активное состояние, если требуется вывести на рабочий лист точечные грпфики зависимости остатков от факторных признаков 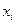 .
.
10. График подбора - установите данный флажок в активное состояние, если требуется вывести на рабочий лист точечные графики зависимости теоретических результативных значений 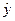 от факторных признаков
от факторных признаков 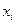 .
.
11. График нормальной вероятности — установите данный флажок в активное состояние, если требуется вывести на рабочий лист точечный график зависимости наблюдаемых значений у от автоматически формируемых интервалов персентилей. График строится на основе генерируемой таблицы «Вывод вероятности»
Пример
Данные о прибыли предприятий Y, величине оборотных средств  и стоимости фондов
и стоимости фондов 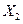 приведены в табл. 1, сформированной на рабочем листе Microsoft Excel.
приведены в табл. 1, сформированной на рабочем листе Microsoft Excel.
Таблица 1
| B | C | D | Е | |
| 2 | Номер предприятия | Прибыль Y, млн руб. | Величина оборотных средств 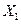 ,
млн руб. ,
млн руб.
| Стоимость основных
фондов 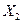 ,
млн руб. ,
млн руб.
|
| 3 | 1 | 188 | 129 | 510 |
| 4 | 2 | 78 | 64 | 190 |
| 5 | 3 | 93 | 69 | 240 |
| 6 | 4 | 152 | 87 | 470 |
| 7 | 5 | 55 | 47 | 110 |
| 8 | 6 | 161 | 102 | 420 |
|
|
|
По представленным данным необходимо определить параметры уравнения линейной регрессии и провести его анализ.
Для решения задачи используем режим работы «Регрессия». Значения параметров, установленных в одноименном диалоговом окне, а рассчитанные в данном режиме показатели - в табл. 2- 6.
Таблица 2
| B | C | |
| 11 | ВЫВОД ИТОГОВ | |
| 12 | ||
| 13 | Регрессионная статистика | |
| 14 | Множественный R | 0,997 |
| 15 | R -квадрат | 0,995 |
| 16 | Нормированный R -квадрат | 0,991 |
| 17 | Стандартная ошибка | 5,050 |
| 18 | Наблюдения | 6 |
В табл. 2 сгенерированы результаты по регрессионной статистике. Эти результаты соответствуют следующим статистическим показателям:
• Множественный R - коэффициенту корреляции R;
• R-квадрат - коэффициенту детерминации R2;
• Стандартная ошибка — остаточному стандартному отклонению
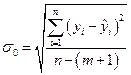 ;
;
• Наблюдения - числу наблюдений п.
В табл. 3 сгенерированы результаты дисперсионного анализа, которые используются для проверки значимости коэффициента детерминации R2.
Таблица 3
| B | C | D | Е | F | G | |
| 20 | Дисперсионный анализ | |||||
| 21 | df | SS | MS | F | Значимость F | |
| 22 | Регрессия | 2 | 13962,33 | 6981,16 | 273,74 | 0,0004 |
| 23 | Остаток | 3 | 76,51 | 25,50 | ||
| 24 | Итого | 5 | 14038,83 | |||
Столбцы табл. имеют следующую интерпретацию:
1. Столбец df - число степеней свободы.
Для строки Регрессия число степеней свободы определяется количеством факторных признаков т в уравнении регрессии 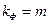 .
.
Для строки Остаток число степеней свободы определяется числом наблюдений п и количеством переменных в уравнении регрессии т + 1: 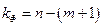 .
.
Для строки Итого число степеней свободы определяется суммой  .
.
2. Столбец SS - сумма квадратов отклонений.
Для строки Регрессия — это сумма квадратов отклонений теоретических данных от среднего:
 .
.
Для строки Остаток - это сумма квадратов отклонений эмпирических данных от теоретических:
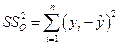 .
.
Для строки Итого - это сумма квадратов отклонений эмпирических данных от среднего:
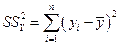 или
или 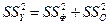 .
.
3. Столбец MS - дисперсии, рассчитываемые по формуле
 .
.
Для строки Регрессия - это факторная дисперсия  .
.
Для строки Остаток - это остаточная дисперсия 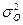 .
.
4.Столбец F - расчетное значение F -критерия Фишера Fp,
вычисляемое по формуле
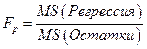 .
.
5. Столбец Значимость F— значение уровня значимости, соответствующее вычисленному значению Fp. Определяется с помощью функции
= FРАСП(Fp; df (pегрессия); df (остаток)).
В табл. 4 сгенерированы значения коэффициентов регрессии ai и их статистические оценки.
Таблица 4
| B | C | D | Е | F | G | H | I | J | |
| 26 | Коэффициенты | Стандартная ошибка | t -статистика | P -значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | |
| 27 | Y- пересечение | -1,94 | 7,63 | -0,25 | 0,82 | -26,21 | 22,32 | -26,21 | 22,32 |
| 28 | Величина оборотных средств 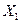 , млн руб. , млн руб.
| 0,69 | 0,20 | 3,53 | 0,04 | 0,07 | 1,32 | 0,07 | 1,32 |
| 29 | Стоимость основных фондов  , млн руб. , млн руб.
| 0,20 | 0,04 | 5,75 | 0,01 | 0,09 | 0,31 | 0,09 | 0,31 |
Столбцы табл. 4 имеют следующую интерпретацию:
1. Коэффициенты - значения коэффициентов ai.
2.Стандартная ошибка - стандартные ошибки коэффициен-
тов аi.
3.t-статистика - расчетные значения t -критерия, вычисляемые по формуле
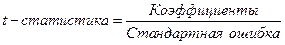 .
.
5. Р-значение - значения уровней значимости, соответствующие
вычисленным значениям t р. Определяются с помощью функции
=СТЬЮДРАСП(t р; п - т - 1).
6. Нижние 95 % и Верхние 95 % — соответственно нижние и
верхние границы доверительных интервалов для коэффициентов
регрессии аi. Для нахождения границ доверительных интервалов с
помощью функции = СТЬДРАСПОБР ( ; п - т - 1) рассчитывается критическое значение t -критерия, а затем по формулам
; п - т - 1) рассчитывается критическое значение t -критерия, а затем по формулам
Нижние 95% = Коэффициент - Стандартная ошибка 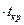 ;
;
Верхние 95% = Коэффициент + Стандартная ошибка 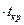 ;
;
вычисляются соответственно нижние и верхние границы доверительных интервалов.
Таблица 5
| B | C | D | Е | |
| 33 | ВЫВОД ОСТАТКА | |||
| 34 | ||||
| 35 | Наблюдение | Предсказанная прибыль Y, млн руб. | Остатки | Стандартные остатки |
| 36 | 1 | 190,91 | -2,91 | -0,74 |
| 37 | 2 | 80,98 | -2,98 | -0,76 |
| 38 | 3 | 94,57 | -1,57 | -0,40 |
| 39 | 4 | 153,62 | -1,62 | -0,42 |
| 40 | 5 | 52,98 | 2,02 | 0,52 |
| 41 | 6 | 153,93 | 7,07 | 1,81 |
В табл. 5 сгенерированы теоретические значения  результативного признака Y и значения остатков. Последние вычисляются как разность между эмпирическими
результативного признака Y и значения остатков. Последние вычисляются как разность между эмпирическими 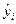 и теоретическими у(значениями результативного признака Y.
и теоретическими у(значениями результативного признака Y.
Таблица 6
| B | C | |
| 33 | ВЫВОД ВЕРОЯТНОСТИ | |
| 34 | ||
| 35 | Персентиль | Прибыль Y, млн руб. |
| 36 | 8,33 | 55 |
| 37 | 25 | 78 |
| 38 | 41,67 | 93 |
| 39 | 58,33 | 152 |
| 40 | 75 | 161 |
| 41 | 91,67 | 188 |
В табл. 6 сгенерированы интервалы персентилей и соответствующие им эмпирические значения у.
Перейдем к анализу сгенерированных таблиц.
Рассчитанные в табл. 4 (ячейки С27 - С29) коэффициенты регрессии ai, позволяют построить уравнение, выражающее зависимость прибыли предприятий Y от величины оборотных средств Х1 и стоимости основных фондов Х2:
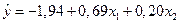 .
.
Значение множественного коэффициента детерминации R2 = 0,995 (ячейка С15 в табл. 2) показывает, что 99,5 % общей вариации результативного признака объясняется вариацией факторных признаков Х1 и Х2. Значит, выбранные факторы существенно влияют на прибыль предприятий, что подтверждает правильность их включения в построенную модель.
Рассчитанный уровень значимости 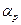 = 0,0004 < 0,05 (показатель Значимость F в табл. 3) подтверждает значимость R2.
= 0,0004 < 0,05 (показатель Значимость F в табл. 3) подтверждает значимость R2.
Другой подход к проверке значимости R2 (как это делалось во всех ранее рассмотренных режимах надстройки «Пакет анализа») основан на проверке попадания Fp (показатель F табл. 3) в критическую область ( ,
, 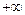 ). Для рассматриваемого примера
). Для рассматриваемого примера 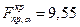 , которое рассчитывается по формуле
, которое рассчитывается по формуле
=FPACПOБP(0,05;C22;C23),
где в ячейке С22 вычисляется число степеней свободы kф = т = 2, а
в ячейке С23 - число степеней свободы k О = n —(m +1)=6—(2 + 1) =3.
Так как Fp = 273,74 попадает в критический интервал (9,55; 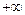 ), то гипотеза Н0: R2 = 0 отвергается, т. е. коэффициент детерминации R2 является значимым.
), то гипотеза Н0: R2 = 0 отвергается, т. е. коэффициент детерминации R2 является значимым.
Показатель средней ошибки аппроксимации 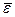 = 2,7 % также подтверждает достаточно высокую адекватность построенного уравнения. Данный показатель может быть рассчитан по формуле
= 2,7 % также подтверждает достаточно высокую адекватность построенного уравнения. Данный показатель может быть рассчитан по формуле
{=CУMM(ABS(D36:D41)/(C3:C8))/CЧET(C3:C8)*100},
где в массиве D36: D41 табл. 5 рассчитаны разности между эмпирическими и теоретическими значениями результативного признака.
Следующим этапом является проверка значимости коэффициентов регрессии: a 0, а1 и а2. Сравнивая попарно элементы массивов С27:С29 и D27:D29 (см. табл. 4), видим, что абсолютное значение свободного члена а0 меньше, чем его стандартная ошибка. Таким образом, свободный член а0 следует исключить из уравнения регрессии.
Стандартные ошибки коэффициентов а1 и а2 меньше своих стандартных ошибок. К тому же эти коэффициенты являются значимыми, о чем можно судить по значениям показателя Р-значение в табл. 4, которые меньше заданного уровня значимости 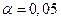 .
.
Другой распространенный способ проверки значимости коэффициентов регрессии основан на проверке попадания tp (показатель t-cmamucmика в табл. 4) в критическую область 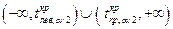 . В генерируемых таблицах режима не приводится значение /™ но его можно легко вычислить с помощью функции СТЬЮДРАСПОБР Для рассматриваемого примера значение
. В генерируемых таблицах режима не приводится значение /™ но его можно легко вычислить с помощью функции СТЬЮДРАСПОБР Для рассматриваемого примера значение 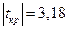 , которое рассчитывается по формуле
, которое рассчитывается по формуле
=СТЬЮДРАСПОБР(0,05;6-2-1),
где 0,05 — заданный уровень значимости;
0 — число наблюдений;
2 — число факторов в уравнении регрессии;
1 — число свободных членов в уравнении регрессии.
Так как 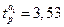 и
и  попадают в критический интервал
попадают в критический интервал 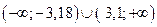 , то коэффициенты регрессии а1 и а2 являются значимыми.
, то коэффициенты регрессии а1 и а2 являются значимыми.
Подводя итог предварительному анализу уравнения регрессии, можно сделать вывод, что его целесообразно пересчитать без свободного члена a 0, который не является статистически значимым.
Для пересчета уравнения регрессии в диалоговом окне Регрессия необходимо задать те же самые параметры, за исключением лишь того, что следует активизировать флажок Константа-ноль. В случае если незначимым является коэффициент при факторном признаке, следует пересмотреть набор признаков в уравнении регрессии.
После пересчета уравнения на рабочем листе генерируются таблицы, аналогичные табл. 2-6. Для сравнения приведем только первые три из них (табл. 7—9).
Таблица 7
| B | C | |
| 11 | ВЫВОД ИТОГОВ | |
| 12 | ||
| 13 | Регрессионная статистика | |
| 14 | Множественный R | 0,997 |
| 15 | R -квадрат | 0,994 |
| 16 | Нормированный R -квадрат | 0,743 |
| 17 | Стандартная ошибка | 4,421 |
| 18 | Наблюдения | 6 |
Таким образом, получаем новое уравнение регрессии:
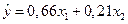 .
.
Проверка значимости коэффициента детерминации R2 и коэффициентов а1 и а2 при факторных признаках подтверждает адекватность полученного уравнения.
Экономическая сущность коэффициентов а1 и а2 в полученном уравнении регрессии состоит в том, что они показывают степень влияния каждого фактора на прибыль предприятий. Так,
Таблица 8
| B | C | D | Е | F | G | |
| 20 | Дисперсионный анализ | |||||
| 21 | df | SS | MS | F | Значимость F | |
| 22 | Регрессия | 2 | 13960,67 | 6980,33 | 357,21 | 0,0003 |
| 23 | Остаток | 4 | 78,16 | 19,54 | ||
| 24 | Итого | 6 | 14038,83 | |||
Таблица 9
| B | C | D | Е | F | G | H | I | J | |
| 26 | Коэффициенты | Стандартная ошибка | t -статистика | P -значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | |
| 27 | Y- пересечение | 0 | # Н/Д | # Н/Д | # Н/Д | # Н/Д | # Н/Д | - # Н/Д | # Н/Д |
| 28 | Величина оборотных средств  , млн руб. , млн руб.
| 0,66 | 0,11 | 5,95 | 0,004 | 0,35 | 0,96 | 0,35 | 0,96 |
| 29 | Стоимость основных фондов  , млн руб. , млн руб.
| 0,21 | 0,03 | 7,65 | 0,002 | 0,13 | 0,28 | 0,13 | 0,28 |
увеличение оборотных средств на 1 млн руб. ведет к росту прибыли на 0,66 млн руб., а увеличение основных фондов на 1 млн руб. ведет к росту прибыли на 0,21 млн руб.
Кроме того, дополнительно можно рассчитать и коэффициенты эластичности 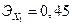 и
и  , которые показывают, что по абсолютному приросту наибольшее влияние на прибыль предприятий оказывает второй фактор: увеличение стоимости основных фондов Х2 на 1% вызывает рост прибыли на 0,55 %, тогда как рост величины оборотных средств Х1 на 1 % способствует росту прибыли на 0,45 %
, которые показывают, что по абсолютному приросту наибольшее влияние на прибыль предприятий оказывает второй фактор: увеличение стоимости основных фондов Х2 на 1% вызывает рост прибыли на 0,55 %, тогда как рост величины оборотных средств Х1 на 1 % способствует росту прибыли на 0,45 %
.
|
|
|


