 |
Применение теории игр при выработке оптимальной стратегии
|
|
|
|
Ряд задач теории игр можно преобразовать в задачи линейного программирования и решать их с помощью пакета "Поиск решения" Ехcel.
"Поиск решения" — это надстройка для Microsoft Excel, которую можно использовать для анализ "что если". С ее помощью можно найти оптимальное значение (максимум или минимум) формула, содержащейся в одной ячейке, называемой целевой, с учетом ограничений на значения в других ячейках с формулами на листе. Надстройка "Поиск решения" работает с группой ячеек, называемых ячейками переменных решения или просто ячейками переменных, которые используются при расчете формул в целевых ячейках и ячейках ограничения. Надстройка "Поиск решения" изменяет значения в ячейках переменных решения согласно пределам ячеек ограничения и выводит нужный результат в целевой ячейке.
Задача.
Определить с помощью линейного программирования решение игровой задачи вида
 .
.
Решение.
I. Если среди элементов исходной матрицы имеются отрицательные, необходимо ко всем ее элементам прибавить одно и то же положительное число γ, такое, чтобы все элементы новой матрицы были неотрицательными.
Прибавляем ко всем элементам матрицы С число γ = 1, в результате получим
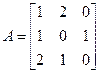
. Определяем оптимальную смешанную стратегию  игрока А.
игрока А.
1. Для этого составляем задачу линейного программирования вида

 .
.  . zi ≥ 0,
. zi ≥ 0, 
k = 1,..., n; i = 1,..., m. L = z 1 + z 2 + z 3 → min,

2. Запишем целевую функцию в виде

Введем в систему неравенств дополнительные переменные и перейдем к системе уравнений



3. Выделяем в этой системе базис z 4 z 5 z 6. Коэффициенты при базисных переменных должны быть равны единице. Для этого уравнения этой системы нужно умножить на (- 1):
|
|
|
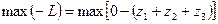

Составляем симплекс-таблицу (табл. 1):
Таблица 1
| Базис | z 1 | z 2 | z 3 | z 4 | z 5 | z 6 | Свободные члены |
| z 4 | -1 | -1 | -2 | 1 | 0 | 0 | -1 |
| z s | -2 | 0 | -1 | 0 | 1 | 0 | -1 |
| z 6 | 0 | - 1 | 0 | 0 | 0 | 1 | - 1 |
| - L | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Среди свободных членов есть отрицательные,, следовательно, используем двойственный симплекс-метод.
Выводимая из базиса переменная определяется минимальным отрицательным элементом в столбце свободных членов (выделен в таблице пунктирным овалом).
Разрешающий элемент определяется максимальным отношением небазисных элементов в строке целевой функции к соответствующим коэффициентам выводимой из базиса переменной. При этом не учитываются элементы a ij ≥ 0. Разрешающий элемент (выделен в табл. 1 сплошным овалом) находится в столбце, соответствующем переменной, вводимой в базис.
4. Далее выполняются симплекс-преобразования:
а) строка разрешающего элемента делится на разрешающий элемент;
б) из всех остальных строк таблицы вычитается полученная строка, умноженная на такие множители, чтобы во всех клетках столбца с разрешающим элементом получились нули.
Критерий оптимальности решения — положительность столбца свободных членов (кроме (- L)) (табл. 2).
Таблица 2
| Базис | z 1 | z 2 | z 3 | z 4 | z 5 | z 6 | Свободные члены |
| z 4 | -1 | 0 | -2 | 1 | 0 | -1 | 0 |
| z 1 | -2 | 0 | -1 | 0 | 1 | 0 | -1 |
| z 2 | 0 | 1 | 0 | 0 | 0 | -1 | 1 |
| -L | 1 | 0 | 1 | 0 | 0 | 1 | -1 |
Таблица 3
| Базис | z 1 | z 2 | z 3 | z 4 | z 5 | z 6 | Свободные члены |
| z 4 | 0 | 0 | -1,5 | 1 | - 0,5 | -1 | 0,5 |
| z 1 | 1 | 0 | 0,5 | 0 | - 0,5 | 0 | 0,5 |
| z 2 | 0 | 1 | 0 | 0 | 0 | -1 | 1 |
| -L | 0 | 0 | 0,5 | 0 | 0,5 | 1 | -1,5 |
Значения полученных переменных представлены в столбце свободных членов таблицы 3: z 1 = 0,5; z 2 = 1; z 3 = 0; - L = - 1,5.
Следовательно,  , а vA =
, а vA =  .
.
5. Возвращаемся к переменным х i по формулам xi = vA zi
 ;
;  ;
; 
6. Вычисляем значение цены игры для исходной матрицы по формуле

В результате получили:
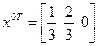 ;
; 
III. Определяем оптимальную смешанную стратегию  игрока В.
игрока В.
|
|
|
1. Составляем задачу линейного программирования вида 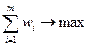 ;
; 
wk ≥ 0, i = 1, …, m; k = 1, …, n.

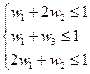
2. Запишем целевую функцию в виде

Введем в систему неравенств дополнительные переменные и перейдем к системе уравнений
 ;
;

3. Составляем симплекс-таблицу (табл. 4).
Таблица 4
| Базис | w 1 | w 2 | w 3 | w 4 | w 5 | w 6 | Свободные члены |
| w 4 | 1 | 2 | 0 | 1 | 0 | 0 | 1 |
| w 5 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| w 6 | 2 | 1 | 0 | 0 | 0 | 1 | 1 |
| L' | -1 | -1 | -1 | 0 | 0 | 0 | 0 |
Свободные члены положительны, поэтому применяем прямой симплекс-метод.
Вводимая в базис переменная определяется минимальным отрицательным элементом в строке целевой функции (выделен в табл. 4 пунктирным овалом), знак свободного члена при этом не учитывается.
Разрешающий элемент определяется минимальным из отношений свободных членов к соответствующим коэффициентам при выбранной вводимой в базис переменной (не учитываются элементы а ij ≤ 0). Разрешающий элемент (выделен в таблице сплошным овалом) находится в строке, соответствующей переменной, выводимой из базиса.
4. Далее выполняются симплекс-преобразования (табл. 5—6).
Признак оптимальности решения — неотрицательность всех элементов в строке целевой функции.
Таблица 5
| Базис | w 1 | w 2 | w 3 | w 4 | w 5 | w 6 | Свободные члены |
| w 4 | 1 | 2 | 0 | 1 | 0 | 0 | 1 |
| w 3 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| w 6 | 2 | 1 | 0 | 0 | 0 | 1 | 1 |
| L' | 0 | -1 | 0 | 0 | 1 | 0 | 1 |
Таблица 6
| Базис | w 1 | w 2 | w 3 | w 4 | w 5 | w 6 | Свободные члены |
| w 2 | 0,5 | 1 | 0 | 0,5 | 0 | 0 | 0,5 |
| w 3 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| w 6 | 1,5 | 0 | 0 | -0,5 | 0 | 1 | 0,5 |
| L' | 0,5 | 0 | 0 | 0,5 | 1 | 0 | 1,5 |
Значения полученных переменных представлены в столбце свободных членов таблицы 1.7: w 1 = 0; w 2 = 0,5; w 1 = 1;  , следовательно, vA =
, следовательно, vA =  .
.
5. Возвращаемся к переменному yi по формулам yi = vA wi:
 ;
;  ;
; 
6. Вычисляем цену игры для исходной матрицы:

Ответ:  ;
;  ;
; 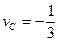 .
.
ПР№5.Риски в проектах
|
|
|


