Элементарные вычисления в системе Maple

Элементарные вычисления в системе Maple

Числа и константы

Если в выражении встречается число, записанное с плавающей точкой (например, 3. 14 или 5. 6e-17), то все вычисления выполняются приближенно, в противном случае вычисления проводятся точно.

В Maple есть следующие константы:

Pi

число π (=3. 141592653589793238…)

 

I

мнимая единица i (i² = -1)

 

exp(1)

основание натуральных логарифмов e

 

infinity

бесконечность

 

true

логическая истина

 

false

логическая ложь

Вычисления с участием констант выполняются точно (если только их значение не будет переведено к действительному значению), например:

> sin(Pi/3); 3^1/2/2

> sin(Pi);

0

> sin(3. 1415926);

 

0. 5358979324 10^-7

Операторы

В Maple существуют следующие операторы:

Арифметические: +, -, *, /, ^ (возведение в степень), ! (факториал).

Логические: <, >, > =, < =, = (равно), < > (не равно).

Оператор присваивания: : =.

Переменные

Переменной может являться любой идентификатор, состоящий из английских букв и цифр, начинающийся с буквы и являющийся уникальным (т. е. не совпадающий ни с одним из зарезервированных слов! ).

Переменной может быть присвоено любое значение при помощи оператора присваивания: =. Переменная, которой не присвоено никакое значение считается свободной переменной и ее имя сохраняется в арифметических вычислениях.

Например:

> a: =2: b: =3: > (a+b)^2; 25

> (a+c)^2;

 

(2+c)²

Стандартные функции

x^1/2 – sqrt(x)

|x| – abs(x)

Знак x (возвращает 1, -1 или 0) – sign(x)

Тригонометрические функции – sin(x), cos(x), tan(x), cot(x)

Обратные тригонометрические – arcsin(x), arccos(x), arctan(x), arccot(x)

Экспонента – exp(x)

Натуральный, десятичный логарифм и логарифм по данному основанию a – ln(x), log10(x), log[a](x).

Пример:

> y: =log[a](x);

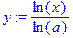
> y: =log[2](x);

> y: =log[1](x);

Error, (in log[1]) numeric exception: division by zero

В последнем случае нами преднамеренно была нарушена область определения логарифмической функции, на что немедленно указала система Maple.

Преобразование математических выражений

В выражение могут входить константы, свободные переменные, математические функции.

Пример выражения:

> A: =sin(sqrt(Pi)+exp(2));

Довольно часто в качестве выражений выступают многочлены от одной или нескольких переменных или рациональные выражения. Maple содержит различные функции для преобразования таких выражений.

Функция factor(eq) разлагает выражение eq на множители.

> P: =x^4+2*x^3+2*x^2+2*x+1: > factor(P); (x²+1)(x+1)²

Функция expand(eq) раскрывает скобки в выражении. Если указать один или несколько дополнительных параметров в виде expand(eq, a, b, c), то выражения a, b, c раскрываться не будут. Это полезно, если необходимо каждое слагаемое умножить на какое-то выражение.

Примеры:

> expand((x+1)*(x+2)); x²+3x+2

> expand(sin(x+y));

sin(x)cos(y)+cos(x)sin(y)

> expand((x+1)*(y+z), x+1);

 

(x+1)y+(x+1)z

Для приведения дробей к общему знаменателю с последующим сокращением используется функция normal(eq).

> normal(1/x+1/y);

> (a^4-b^4)/((a^2+b^2)*a*b);

 

> normal(%);

Функция simplify(eq) упрощает выражение eq. В качестве второго (необязательного) параметра, ей можно указать, какие выражения преобразовывать:

trig – тригонометрические,

power – степенные,

radical – радикалы,

exp – экспоненты,

ln – логарифмы.

Пример:

> simplify(sin(x)^2+cos(x)^2);

Решение уравнений

Обыкновенные (алгебраические) уравнения

Для решения уравнений используется функция solve(eq, x), где eq – решаемое уравнение, x – имя переменной, относительно которой разрешается уравнение. Пример:

> solve(x^2+x-1=0, x);

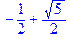
> solve(a*x+b=0, x);

> solve(a*x+b=0, b);

Если уравнение имеет несколько решений, то в этом случае решение уравнения можно присвоить некоторой переменной, например, обозначим ее как p.

Далее можно использовать k-е решение уравнения в виде p[k]:

> p: =solve(x^2+x-1=0, x): p[1];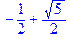

> simplify(p[1]*p[2]);

-1

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: