Проверка чисел на простоту, разложение на множители и построение простых чисел

Проверка чисел на простоту, разложение на множители и построение простых чисел

Для проверки числа на простоту используется функция isprime, которая возвращает true, если число простое и false – если составное. Для разложения числа на множители используются функции ifactor и ifactors. Первая функция возвращает результат в виде произведения степеней простых чисел, вторая – в виде списка простых чисел и их степеней. Все эти функции работают значительно эффективней простого подбора делителей, проверка на простоту осуществляется быстрее полного разложения на множители.

Для построения простых чисел используются функции prevprime, nextprime, ithprime. Функция prevprime(n) возвращает наибольшее простое число, которое меньше n, функция nextprime(n) возвращает наименьшее простое число, которое больше n. Функция ithprime(n) возвращает n-е простое число.

Для нахождения случайного простого числа следует использовать эти функции вместе с функцией rand(), которая возвращает псевдослучайное 12-значное натуральное число. Для инициализации генератора псевдослучайных чисел необходимо использовать функцию randomize().

> isprime(7! ); false

> ifactor(7! );

> ifactors(7! );

[1, [[2, 4], [3, 2], [5, 1], [7, 1]]]

> nexprime(7! );

5051

> isprime(%);

true

> nextprime(rand());

427419669163

Решение диофантовых уравнений

Для решения уравнений в целых числах используется функция isolve.

Примеры:

> isolve(5*x+7*y=1);

В данном случае _Z1 обозначает произвольное целое число, т. к. общее решение этого уравнения имеет вид x=-4-7∙ n, y=3+5∙ n.

Используем функцию isolve для решения уравнения Пелля x²-2y²=1.

Это уравнение имеет 4 серии решений, отличающиеся только знаками.

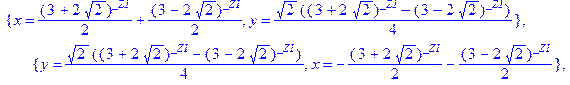
Положительные решения уравнения содержатся в первой строке приведенных формул (решения определены через целый параметр _Z1).

Приведем теперь следующую последовательность команд:

> sol: =isolve(x^2-2*y^2=1):

Положим далее _Z1=0 и вычислим решение:

> _Z1: =0: sol;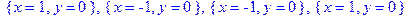

Это – тривиальное решение.

Минимальное нетривиальное решение будет при _Z1=1:

> _Z1: =1: sol;

При _Z1=2 решение, полученное системой Maple, будет содержать знаки радикалов, вследствие чего необходимо использовать функцию expand для их раскрытия:

> _Z1: =2: expand(sol);

Для того, чтобы отменить уже имеющееся присвоение переменной _Z1 конкретного значения и снова сделать ее свободной (неопределенной) переменной, необходимо использовать функцию unassign('_Z1'); .

Самостоятельные упражнения

1. Разложить на множители число 10¹⁰+1.
2. Проверить, является ли число 10¹⁰⁰+1 простым.
3. Найти наибольший общий делитель чисел 10¹⁰+1 и 10¹⁸+1.
4. Найти общий вид решения в целых числах уравнения 3x+5y=179.
5. Найти общий вид решения в натуральных числах уравнения x²-2y²=-1. Найти первых три наименьших его решения.

 

⇐ Предыдущая123456

Поделиться:

Воспользуйтесь поиском по сайту: