Системы уравнений. Численное решение уравнений. Решение тригонометрических уравнений. Самостоятельные упражнения. Тема 2. Применение Maple в математическом анализе

Системы уравнений

Системы уравнений решаются с помощью такой же функции solve({eq1, eq2,... }, {x1, x2,... }), только теперь в параметрах функции следует указывать в первых фигурных скобках через запятую уравнения, а во вторых фигурных скобках перечисляются через запятую переменные, относительно которых требуется решить систему. Если необходимо использовать полученные решения уравнений для дальнейших вычислений, то необходимо результат, возвращаемый функцией solve присвоить какой-нибудь переменной, например, p, а затем выполнить команду assign(p).

Пример:

> p: =solve( {x+y=a, x-y=b}, {x, y} ): > assign(p); > x; a/2+b/2

Численное решение уравнений

Попробуем решить уравнение: x⁶-2x+1=0. Использование функции solve даст нам один корень, равный 1, и еще набор выражений вида RootOf(_Z^5+_Z^4+_Z^3+_Z^2+_Z-1, index = 1). Дело в том, что произвольное уравнение степени выше 4 с рациональными коэффициентами может не иметь корней, выразимых в виде радикалов над рациональными числами. Решения всевозможных таких уравнений называются алгебраическими числами. Данное уравнение также неразрешимо в радикалах, и Maple нашла нам единственный корень, выразимый в радикалах (=1) и сообщила, что оставшиеся корни являются алгебраическими числами: корнями многочлена z⁵+z⁴+z³+z²+z-1=0 (именно этот многочлен указан в аргументе функции RootOf).

Maple умеет работать с алгебраическими числами, но можно также найти приближенное численное решение при помощи функции fsolve:

> fsolve(x^6-2*x+1=0, x); 0. 5086603916, 1. 000000000 > y: =(x-10000)*(x+9888. 9);

> expand(y);

> fsolve(y=0, x); -9888. 900000, 10000. > fsolve(y=10, x); -9888. 900503, 10000. 00050

Иногда Maple при решении трансцендентных уравнений не выводит сложные выражения в виде радикалов, а оставляет их в форме RootOf. Чтобы заставить Maple выводить все решения в виде радикалов (естественно, если они представимы в такой форме), необходимо присвоить значение true системной переменной _EnvExplicit(_EnvExplicit: =true); .

 

Решение тригонометрических уравнений

Команда solve, применяемая для решения тригонометрических уравнений, находит только главные решения, то есть выводит только одно решение из серии периодических решений:

> solve(sin(2*x)+cos(2*x)=1, x);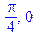

Для того, чтобы система Maple находила все решения, необходимо предварительно присвоить значение true системной переменной _EnvAllSolutions. Тогда мы получим результат в другом виде, в котором будут фигурировать переменные Z1~ и Z2~. Эти переменные обозначают произвольную константу целого типа, в более привычном виде решения можно будет записать, как π /4+π n, π k.

Самостоятельные упражнения

1. Вычислить значение (6+2∙ 5^1/2)^1/2-(6-2∙ 5^1/2)^1/2.
2. Вычислить sin⁴(π /8)+cos⁴(3π /8)+sin⁴(5π /8)+cos⁴(7π /8).
3. Упростить выражение (1 + sin(2x) + cos(2x))/(1 + sin(2x) - cos(2x)).
4. Разложить на множители многочлен x³-4x²+5x-2.
5. Найти численное решение тригонометрического уравнения cos x = x.
6. Решить уравнение 3x-(18x+1)^1/2+1=0.
7. Решить уравнение ||2x-3|-1|=x.
8. Решить тригонометрическое уравнение (найди все решения! ) sin x - cos x=1/sin x.
9. Решить систему алгебраических уравнений:

 

Тема 2. Применение Maple в математическом анализе

Стандартная библиотека

Большинство команд, выполняющих основные математические операции - интегрирование, дифференцирование, разложение в ряды, суммирование и т. п. - находится в стандартной библиотеке Maple, т. е. доступно без предварительного указания имени библиотеки.

Мнемоника этих команд и назначение параметров отражают их математический смысл и не требуют дополнительных пояснений. В данном пособии приводятся наиболее употребимые в задачах математического моделирования команды.

Список некоторых команд из стандартной библиотеки для удобства пользования приведем в алфавитном порядке.

array(1.. n, list) Создает вектор (одномерный массив) из n элементов списка list.

asympt(expr, var) Вычисляет асимптотическое разложение по переменной var выражения expr относительно бесконечности.

chebyshev(expr, var=a.. b) Вычисляет Чебышевское разложение выражения expr по переменной var на интервале [a.. b].

coeftayl(expr, var=a, n) Вычисляет коэффициент при члене степени n для разложения в ряд Тейлора выражения expr по переменной var в точке a.

conjugate(cmplx) Вычисляет комплексно-сопряженное для комплексной величины cmplx.

convert(list, array) Переводит список list в одномерный массив array с теми же элементами.

convert(list, vector) Переводит список list в вектор vector с теми же элементами.

convert(list1,..., listn, matrix) Переводит списки list1,..., listn в матрицу.

convert(s, poly) Преобразует список s в полином poly.

convert(s, ratpoly) Преобразует список s в полиномиальное выражение.

convert(poly, series) Преобразует полином poly в список series.

copy(M) Создает копию массива M ( матрицы или вектора).

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: