Парные, частные коэффициенты корреляции, совокупные коэффициенты множественной корреляции и детерминации. Понятие и связь между ними.

Если факторные признаки различны по своей сущно­сти и/или имеют различные единицы измерения, то коэф­фициенты регрессии при разных факторах являются не­сопоставимыми. Поэтому уравнение регрессии дополняют соизмеримыми показателями тесноты связи фактора с ре­зультатом, позволяющими ранжировать факторы. К ним от­носят: частные коэффициенты эластичности, β -коэффициенты, частные коэффициенты корреляции.

Парные коэффициенты корреляции. Для измерения тесноты связи между двумя из рассматриваемых переменных (без учета их взаимодействия с другими переменными) применяются парные коэффициенты корреляции. Методика расчета таких коэффициентов и их интерпретации аналогичны линейному коэффициенту корреляции в случае однофакторной связи.

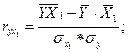
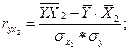
где 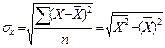- среднее квадратическое отклонение факторного признака;

- среднее квадратическое отклонение результативного признака.

Коэффициент частной корреляции измеряет тесноту линейной связи между отдельным фактором и результатом при устранении воздействия прочих факторов модели.

Для качественной оценки тесноты связи можно использовать следующую классификацию:

0.1- 0.3- слабая связь

0.3-0.5 – умеренная связь

0.5-0.7- заметная связь

0.7-0.9- тесная связь

0.9-0.99- весьма тесная

Для расчета частных коэффициентов корреляции мо­гут быть использованы парные коэффициенты корреляции.

Для случая зависимости Yот двух факторов можно вычислить 2 коэффициента частной корреляции:

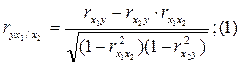
(2-ой фактор 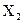фиксирован);

 

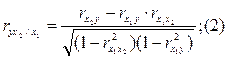
(1-ый фактор 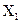фиксирован).

 

Это коэффициенты частной корреляции 1-ого порядка (порядок определяется числом факторов, влияние которых на результат устраняется).

Частные коэффициенты корреляции, рассчитанные по таким формулам изменяются от -1 до +1. Они используют­ся не только для ранжирования факторов модели по степени влияния на результат, но и также для отсева факторов. При малых значениях 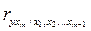нет смысла вводить в уравнение m -ый фактор, т.к. качество уравнения регрессии при его введении возрастет незначительно (т.е. теоретиче­ский коэффициент детерминации увеличится незначитель­но).

Совокупный коэффициент множественной корреляции или индекс множественной корреляции определяет тесноту совместного влияния факторов на результат:

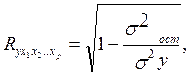
где 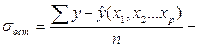остаточная дисперсия;

или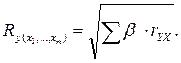

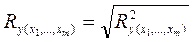. Он принимает значения от 0 до 1 (в отличие от парного коэффициента корреляции, который может прини­мать отрицательные значения, R используется без учета на­правления связи). Чем плотнее фактические значения 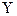располагаются относительно линии регрессии, тем меньше остаточная дисперсия и, следовательно, больше величина 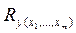. Таким образом, при значении R близком к 1, урав­нение регрессии лучше описывает фактические данные и факторы сильнее влияют на результат; при значении R близком к 0 уравнение регрессии плохо описывает фактиче­ские данные и факторы оказывают слабое воздействие на результат.

При трех переменных для двух факторного уравнения регрессии данная формула совокупного коэффициента множественной корреляции легко приводится к следующему виду:

Чем R ближе к единице, тем совокупное влияние изучаемых показателей x₁ и x₂ на результативный фактор y больше (корреляционная связь более интенсивная).

Множественный (совокупный) коэффициент детерминации определим как квадрат множественного коэффициента корреляции. Показывает, какая доля вариации изучаемого показателя объясняется влиянием факторов, включенных в уравнение множественной регрессии. Его значение - в пределах от нуля до единицы. Чем ближе множественный коэффициент детерминации к единице, тем вариация изучаемого показателя в большей мере характеризуется влиянием отобранных факторов.

Связь: Частный коэффициент корреляции в отличие от коэффициента (полного) парной корреляции между явлениями показывает тесноту связи после устранения изменений, обусловленных влиянием третьего явления на оба коррелируемых признака (из значений корреляционных признаков вычитаются линейные оценки в связи с третьим признаком).

Также из приведенных ранее формул частных коэффициентов корреляции видна связь этих показателей с совокупным коэффициентом корреляции. Зная частные коэффициенты корреляции (последовательно первого, второго и более высокого порядка), можно определить совокупный коэффициент корреляции по формуле:

При полной зависимости результативного признака от исследуемых факторов коэффициент совокупного их влияния равен единице. Из единицы вычитается доля остаточной дисперсии результативного признака 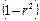, обусловленная последовательно включенными в анализ факторами. В результате подкоренное выражение характеризует совокупное действие всех исследуемых факторов.

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: