 |
A 1.1. Оптические волны в вакууме
|
|
|
|
Оптическими волнами в вакууме являются на самом деле электромагнитные волны, являющиеся решением дифференциального уравнения распространения, производные от уравнений Максвелла в вакууме:
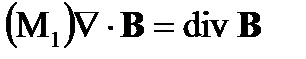(нет свободных «магнитных зарядов») (A1.1)
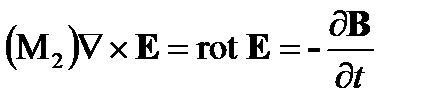(Закон Фарадея- Максвелла) (A1.2)
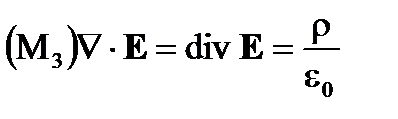(Закон Максвелла-Гаусса) (A1.3)
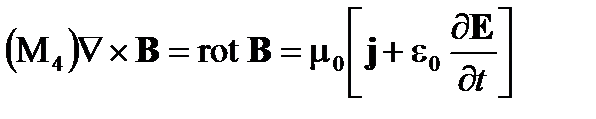(Закон Максвелла-Ампера)(А1.4)
где E – вектор электрического поля, В – вектор является магнитного поля, j –вектор плотности электрического тока, ρ – плотность электрических зарядов, ε0 – диэлектрическая проницаемость вакуума (ε0 = 8,854×10–12 Ф/м) и µ0 – магнитная проницаемость вакуума (µ0 = 4π×10–7 Гн/м).
Обратите внимание, что уравнения сохранения полного заряда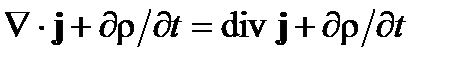 
включается в уравнения Максвелла, поскольку оно может быть получено путем применения 
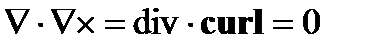к закону Максвелла-Ампера M4. Кроме того, уравнения М1 и M2 выражают, что поля E и В являются производными от электромагнитного скалярного потенциала V и электромагнитного вектора потенциала A:
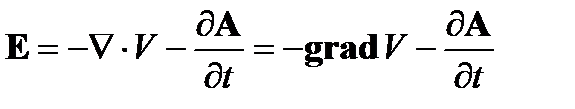(A1.5)
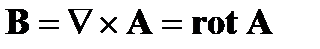(A1.6)
Эти уравнения используют дивергенцию (div) и ротор (rot) операторов векторной функции U пространственных координат, а также оператора градиента (grad) от скалярной функции U. Обозначения могут быть объединены с оператором дифференциала вектора 
, дивергенция, скалярное произведение 
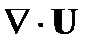, которая дает скалярную функцию, ротор, будучи векторным произведением 
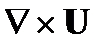, дает векторную функцию и градиент, будучи произведением векторного оператора 
со скаляром U, который представляет векторную функцию.
Другой оператор, оператор Лапласа, имеет важное значение в векторном анализ: это скалярный дифференциальный оператор, равный скалярной площади от векторного оператора 
(обозначаемый 
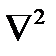), применяется в векторной функции U. Это дает вектор функции 
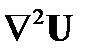. В декартовых координатах
|
|
|
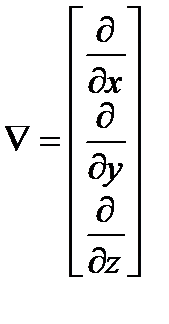
(A1.7)
Уравнение распространения выводится из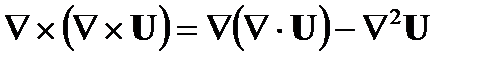 
или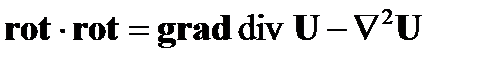 
в вакууме без источников (j = 0, ρ = 0):
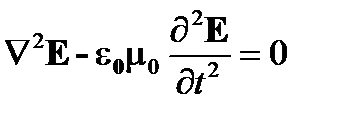
(A1.8)
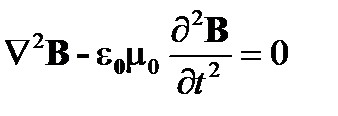
Простое решение для этих уравнений распространения является монохроматической (т.е. одной частоты) синусоидальной плоской волной, которое может быть выражено в декартовых координатах (x, y, z и времени t) (Рисунок A1.1). Для упрощения расчетов используем комплексное экспоненциальное обозначение, но необходимо иметь в виду, что это верно только для реальной части.
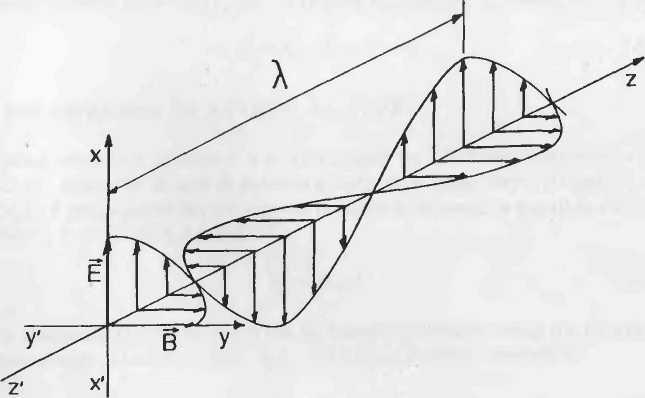
| Рисунок A l.l. Монохроматическая электромагнитная плоская волна |
,
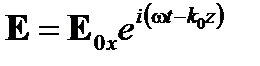(A1.9)
,
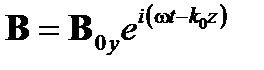где ω – циклическая частота и k 0 – волновое число в вакууме. В направлении z электромагнитное поле синусоидально колеблется с частотой f; с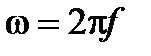 
. На данный момент времени t, электромагнитное поле имеет синусоидальной пространственного распределения вдоль оси распространения z с пространственным периодом под названием длина волны в вакууме λ; с 
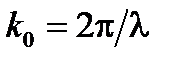. Обратное от длины волны λ называется пространственной частотой и обозначается σ.
Волна распространяет со скоростью с в вакууме, поэтому можно записать
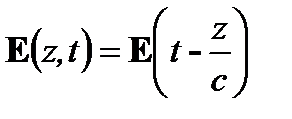
(Al.10)
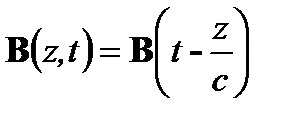
с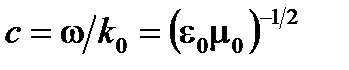 
. Ее измеренное значение с = 2,998×108 м/с и 
.
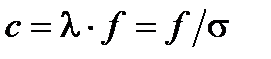Электромагнитная плоская волна в вакууме является поперечной волной, в которой E и В поля ортогональны в направлении распространения. Амплитуды полей E и В пропорциональны, и их соотношение равно скорости света:
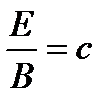(Al.11)
Они колеблются в фазе и локализованы в двух ортогональных плоскостях. Электромагнитное поле имеет то же значение в любой точке в плоскости, перпендикулярной оси распространения. Такие плоскости называются планарными волновыми фронтами.
Это постоянное соотношение E/В=c означает, что эффект электромагнитного поля – электромагнитные волны возникают главным образом благодаря электрическому компоненту. Электромагнитная сила f EM применительно к частицам заряда q является суммой электрической силы f Е и магнитной силы f M:
|
|
|
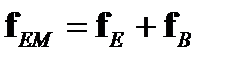
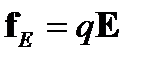(A1.12)
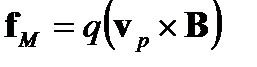
где v p – скорость частицы. Поскольку на самом деле v p << c, это означает, что fM << fE. Итак, большинство проблем электромагнитных волн рассматриваются только с электрическим полем.
Электромагнитный спектр простирается от радиоволн до гамма-излучения: оптические волны соответствуют видимому диапазону (например, в вакууме длине волны между 400 и 750 нм) и недалеко от ультрафиолета и ближнего инфракрасного диапазонов. Важной характеристикой этих оптических волн является их очень высокая частота: для вакуумной длины волны λ 1 мкм частота волны f =3×1014 Гц или 300.000 ГГц! Электронная система не может следовать такой быстрой вибрации, и оптические датчики могут измерять только среднюю мощность волны. Невозможно измерить непосредственно поле E или В волны.
Мощность потока через единицу поверхности называется интенсивностью I волны, она пропорциональна среднему значению площади скалярного поля E:
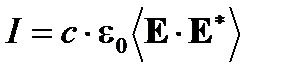(A1.13)
где E* –комплексная сопряженная E и скобки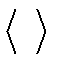 
обозначают усреднение по времени. Оптические датчики часто называют по закону квадрата или квадратические детекторы.
Когда не требуется точный физический или векторный характер оптической волны, анализ оптической схемы может осуществляться со скалярной величиной, комплексной волной с амплитудой A 0:
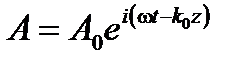(A1.14)
Интенсивность волны – это среднее значение скалярной площади комплексной амплитуды:
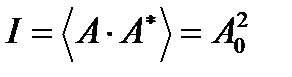(A1.15)
|
|
|
