 |
A1.2. Поляризация оптических волн
|
|
|
|
Оптические волны в вакууме это волны, обозначаемые ПЕМ (переносимые электромагнитные), поскольку поля E и В оба в плоскости 0 xy ортогональны направлению распространения 0 z. Принимая за начало координат 0, получим одно из возможных пространственных решений электрического поля (Рисунок A1.2)
(A1.16)
| Рисунок A1.2. Линейная поляризация вдоль осей x или y |
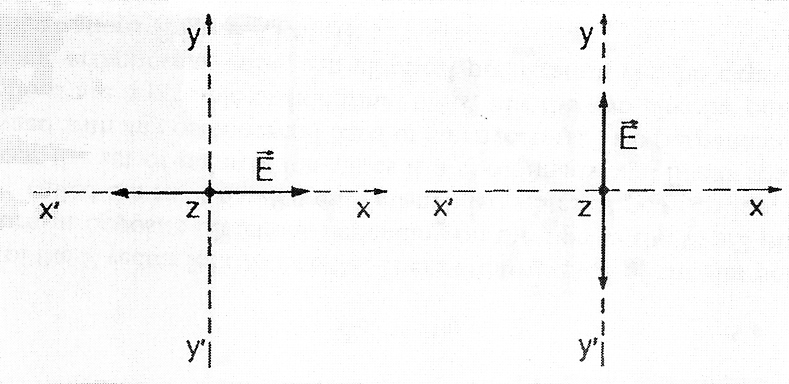
Считается, что такие синусоидальные колебания должны быть линейно поляризованными вдоль оси 0 x. Вектор E всегда остается параллельным E 0 x. Другим возможным решением является
(A1.17)
Затем волна линейно поляризована вдоль перпендикуляра оси 0y.
Набором всех возможных решений является двухмерное линейное пространство с комплексным коэффициентом. Общее решение является линейной комбинации с комплексными коэффициентами:
(А1.18)
где 
– разность фаз между обеими ортогональными компонентами E 0 x и E 0 y.
Когда равен 0 или π рад, волна линейно поляризована в промежуточном направлении (рис. А1.3), но в целом волна является эллиптически поляризованной. Конец вектора E вектора следует по эллипсу с частотой 
(Рисунок. Al.4). Когда две линейные поляризации с теми же амплитудами объединяются в квадратуру (т.е. с фазовый сдвиг ± π/2 рад), результатом является круговая поляризация (Рисунок. A1.5):
| Линейный |
| + |
|
|
| Рисунок A1.3. Линейная поляризация выровнена по любой оси |
|
| + |
| еiΔΦ |
| Эллиптическая |
| Рисунок A l.4. Эллиптическая поляризация, рассматриваемая как сумма двух линейных поляризаций |
(A1.19)
где амплитуды векторов E 0 x и E 0 y равны:
E 0 x = E 0 y.
Кончик вектора E следует по кругу. Есть два состояния круговой поляризации, которые переключаются в противоположных направлениях в зависимости от знака ±π/2 фазового сдвига. Они называются право-ручным и лево-ручным состояниями поляризации.
|
|
|
| + |
| еiπ/2 |
| Круговая |
|
| Рисунок A l.5. Круговая поляризация |
Так как набор состояний поляризации в двумерном линейном пространстве, он может быть проанализирован в ортонормальном базисе собственных векторов. Две перпендикулярные линейные поляризации являются возможной основой ортонормального базиса, но две круговые поляризации также имеют ортонормальный базис. Эллиптические поляризации могут быть выражены линейными поляризациями (Рисунок A1.6(a)):
(A1.20)
где Е 0 L – пиковое значение поля вдоль большой оси, и Е 0 s – пиковое значение поля вдоль малой оси. Тем не менее, оно также может быть разложено с круговой поляризацией (Рисунок A1.6(b)):
(A1.21)
|
|
(A1.22)
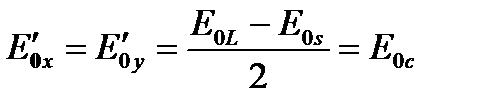(A1.23)
с E 0 m > E 0 c, и где E 0 m – амплитуда основного кругового компонента вращающегося поля E m и E 0 c – амплитуда другого пересекающего кругового компонента вращающегося поля E с. Итак,
(A1.24)
(A 1.25)
| Рисунок A1.6. Разложение эллиптической поляризации: (a) с двумя линейными поляризациями в квадратуре; (b) с двумя круговыми поляризациями |
| Эллиптическая |
| Линейная |
| Круговая |
Примечание: Когда данное качество состояния поляризации должно измеряться, отношение интенсивностей измеряется между компонентами, в которых даны состояния поляризации и компонентами в состоянии ортогональной поляризации.
С состоянием линейной поляризации поляризатор используется для выбора основных компонент поляризации, и он поворачивается на 90 град для выбора скрещенных ортогональных поляризаций. Соотношение между обеими измеренными мощностями непосредственно дает соотношение между интенсивностью Iс скрещенного линейной состояния и интенсивностью Im основного линейного состояния.
|
|
|
В состоянии круговой поляризации поляризатор используется для проверки, что передаваемая мощность при повороте поляризатора остается равной половине входной мощности. Когда циркулярное состояние не совершенно, максимальная мощность P max измеряется вдоль мажорной оси поляризации, которая не вполне циркулярна, и минимальная мощность P min измеряется вдоль минорной оси. P max на самом деле является мощностью линейной E 0 L компоненты эллиптической поляризации и она пропорциональна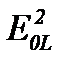 
, а P min –мощность E 0 s и пропорциональна 
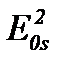. Коэффициент поляризации этих вариантов
(A1.26)
и поскольку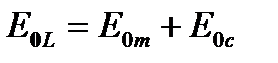 
, 
и 
,
, (A1.27)
где Im сейчас интенсивность главного кругового состояния, а Iс – интенсивность перекрестного кругового состояния. Затем этот вариант коэффициента поляризации пропорционален отношению амплитуд (или полей) обоих ортогональных циркулярных компонентов; то есть квадратному корню из отношений интенсивностей (или мощностей).
Если, например, отношение Iс/Im = 1%, коэффициент поляризации достигает 20%. Это не означает, что это основное состояние круговой поляризации также не сохраняется, как состояние основных линейной поляризации в предыдущем случае. В обоих случаях отношение интенсивностей или мощностей определяется как Iс/Im и отношение амплитуд полей составляет 
; но в линейном случае эксперимент измеряет отношение интенсивностей при дефектах, несмотря на то, что в циркулярном случае эксперимент дает измерения отношения амплитуд, которое является гораздо более чувствительным!
|
|
|
