 |
A1.3. Распространение в диэлектрической среде
|
|
|
|
В среде уравнения Максвелла могут усредняться пространственно для устранения сильных колебаний электромагнитного поля между дискретными заряженными частицами материала и имеют возможность описывать макроскопически непрерывный материал. Первые два уравнения Максвелла уравнения М1 и M2, которые не зависят от ρ и j, сохраняются в среднем:
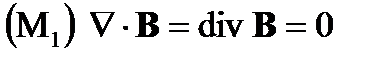 (A1.28)
(A1.28)
 (A1.29)
(A1.29)
Макроскопический эффект заряда среды может приниматься во внимание вектором электрической поляризации P и вектором магнитной поляризация M (Обратите внимание, что "поляризации" в данном случае полностью отличается по значению от "состояния поляризации"). Производная электрического поля D и производная магнитного поля Н могут быть определены следующим:
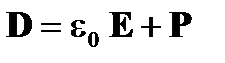 (A 1.30)
(A 1.30)
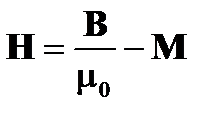 (A1.31)
(A1.31)
 (A1.32)
(A1.32)
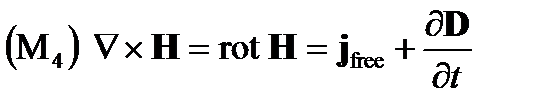 (A1.33)
(A1.33)
где ρfrее – плотность свободных зарядов и j frее – вектор свободной плотности тока.
В изотропной линейной диэлектрической (т.е. непроводящей) среде ρfrее= 0, j frее = 0, P пропорциональна E, и M пропорциональна B:
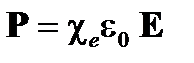 (A1.34)
(A1.34)
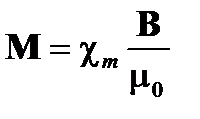 (A1.35)
(A1.35)
где 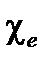 и
и 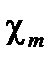 – соответственно диэлектрическая и магнитная восприимчивости. Производные полей D и H также соответственно пропорциональны полям E и В:
– соответственно диэлектрическая и магнитная восприимчивости. Производные полей D и H также соответственно пропорциональны полям E и В:
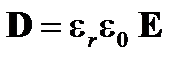 (A1.36)
(A1.36)
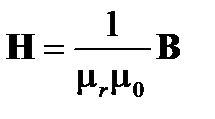 (A1.37)
(A1.37)
где ε r – относительная диэлектрическая проницаемость и μ r – относительная магнитная проницаемость. У нас есть
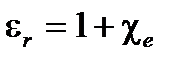 (A1.38)
(A1.38)
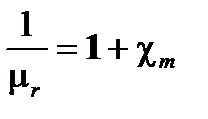 (A1.39)
(A1.39)
Заметим, что 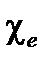 ,
, 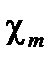 , ε r и μ r безразмерные величины.
, ε r и μ r безразмерные величины.
Уравнение распространения становится
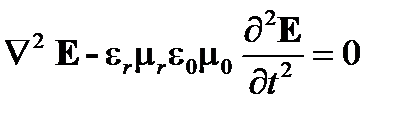
(A1.40)
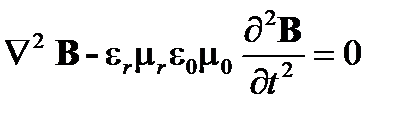
Имеем решение плоской волны
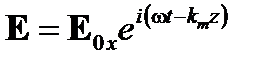
(A1.41)
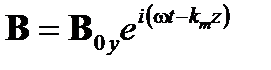
Скорость волны 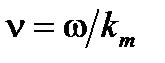 в среде имеет вид
в среде имеет вид
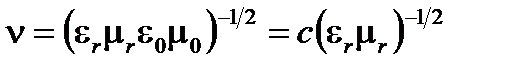 (A1.42)
(A1.42)
Показатель преломления n материала определяется соотношением скорости в вакууме и скорости в среде:
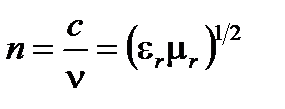 (A1.43)
(A1.43)
Даже если это может показаться очевидным, важно напомнить, что, когда световая волна распространяет в вакууме и в различных средах, ее временнáя частота f и ее соответствующая угловая частота ω=2π f остаются неизменными; но фактическая пространственная частота σ m и ее обратное значение, фактическая длина волны λ m в среде не равны больше значениям σ и λ, которые эта волна будет иметь в вакууме. Имеем
|
|
|
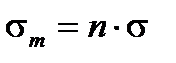 (A1.44)
(A1.44)
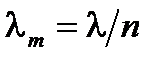 (A1.45)
(A1.45)
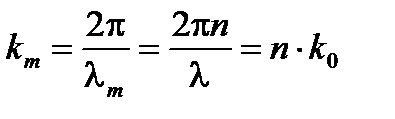 (A1.46)
(A1.46)
где k 0 является волновым числом, тем же, что и в вакууме.
Как видно, важной характеристикой пучка света, которая остается инвариантной, является ее временнáя частота, даже если это привычка дать ее длину волны в вакууме, потому что длину 1 мкм легче понять количество, измерять, чем частоту 300,000 ГГц или время 3 фемтосекунды.
Обратите внимание, что относительная диэлектрическая проницаемость ε r зависит от частоты волны, а относительная магнитная проницаемость μ r на частотах оптических волн равна единице. Тогда показатель преломления и скорость волны зависят только от ε r и частота (или длина волны) зависят:
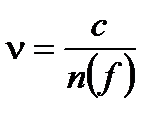
(A1.47)
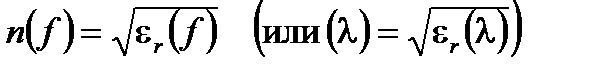
Фактически материал состоит из электрических частиц, которые связаны вместе электромагнитными силами. Он может считаться сложным набором эластичных механических осцилляторов. Когда частоты света соответствуют резонансной частоте материала, синхронизированным электромагнитным полем волны вызывается механический резонанс, который затем поглощается. В диапазоне прозрачного света частоты не соответствуют любому резонансу, но вызывают вибрацию осцилляторов и макроскопический эффект, описываемый ε r, зависящем от соответствующего значения частоты света и резонансных частот материала, это учитывается частотной зависимостью ε r и показателя преломления n.
Этот эффект называется хроматической дисперсией, поскольку ее первое применения известно из пространственного разложения белого света в цвета после прохождения призмы. Белый свет состоит из всевозможных видимых длин волн, и поскольку угловое отклонение призмы пропорционально показателю преломления n, спектра становится распространяющимся под углом, зависящим от функций n (f) (или n (λ)).
|
|
|
Дисперсия дает два других важных явления. Если оптические волны модулируются по амплитуде, частоте или фазе, модулированный "сигнал" распространяется не со скоростью 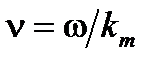 , часто называемой фазовой скоростью, а с так называемой групповой скоростью vg, пропорциональной производной первого порядка d n /dλ.
, часто называемой фазовой скоростью, а с так называемой групповой скоростью vg, пропорциональной производной первого порядка d n /dλ.

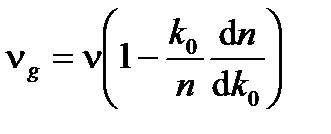 (A1.48)
(A1.48)
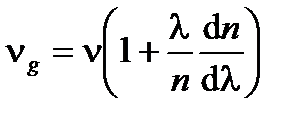
Любаянемонохроматическая является суммирования компонентов всех ее частот. С этих пространственных позиций волна с амплитудой A (t)
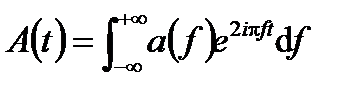 (A1.49)
(A1.49)
Ее частотные компоненты a (f) определяются обратным преобразованием Фурье:
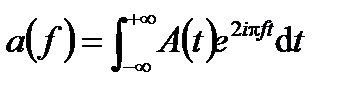 (A1.50)
(A1.50)
Использование угловой частоты ω вместо временной частоты f дает
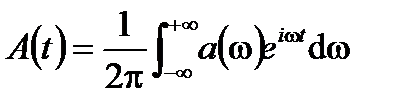 (A1.51)
(A1.51)
Когда эта волна распространяется в дисперсной среде, каждый компонент частоты распространяется самостоятельно со своей собственной скоростью и общей амплитудой волны A (t,z) в соответствии
 (A1.52)
(A1.52)
Аргумент переноса 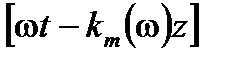 может быть представлен суммой усредненных членов
может быть представлен суммой усредненных членов 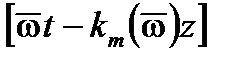 , которые зависят от средней частоты
, которые зависят от средней частоты  и переменных членов
и переменных членов  , где
, где 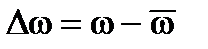 и
и  . Амплитуда волны становится
. Амплитуда волны становится
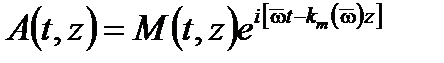 (A1.53)
(A1.53)
Второй член имеет тот же аргумент распространения, что и первый в монохроматической волне и представляет распространение носителя со скоростью, равной средней фазовой скорости 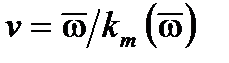 . Первый член
. Первый член  является на самом деле модуляцией, которая распространяется монохроматическим носителем, и
является на самом деле модуляцией, которая распространяется монохроматическим носителем, и
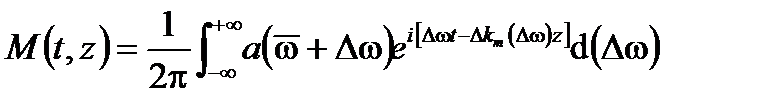 (А1.54)
(А1.54)
Термин модуляции M (t,z) является неотъемлемой частью интегралом суммирования компонентов частоты 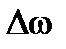 , которые распространяются соответственно со скоростью
, которые распространяются соответственно со скоростью 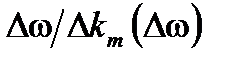 . Если эта скорость постоянна по всему спектру,
. Если эта скорость постоянна по всему спектру,  равны производным первого порядка
равны производным первого порядка  и производная второго порядка
и производная второго порядка  равна нулю. Член модуляции M (t,z) распространяет без каких-либо изменений с той же скоростью, как все его частотные компоненты, с так называемой групповой скоростью
равна нулю. Член модуляции M (t,z) распространяет без каких-либо изменений с той же скоростью, как все его частотные компоненты, с так называемой групповой скоростью 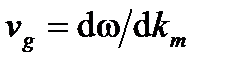 , поэтому он может быть записан
, поэтому он может быть записан
 (A1.55)
(A1.55)
Значение vg не зависит от ширины спектра, и этот результат является весьма общим. Он применяется для какой-либо функции M (т.е. амплитуда, фаза или частота модулируемых сигналов), но он также применяется, если спектр природного источника излучения широк.
|
|
|
Если  не постоянна по спектру (т.е.
не постоянна по спектру (т.е. 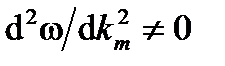 ), модуляционный член M (t,z) распространяется со средней групповой скоростью
), модуляционный член M (t,z) распространяется со средней групповой скоростью 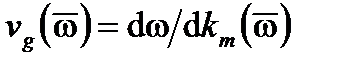 , и есть дополнительный эффект второго порядка временного распространения сигнала, который ограничивает пропускную способность передачи. Ограничения, вызванные этим эффектом внутри спектра, расширяющиеся за счет сигнала модуляции монохроматического источника, на практике незначительны, но они должны учитываться, когда спектр источников природных выбросов не является достаточно узким.
, и есть дополнительный эффект второго порядка временного распространения сигнала, который ограничивает пропускную способность передачи. Ограничения, вызванные этим эффектом внутри спектра, расширяющиеся за счет сигнала модуляции монохроматического источника, на практике незначительны, но они должны учитываться, когда спектр источников природных выбросов не является достаточно узким.
Давайте оценим для лучшего понимания порядки: средняя частота света 300,000 ГГц (на длине волны l мкм), спектральное расширение за счет модуляции сигнала электронным управлением составляет максимум несколько гигагерц (т.е. максимум около 10–5 центральной чаcтоты), а ширина спектра источника природного излучения может быть от 10–3 до 5×10–2 от центральной частоты (т.е., шириной от 1 до 50 нм в длинах волн). В этом случае модуляционный член M (t,z) сочетает комплексный эффект модулированного сигнала S (t,z) и случайных членов Mr (t,z), которые учитывают эффект влияния ширины спектра излучаемого источника. Можно рассмотреть, что каждая частота излучения ω e источника несет сигнал, который распространяется на этой частоте с групповой скоростью vg (ω e). На самом деле общий сигнал разлагается на элементарные сигналы, которые распространяются с различными скоростями, включающими в себя 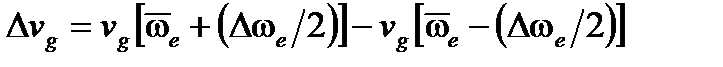 , где
, где  – средняя частота излучения спектра и
– средняя частота излучения спектра и 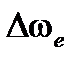 – ширина спектра излучения. Эти различия в скорости дают на распространяемой длине L, временные разбросы
– ширина спектра излучения. Эти различия в скорости дают на распространяемой длине L, временные разбросы 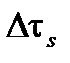 элементарных сигналов:
элементарных сигналов:
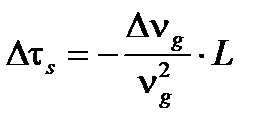 (A1.56)
(A1.56)
поскольку время группового распространения 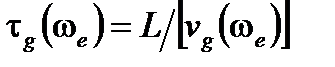 . Выразим правую часть через показатель преломления n и среднюю длину волны излучения
. Выразим правую часть через показатель преломления n и среднюю длину волны излучения 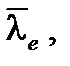
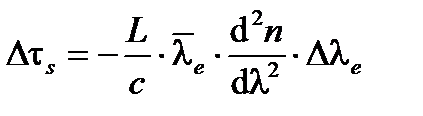 (A1.57)
(A1.57)
где 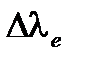 – ширина спектра излучения в длинах волн.
– ширина спектра излучения в длинах волн.
Например, для кремнезема, использующегося в оптических волокнах, с 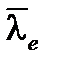 =850 нм и
=850 нм и 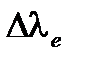 = 30 нм,
= 30 нм,
|
|
|

который ограничивает передаточную пропускную способность, менее, чем на 400 МГц на 1 км переноса.
С другой стороны, в кремнеземе 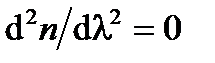 около 1300 нм, эта длина волны является оптимальным выбором для телекоммуникаций с большой пропускной способностью, которая требует минимального разброса сигнала. Обратите внимание, что когда
около 1300 нм, эта длина волны является оптимальным выбором для телекоммуникаций с большой пропускной способностью, которая требует минимального разброса сигнала. Обратите внимание, что когда 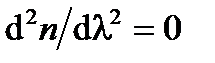 , часто говорят, что дисперсия не существует. Точнее надо сказать, что нет «распространения дисперсии.» Причиной этого является то, что даже с производными второго порядка
, часто говорят, что дисперсия не существует. Точнее надо сказать, что нет «распространения дисперсии.» Причиной этого является то, что даже с производными второго порядка 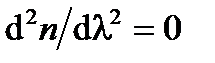 по-прежнему в призме можно получить хроматическую дисперсию, потому что она зависит от производной первого порядка d nl dλ.
по-прежнему в призме можно получить хроматическую дисперсию, потому что она зависит от производной первого порядка d nl dλ.
Примечание: основное электромагнитное поле – это набор электрического поля Е и магнитного поля В. Теория относительности показывает, что E и В соединены преобразованием Лоренца для движущейся опорной системы отсчета. Производные поля D и H являются только вспомогательными, которые позволяют обращаться с макроскопической средой. Это особенно видно в электромагнитной теории эффекта Саньяка, подробно изложенной в приложении 4.
Тем не менее, по историческим причинам многие книги по оптике и антеннам, которые посвящены главным образом неподвижной системе, рассматривают H как основное магнитное поле вместо В. Преимуществом (E, H) подхода является то, что он предлагает хорошие аналогии с другими волновыми явлениями. Фактически обычно в волне можно рассмотреть первый физический параметр – это "потенциал" и второй физический параметр – это "поток". Аргументом для объяснения, махнув рукой, распространения волн, является рассмотрение изменения "потенциала", которое вызывает изменение "потока". Затем этот вариант "поток" побуждает разновидность "потенциал" и так далее. Мощность P волны является продуктом "потенциала" при "потоке", и полное сопротивление (импеданс) Z распространению в среде представляет собой отношение "потенциала" над "потоком".
В электрических цепях "потенциал" это напряжение V и "поток" – это интенсивность электрического тока i, и мощность и импеданс
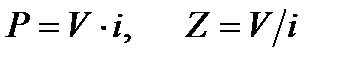 (A1.58)
(A1.58)
Для акустических волн, "потенциал" это колебания перепада давления Δ р, "поток" это фактически течение вещества f matter, и
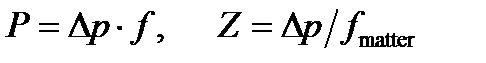 (A1.59)
(A1.59)
С электромагнитными волнами, поскольку размерность поля Е есть напряжение×длину–1 и размерность поля H ток×длину–1, импеданс Z определяется
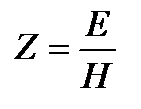 (A1.60)
(A1.60)
и имеет те же единицы, что и V / i (т.е. единицей является Ом (Ω)). В частности для волн в вакууме, есть так называемое сопротивление вакуума:
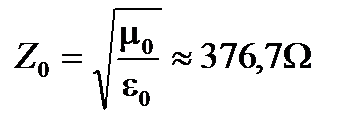 (A1.61)
(A1.61)
|
|
|
Можно доказать, что в среде с показателем преломления n получаем импеданс
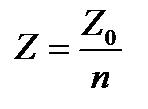 (A1.62)
(A1.62)
и частичное отражение на поверхности раздела может быть истолковано как несоответствие сопротивлению. Поле E будет «потенциал» и поле H будет "поток". Более того, продукт "потенциал" на "поток" имеет значение мощности, поскольку он соответствует так называемому вектору Пойнтинга П, который равен расходу мощности на единицу поверхности. В вакууме
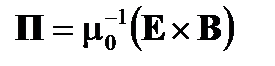 (A1.63)
(A1.63)
затем
 (A1.64)
(A1.64)
Как мы видим, это аналогия, использующая E как "потенциал"» и В в качестве "потока", имеет некоторый интерес, но общая тенденция в настоящее время в физике рассмотреть связь (Е, В) как основное электромагнитное поле. Тот факт, что соотношение E/B электромагнитных волн в вакууме равно скорости света является, в конце концов, более фундаментальным результатом, чем тот факт, что соотношение E/H имеет тех же единицы измерения, что и полное электрическое сопротивление.
Кроме того, обратите внимание, что мы использовали четыре физических константы электромагнетизма, которые не являются независимыми:
• ε0, диэлектрическая проницаемость вакуума;
• µ0, магнитная проницаемость вакуума;
• c, скорость света в вакууме;
• Z 0, импеданс вакуума.
Если преобладают релятивистские аргументы, то на самом деле есть только две основных физических константы:
• ε0, потому что без движения зарядов, есть только электрическое поле;
• c, потому что это основная константа относительности, которая объясняет трансформации путем движения.
Как мы уже видели, магнитные поле В выводится из поля электрического Е через релятивистское преобразование Лоренца, которое использует с. Тогда µ0 не должно быть основной константой: она должна быть выведена из µ0=1/ε0 c 2, даже если по историческим и практическим причинам µ0 является базовой константой в Международной системе единиц связанной с определением ампера. Подобным образом, Z 0, также вторичная физическая константа, вытекающая из Z 0=1/ε0 c. Теперь, вторичность не означает не полезность: исторически она имеет основополагающее значение для проверки, что измеренное значение скорости света с составляет 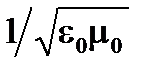 , ε0 и µ0 могут быть найдены самостоятельно в электростатических и магнетостатических экспериментах.
, ε0 и µ0 могут быть найдены самостоятельно в электростатических и магнетостатических экспериментах.
Как резерв, интересно отметить, что если с считается фундаментальной константой физики, используя (ct) как пространственную координату с размерностью длины и (c B) как магнитное поле с размерностью электрического поля, уравнения Максвелла в вакууме становятся очень симметричными и не подвергаются обвинениям в несимметрии. Они принимают вид:
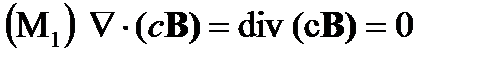 (A1.65)
(A1.65)
 (A1.66)
(A1.66)
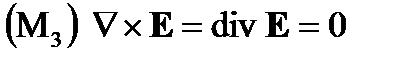 (A 1.67)
(A 1.67)
 (A1.68)
(A1.68)
|
|
|


