 |
Расчет метрологических параметров
|
|
|
|
Расчет метрологических параметров. На практике в количественном анализе обычно проводят не бесконечно большое число определений, а n=5-6 независимых определений, т. е. имеют выборку (выборочную совокупность) объемом 5-6 вариант. В оптимальном случае (при анализе, например, лекарственных препаратов) рекомендуется проводить 5 параллельных определений, т. е. оптимальный рекомендуемый объем выборки п = 5.
При наличии выборки рассчитывают следующие метрологические параметры в соответствии с распределением Стьюдента.
1) Среднее, т. е. среднее значение определяемой величины, согласно (1),
Среднее из конечной выборки отличается от действительного значения а (которое обычно не известно) и зависит от объема выборки п:
lim 
→ a
lim n → ∞
2) Отклонение d:
d1 = x1 - (4)
случайное отклонение i-й варианты от среднего.
3) Дисперсия V (иногда ее обозначают как s2) показывает рассеяние вариант относительно среднего и характеризует воспроизводимость анализа. Рассчитывается по формуле (5):
(5)
где f = n- 1 — так называемое число степеней свободы.
Если известно действительное значение определяемой величины (или истинное значение определяемой величины и), например при1 работ со стандартным образцом, то среднее принимают равным а (или ц тогда число степеней свободы f= п.
Дисперсия среднего V 
- равна
V = V/n
4) Стандартное отклонение (или среднее квадратичное отклонение) s -характеристика рассеяния вариант относительно среднего. Она рассчитывается как корень квадратный из дисперсии V, взятый со знаком плюс:
s = + 
(6)
Очевидно, V = s2. Стандартное отклонение s, как и дисперсия V, характеризует воспроизводимость количественного анализа.
Стандартное отклонение среднего s определяется как
|
|
|
s = s/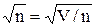 
(«старое» название — средняя квадратичная ошибка среднего арифметического).
Относительное стандартное отклонение s, — это отношение стандартного отклонения к среднему значению:
sr = s/ .
Чем меньше sr тем лучше воспроизводимость анализа.
5) Доверительный интервал (доверительный интервал среднего) — интервал, в котором с заданной доверительной вероятностью Р находите; действительное значение определяемой величины (генеральное среднее):
, (7)
где Δ — полуширина доверительного интервала.
Доверительная вероятность Р — вероятность нахождение действительного значения определяемой величины а в пределах доверительного интервала. Изменяется от 0 до 1 или (что то же самое) от 0%до 100%.В фармацевтическом анализе при контроле качества лекарственных пpeпapaтoв доверительную вероятность чаще всего принимают равной Р = 0,95 = 95% и обозначают как P0,95.При оценке правильности методик или методов анализа доверительную вероятность обычно считают равной
Р = 0,99 = 99%.
6) Полуширину доверительного интервала находят по формуле (8):
, (8)
где tP,f — коэффициент нормированных отклонений (коэффициент Стьюдета, функция Стьюдента, критерий Стьюдента), который зависит от
доверительной вероятности Р и числа степеней свободы f = n - 1 т е от
числа nпроведенных определений.
Численные значения tP,f рассчитаны для различных возможных величин Р и п и табулированы в справочниках.(Харитонов, стр 15).
В табл. приведены численные значения коэффициента Стьюдента, рассчитанные при разных величинах п и Р.
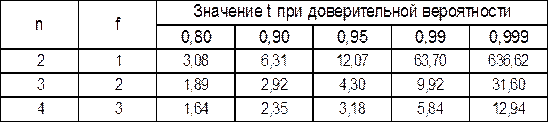
Чем больше п, тем меньше t. Однако при п > 5 уменьшение уже сравнительно невелико, поэтому на практике обычно считают достаточнымпроведение пяти параллельных определений(n=5).
7) Относительная (процентная) ошибка среднего результата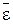 
:
(9)
|
|
|
