 |
Исключение грубых промахов
|
|
|
|
Исключение грубых промахов. Некоторые из результатов единичных определений (вариант), входящих в выборочную совокупность, могут заметно отличаться от величин остальных вариант и вызывать сомнения в их достоверности. Для того чтобы статистическая обработка результатов количественного анализа была достоверной, выборка должна быть однородной, т. е. она не должна быть отягощена сомнительными вариантами — так называемыми грубыми промахами. Эти грубые промахи необходимо исключить из общего объема выборки, после чего можно проводить окончательное вычисление статистических характеристик.
Если объем выборки невелик 5 ≤ п < 10, то выявление сомнительных результатов анализа — исключение грубых промахов — чаще всего проводят с помощью так называемого Q-критерия (контрольного критерия Q), или Q-теста. Для этого варианты хi располагают в порядке возрастания их численного значения от xi до хn, где п — объем выборки, т. е. представляют в виде упорядоченной выборки. Затем для крайних вариант — минимальной хi и максимальной хn — вычисляют величину Q по формулам (10):
Q1=(x2-x1)/R;Qn=(xn –xn-1)/R, (10)
где х2 и xn-1 — значения вариант, ближайших по величине к крайним вариантам, а
R = xn – x1
— размах варьирования, т.е. разность между максимальным хn и минимальным x1 значениями вариант (между крайними вариантами), составляющих выборку.
Рассчитанные значения Q1 и Qn сравнивают с табличными при заданных п и доверительной вероятности Р. Если рассчитанные значения Q1 или Qn (или оба) оказываются больше табличных
Q1 >Qтабл. или Qn > Qтабл,
то варианты х1 и хn (или обе) считаются грубыми промахами и исключаются из выборки.
В таблице приведены численные величины контрольного критерия Q для Р = 0,90-0,99 и n = 3-10
|
|
|
Для полученной выборки меньшего объема проводят аналогичные расчеты до тех пор, пока не будут исключены все грубые промахи, так что окончательная выборка окажется однородной и не будет отягощена грубыми промахами.
При проведении Q-теста доверительную вероятность чаще всего принимают равной Р = 0,90 = 90%.
Если из двух крайних вариант х1 и хn только одна вызывает сомнение, то Q-тест можно проводить лишь в отношении этой сомнительной варианты.
Если объем выборки равен 3 или 4, т. е. п < 5, то применение Q-теста не рекомендуется.
Представление результатов анализа.
Представление результатов количественного анализа. При представлении результатов количественного анализа обычно указывают и рассчитывают следующие статистические характеристики: хi — результаты единичных определений (варианты); п — число независимых параллельных определений (объем выборки); 
— среднее значение определяемой величины; s — стандартное отклонение; Δ — полуширину доверительного интервала (с указанием значения доверительной вероятности Р), ± Δ — доверительный интервал (доверительный интервал среднего);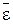 
— относительную (процентную) ошибку среднего результата.
Эти характеристики составляют необходимый и достаточный минимум величин, описывающих результаты количественного анализа, при условии, что систематические ошибки устранены или они меньше случайных.
ЭТАЛОНЫ РЕШЕНИЯ ЗАДАЧ
Задача 1
Пусть содержание определяемого компонента в анализируемом образце, найденное в пяти параллельных единичных определениях (n = 5), оказалось равным, %: 3,01; 3,04; 3,08; 3,16 и 3,31. Известно, что систематическая ошибка отсутствует. Требуется провести статистическую обработку результатов количественного анализа (оценить их воспроизводимость) при доверительной вероятности, равной Р - 0,95.
|
|
|
Решение:
1) Проведем оценку грубых промахов с использованием Q- критерия. Сомнительным значением может быть величина 3,31. Согласно формулам (1.10), имеем:
Q рассч= (3,31 – 3,16)/(3,31 – 3,01) = 0,50.
Табличное значение Qтабл при n = 5 и Р = 0,90 равно (табл. 1.2) Qтабл = 0,64. Поскольку Q рассч = 0,50 < Qтабл = 0,64, то значение варианты 3,31 не является грубым промахом. Выборка однородна.
2) Рассчитаем среднее значение , отклонения d1 и сумму квадратов отклонений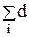 
12:
= (3,01 + 3,04 + 3,08 + 3,16 +3,31)/5 = 3,12;
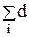12 = 0,0121+ 0,0064 + 0,0016 + 0,0361 = 0,0578.
Таблица отклонений
| х1 | d1 = x1 -
| d12 |
| 3,01 3,04 3,08 3,16 3,31 | 3,01 – 3,12 = - 0,11 3,04 – 3,12 = - 0,08 3,08 – 3,12 = -0,04 3,16 – 3,12 = 0,04 30,31 – 3,12 = 0,19 | 0,0121 0,0064 0,0016 0,0016 0,0361 |
3) Определяем стандартное отклонение по формуле (6):
s= [ 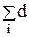12 /(n-1)]0.5 = (0,0578/4)0.5 = 0,12
4) Определяем полуширину доверительного интервала среднего Δ формуле (8) при п = 5 и Р = 0,95:
Δ = tP,f s/ 
.
Коэффициент Стьюдента заимствуем из таблицы 1:
tP,f s = t 0,95;4 = 2,78.
Тогда Δ = 2,78 · 0,12/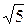 
= 0,15.
Доверительный интервал среднего: + Δ = 3,12 + 0,15.
5)Рассчитываем относительную ошибку среднего 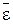по формуле (9):
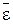= (Δ / )· 100% = (0,15/3,012) · 100% = 4,8%.
6)Составляем итоговую таблицу, представляющую результаты анализа.
Итоговая таблица
| xi | 3,01; 3,04; 3,08; 3,16; 3,31 |
| n | |
|
| 3,12 |
| s | 0,12 |
| Δ
| 0,15 (P = 0,95) |
| + Δ
| 3,12 ± 0,15 |
|
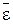
| 4,8 % |
На этапе составления итоговой таблицы завершается представление результатов статистической обработки данных количественного анализа.
|
|
|
