Описание лабораторной установки

Законы вращательного движения проверяются на установке, называемой маятником Обербека, который представляет собой крестовину, вращающуюся вокруг горизонтальной оси (Рис. 2). На шкив радиуса r наматывается нить, к которой через блок прикреплен подвес. Подвес представляет собой плоские цилиндры с прорезью для их закрепления на нить. Подвес при опускании движется вдоль вертикальной линейки, на которой отмечаются начальная и конечная точки движения. С помощью секундомера фиксируется точное время движения между этими точками.

подвес

Рис. 2

 

ПОДГОТОВКА К ВЫПОЛНЕНИЮ РАБОТЫ

Перед выполнением лабораторной работы необходимо установить основные физические закономерности, наблюдаемые на маятнике Обербека. Второй закон Ньютона, применимый к описанию движения подвеса запишется как:

Сила, приложенная к оси крестовины радиуса r маятника Обербека:

а момент силы:

(3)

Момент инерции маятника Обербека определится из уравнения 1 как:

Для проверки закона вращательного движения необходимо определить моменты инерции грузов на крестовинах маятника Обербека, закрепленных на различных расстояниях R от оси вращения. Согласно определению момен­та инерции вращающихся тел J является функцией R², т.е. для одного и того же тела массы m:

Для любых расстояний от оси вращения можно записать:

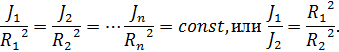
Линейное ускорение a в формуле (3) можно связать с угловым ускорением, используя законы кинематики:

(5)

Тогда момент инерции маятника:

(6)

Если подвес подает из неподвижного положения с высоты h, то ускорение a определится из закона равноускоренного движения:

(7)

где t – время опускания груза.

Таким образом, при обработке результатов эксперимента нам понадобятся формулы (3), (6) и (7). Отметим, что в данном рассмотрении мы пренебрегаем силами трения в осях вращающихся деталей. Исходя из малых числовых значений линейного ускорения а, следует ускорение свободного падения брать с точностью до сотых единиц: g = 9.81 .

ЗАДАНИЕ

 

I часть работы:

Определение собственного момента инерции крестовины.

1. Для числовых обработок определите заранее массу подвеса , с помощью штангенциркуля измерьте радиус шкива намотки нити r, измерьте высоту опускания подвеса h.

2. Намотайте нить на шкив и из зафиксированного положения опустите подвес с одновременным включением секундомера.

3. Измерьте три раза время падения каждой из выбранных масс подвесов. Время движения удобно считать до удара подвеса о пол.

4. Данные измерений и расчетов ускорений движения, моментов сил и моментов инерции по формулам (7, 6, 3) занесите в таблицу 1.

 

Таблица 1

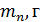
	t, с		Н·м	, кг·	, кг·

 

 

II часть работы.

Установление зависимости момента инерции тела от квадра­та расстояния до оси вращения.

1. Выберите и зафиксируйте подвес с винтами.

2. На крестовине маятника Обербека закрепите симметрично два груза.

3. Намотайте нить на шкив и трижды определите время опускания подвеса для двух-трех различных положений грузов на крестовине маятника.

4. Данные измерений времени опускания, расстояния грузов от оси вращения, расчетов ускорений движения, моментов сил и моментов инерции по формулам (7, 6, 3) занесите в таблицу 2.

5. Полагая, что момент инерции маятника с грузами равен сумме собственного момента инерции маятника и моментов грузов, найдите моменты инерции двух грузов. Для этого воспользуйтесь данными таблицы 1.

6. Оцените соотношение .

Таблица 2

	t, с		Н·м	, кг·	, кг·

III часть работы.

 

Рассчитайте погрешность определения моментов инерции грузов на осях маятника.

 

1. Выведите формулу для определения погрешности а.

2. Выведите формулу и определите погрешность измерения момента инерции.

3. Сделайте вывод о результатах работы и точности измерений.

 

ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА

1. Савельев И. В. «Курс общей физики», т.1, гл. V, § 35, 36, 38, 39.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Вывести формулу основного закона динамики вращательного движения.

2. Провести аналогию между параметрами кинематики и динамики поступательного и вращательного движения. Указать единицы измерения ос­новных величин.

3. Какое движение называется вращательным? Приведите примеры. В каких случаях размером тел при рассмотрении законов движения можно пре­небречь.

4. Дайте определение момента инерции твердого тела. Расскажите о теореме Штейнера.

5. Как в данной работе определить момент инерции маятника Обербека без грузов?

6. Как в данной работе определить массу грузов на стержнях маятника Обербека?

7. Как можно изменить момент инерции маятника Обербека?

8. Если увеличить высоту опускания подвеса, то какие величины изменяются и как: (момент инерции маятника, время опускания подвеса, кинетическая энергия системы маятник-груз, угловое ускорение маятника)?

 

ЗАДАЧИ

1. Найти линейную скорость Земли при ее движении по орбите. Средний радиус земной орбиты R = 1,5· км.

 

2. Автомобиль движется со скоростью 60 . Сколько оборотов в секунду делают его колеса, если они катятся без скольжения, а внешний диаметр покрышек колес равен 60 см? Найти величину центростремительного ускорения точек на покрышках колес.

 

3. Человек находится на краю круглой горизонтальной платформы радиусом 4 м. Сколько оборотов в минуту должна делать платформа вокруг вертикальной оси, чтобы человек мог удержаться на ней при коэффициенте трения μ = 0,27?

 

4. Совершает ли работу равнодействующая всех сил, приложенных к телу, равномерно движущемуся по окружности?

 

5. Мотоциклист едет по горизонтальной дороге со скоростью 74 , делая поворот радиусом кривизны 100 м. На сколько при этом он должен наклониться, чтобы не упасть на повороте?

 

6. Самолет делает «мертвую петлю» с радиусом R = 100 м и движется по ней со скоростью 280 . С какой силой тело летчика, массой 80 кг будет давить на сидение самолета в верхней и нижней точках петли?

 

7. Определить момент инерции диска относительно оси, проходящей через точку на краю диска перпендикулярно его плоскости.

 

8. Сплошной диск массой 20 кг и радиусом 120 мм вращается с угловой скоростью 600 . С какой силой нужно прижать к нему горизонтальную колодку, чтобы диск остановился через 3 с, если коэффициент трения μ = 0,1?

 

9. Диск совершает 70 . Где можно положить на диск тело, чтобы оно не соскользнуло? Коэффициент трения покоя μ = 0,44.

 

10. Точка движется по окружности радиусом R = 10 см с постоянным тангенциальным ускорением: . Найти тангенциальное ускорение точки, если известно, что к концу пятого оборота после начала движения скорость точки стала V = 79, 2 .

 

Работа 3.1

«ИЗУЧЕНИЕ ЭЛЕКТРОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ»

ЦЕЛЬ РАБОТЫ

 

1. Изучить основные электроизмерительные приборы, освоить методику измерения с помощью этих приборов.

2. Используя амперметр и вольтметр определить величину неизвестного сопротивления.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: