Основные теоретические сведения

Термоэлектронной эмиссией называется испускание электронов нагретыми телами. Это явление широко применяется на практике, на нем основана работа радиоламп, электронно-лучевых трубок в телевизорах и осциллографах.

Рассмотрим испускание электронов нагретыми металлами. С совре­менной точки зрения металл представляет собой расположенные в строгом порядке положительные ионы металла, образующие кристаллическую структуру. Элементарной ячейкой кристаллической решетки называется наименьшая упорядоченная совокупность атомов, сохраняющая свойства вещества в целом. Например, элементарной объемно-центрированной ячейкой железа является куб, в вершинах которого расположены ионы железа и еще один ион — в центре куба. Из таких элементарных ячеек и состоит кристалл железа.

В кристаллической структуре находятся свободные электроны или электроны проводимости. Они принадлежат не конкретным атомам, а всему кристаллу в целом и могут свободно перемещаться по кристаллу. Наличием свободных электронов и обусловлена высокая электро- и теплопроводность металлов.

В рамках квантовой механики электроны проводимости можно рас­сматривать как свободные. Однако при этом они характеризуются эффектив­ной массой — величиной, учитывающей взаимодействие свободных электро­нов с потенциальными энергетическими полями кристаллической структуры. Эффективная масса может существенно отличаться от массы покоя электрона и является индивидуальной характеристикой кристалла.

В модели свободных электронов кристаллическая структура из положительных ионов создает электрическое поле с положительным потенциалом . Следовательно, потенциальная энергия свободного электрона в таком поле может быть рассчитана:

Считая, что при удалении электрона из металла потенциальная энергия их взаимодействия стремится к нулю, график потенциальной энергии свободных электронов можно представить так, как на Рис. 1.

Рис. 1. Распределение свободных электронов по энергиям в одномерном энергетическом поле кристалла металла

 

Форма потенциальной энергии напоминает «потенциальную яму» для электронов. По ординате отложена энергия электронов, по абсциссе — рас­стояние, ширина «ямы» соответствует линейному размеру кристалла.

В соответствии с квантовой механикой энергия электрона в кристалле может принимать лишь строго определенные значения. Разрешенные значе­ния энергии образуют систему дискретных уровней — зону. Отметим, что разность энергий соседних уровней очень мала (ΔW~10^-22эВ).

Согласно принципу запрета Паули, на каждом энергетическом уровне может находиться один электрон. Поэтому суммарная электронная энергия соответствует тому, что энергетические уровни заполнены электронами снизу вверх до наибольшего значения W_F.W_F — энергия уровня Ферми - максимальная энергия свободного электрона в металле при температуре абсолютного нуля.

Из Рис. 1 видно, что энергия внутри меньше, чем энергия вне металла. Наименьшее значение энергии свободного электрона, удаленного из вещества, можно принять условно за нулевой энергетический уровень. Следовательно, для того, чтобы удалить электрон из металла надо затратить энергию А, называемую работой выхода. Работа выхода — минимальная энергия необходимая для вырывания электрона с поверхности вещества. Для металлов она соответствует нескольким электрон-вольтам: в системе СИ 1 эВ = 1,6·10 ^-19 Дж.

При комнатной температуре энергия большинства электронов не превышает W_F. Она меньше величины потенциального барьера, равного разнице энергий вне металла и внутри него, и электроны не могут покинуть металл.

Однако, если электрону передать дополнительную кинетическую энергию, превышающую А, путем нагрева тела, возникает явление термоэлектронной эмиссии.

Явление термоэлектронной эмиссии можно изучить на примере работы радиолампы-диода. Простейший диод представляет собой вакуумированный стеклянный баллон с впаянными электродами. Катодом может служить спираль накала, расположенная по оси цилиндра-анода. Типичная схема включения диода приведена на Рис. 2.

Рис. 2

 

При прохождении тока нить накала разогревается и за счет термоэлек­тронной эмиссии вокруг нее возникает электронное облако. Но эмитирован­ные электроны не могут удалиться, поскольку на них действует кулоновская сила притяжения со стороны, оказывающейся положительно заряженной ни­ти. Устанавливается динамическое равновесие между эмитированными и вернувшимися электронами. Однако наиболее «энергичные» обладающие наибольшим значением скорости, а значит и кинетической энергии, могут преодолеть поле притяжения катода и долететь до анода. Таким образом, даже при отсутствии напряжения между анодом и катодом возникает слабый анодный ток (Рис. 3).

 

Обратимся к анализу ВАХ. Для прекращения слабого анодного тока в отсутствие электрического поля (Ua=0), на анод нужно подать отрицательное запирающее напряжение U₃ (Рис. 3). При подаче на анод положительного, по отношению к катоду, потенциала возникает электрическое поле. В этом поле эмитированные электроны начинают двигаться от катода к аноду, анодный ток усиливается. Сила анодного тока зависит от материала катода, его температуры и величины электрического поля. Зависимость анодного тока от приложенного анодного напряжения при фиксированной температуре катода называется вольтамперной характеристикой (ВАХ). Типичные ВАХ при различных температурах катода приведены на Рис. 3.

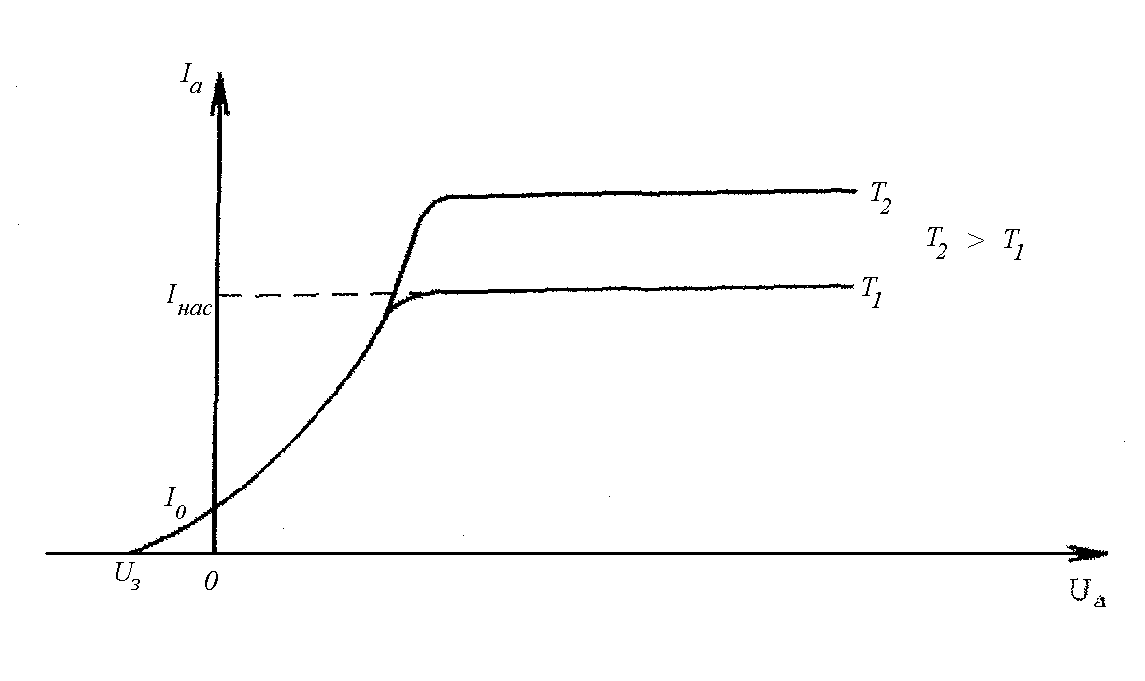
Рис. 3

При неизменной температуре катода с увеличением анодного напряжения анодный ток увеличивается за счет все большего количества электронов, оттягиваемых электрическим полем от катода. Отметим, что ВАХ нелинейна, т. е. не подчиняется закону Ома, что обусловлено неравномерным пространственным зарядом между электродами.

В рабочем режиме лампы, далеком от насыщения, ВАХ подчиняется закону Богуславского-Лэнгмюра или закону «трех вторых»:

где С — константа, зависящая от формы и расположения электродов.

С дальнейшим увеличением U_a все эмитированные электроны долетают до анода и анодный ток перестает изменяться, говорят происходит «насыщение одной характеристики при изменении другой». Ток насыщения зависит от количества электронов, испускаемых катодом в единицу времени, которое определяется температурой катода. Эта зависимость описывается формулой Ричардсона-Дэшмана:

(1)

Здесь В — постоянная, зависящая от типа катода и его площади, Т — абсолютная температура катода, ехр — экспонента, показательная функция числа е, где е — основание натуральных логарифмов, k — постоянная Больцмана. С помощью формулы (1), зная температуру катода и анализируя ВАХ, можно определить работу выхода электрона.

Для определения температуры катода нити накала воспользуемся зави­симостью сопротивления металла от температуры.

(2)

где а — температурный коэффициент сопротивления металла, t — темпера­тура в градусах Цельсия, R — сопротивление нити накала при температуре t, R₀ — сопротивление при нуле градусов Цельсия.

 

 

Из формулы (2) можно получить абсолютную температуру катода в шкале Кельвина, Т = t + 273:

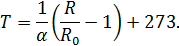
Сопротивление нити накала можно измерить, например, с помощью амперметра и вольтметра, включенных в цепь накала катода.

Предположим, что мы измерили ток насыщения 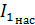при температуре катода Т₁ и ток насыщения при температуре Т₂. В соответствии с формулой (1) запишем отношение этих токов насыщения:

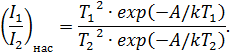
Логарифмируя это выражение, легко получить формулу для расчета работы выхода:

(3)

Отметим, что в наших экспериментах температуры Т₁ и Т₂ — близки, поэтому в формуле (3) в первом приближении можно пренебречь в числителе вторым слагаемым. Для того, чтобы получить величину А в электрон-вольтах, формулу (3) нужно разделить на заряд электрона. С учетом этих замечаний выражение для работы выхода принимает вид:

(4)

Обратим внимание, что токи насыщения можно измерять в любых одинаковых единицах, т.к. в формуле (4) стоит логарифм отношения токов.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: