 |
Основные теоретические сведения
|
|
|
|
Любое заряженное тело создает в пространстве вокруг себя электрическое поле и может взаимодействовать с внешним электромагнитным полем. Поле, создаваемое неподвижными зарядами, называется электростатическим. Знание характеристик электрического поля требуется при работе с линиями связи, антеннами, резонаторами, полупроводниковыми приборами и другими устройствами.
Величину взаимодействия между зарядами определяет Закон Кулона, являющийся основополагающим для всей науки об электричестве, который был установлен еще в 1780 г.:
| (1) |
Здесь 
и 
- величины взаимодействующих зарядов, r – расстояние между ними, 
- диэлектрическая проницаемость, характеризующая среду между зарядами, 
, электрическая постоянная, 
- единичный вектор, задающий направление силы от первого заряда ко второму.
Электростатическое поле в каждой точке пространства характеризуется двумя величинами: напряженностью и потенциалом. Силовая характеристика поля — напряженность — векторная величина, численно равна и совпадает с силой, действующей на единичный точечный положительный заряд, помещенный в данную точку поля:
| (2) |
Из определения напряженности следует, что сила, действующая со стороны электрического поля на точечный заряд, равна:
|
Единица измерения напряженности электрического поля – 
.
Исходя из закона Кулона и определения (1), легко рассчитать напряженность электрического поля точечного заряда в вакууме:
| (3) |
Электрическое поле характеризуется также потенциалом — энергетической величиной, численно равной работе по переносу единичного, положительного, точечного заряда q из данной точки поля r в бесконечность:
|
|
|
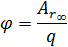
| (4) |
Потенциал измеряется в вольтах: 
Потенциал точечного заряда в вакууме равен:
| (5) |
Отметим, что потенциал — скалярная величина, которая может принимать и отрицательные значения. Физический смысл имеет величина, называемая разность потенциалов. Разность потенциалов связана с работой сил электрического поля по перемещению точечного заряда из точки с потенциалом 
в точку с потенциалом 
следующим образом:
| (6) |
Наконец, напомним, что введение понятий потенциала и разности потенциалов электрического поля связано с тем, что работа по перемещению заряда в электрическом поле не зависит от траектории перемещения, а определяется лишь начальным и конечным положением заряда.
Напряженность и потенциал — две характеристики электростатического поля. Для нахождения связи между ними рассчитаем работу при малом перемещении точечного заряда q в электрическом поле из точки О в точку А (Рис. 1)
Рис. 1.
Элементарная работа при таком перемещении вычисляется так:
| (7) |
В соответствии с формулой (6) эта же работа равна:
 .
| (8) |
Сопоставляя формулы (7) и (8) и учитывая выражение для силы (2), получим напряженности в трехмерном пространстве:
 .
| (9) |
Здесь 
Тогда для случая одномерного пространства при перемещении заряда вдоль оси х на расстояние dx при фиксированных значениях координат y и z (
). В соответствии с формулой (9) получим:
|
Последнюю формулу перепишем так:
| (10) |
где частная производная находится путем дифференцирования потенциала по координате х при фиксированных значениях у и z.
По аналогии можно получить выражение для проекции вектора напряженности на другие оси координат:
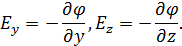
| (11) |
Из полученных проекций легко «сконструировать» вектор напряженности электрического поля:
|
Выражение в скобках называется градиентом потенциала и сокращенно записывается так:
 или  .
| (12) |
Градиент функции — это вектор, характеризующий скорость пространственного изменения функции и направленный в сторону максимального возрастания этой функции. Как видно из формулы (12), вектор напряженности электрического поля направлен в сторону, противоположную максимальному возрастанию потенциала.
|
|
|
Отметим, что во многих практических задачах требуется определить значение напряженности электрического поля. Формула (12) упрощается, если электрическое поле однородно, обладает центральной симметрией:
| (13) |
Электростатическое поле удобно изображать графически с помощью силовых линий и эквипотенциальных поверхностей. Принято силовые линии электрического поля в пространстве проводить таким образом (Рис. 2), чтобы
касательная к ним совпадала с направлением вектора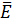 
в данной точке.
Эквипотенциальные поверхности — поверхности, во всех точках которой потенциал имеет одно и то же значение. Эти поверхности целесообразно проводить так, чтобы разность потенциалов между соседними поверхностями была одинаковой. Тогда по густоте эквипотенциальных поверхностей можно наглядно судить о значении напряженности поля в разных точках. Величина напряженности больше там, где гуще эквипотенциальные поверхности. В качестве примера на Рис. 2 приведено двумерное отображение электростатического поля.
Рис. 2 Рис. 3
Покажем, что в каждой точке вектор 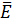перпендикулярен эквипотенциальной поверхности и направлен в сторону уменьшения потенциала. Для этого рассчитаем работу по перемещению заряда q вдоль эквипотенциальной поверхности на расстояние dr, (Рис. 3). Такая работа равна нулю, поскольку определяется разностью потенциалов точек 1 и 2..
.
С другой стороны работа записывается так:
| (14) |
Из формулы (14) следует, что косинус угла между векторам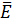и и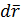 
равен нулю и вектор 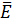перпендикулярен эквипотенциальной поверхности. За направление вектора 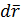принято считать направление скорости перемещения положительного точечного заряда вдоль эквипотенциальной поверхности.
Далее, переместим положительный заряд по нормали 
к эквипотенциальной поверхности в сторону уменьшения потенциала. В этом случае 
и из формулы (13) следует, что Еr > 0. Значит вектор 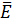направлен по нормали в сторону уменьшения потенциала.
|
|
|
|
|
|
