 |
Интегрирование рациональных дробей
|
|
|
|
Рассмотрим более подробно методы для интегралов типа 
, где 
- два многочлена каких-либо степеней.
Если степень числителя больше или равна степени знаменателя, то дробь неправильная. Можно свести неправильную дробь к правильной, поделив 
на 
с остатком. В результате, появятся некоторые степенные слагаемые вне этой дроби, найти первообразные от них не проблема. Таким образом, мы должны научиться интегрировать именно правильные дроби.
Есть некоторые виды дробей, действия с которыми сводятся к тем методам, которые мы уже изучали, это так называемые «простейшие дроби» (у них знаменатель дальше нельзя разложить на множители).
= 
заменой сводится к 
, а далее как для степенной.
= 
.
(обозначим этот интеграл 
) решается интегрированием по частям, если обозначить всю функцию u а второй множитель 1. Получится «рекурсивная» формула, выражающая 
к , значит, все они сводятся к 
.
решается так: выделить полный квадрат, и тогда всё сведётся к виду 
.
выделить полный квадрат в знаменателе, и получится выражение вида 
.
Рассмотрим общий случай, когда степень знаменателя произвольна. Дробь при этом уже правильная, если не так, то мы отделили целую часть и проинтегрировали её отдельно.
Найдём корни знаменателя и разложим его на множители. При этом неразложимые множители могут остаться либо 1 либо 2 степени. Для любого многочлена 3 степени, уже есть хотя бы один действительный корень. Итак, в знаменателе могут быть только 
или 
.
Далее, можно разбить на сумму простейших дробей, где знаменатель каждой дроби - это один из множителей, на которые был разложен знаменатель . Например, если все корни различны, то
Называется метод неопределённых коэффициентов.
|
|
|
Если сумму простейших привести к общему знаменателю, то останется приравнять числители, и найти неопределённые коэффициенты.
Ситуация 1) Если все корни 
и различны.
Пример. 
.
Решение.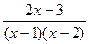 
= 
.
Приведём к общему знаменателю = 
.
Теперь приравняем числители в и .
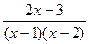, т.е.
, получается система уравнений:
решая её, находим 
.
Получается, что = 
=
= 
.
Ситуация 2. Если все корни , но среди них есть кратные.
Например, если два из 3 корней совпадают, дробь имеет такой вид: 
. Здесь нельзя записать 
и представить в виде 
, потому что, приводя к общему знаменателю такую сумму, мы получим в знаменателе только 
, а вовсе не 
. Таким образом, тот вариант метода разложения на простейшие, который был для различных корней, здесь приведёт к противоречию.
Разложение необходимо искать в таком виде:
Если корень кратности 
, то соответственно, надо включить в общую сумму таких слагаемых, где есть все степени от 1 до .
Пример. Вычислить интеграл 
.
Решение. Наличие множителя 
означает, что корень 0 кратности 2. Фактически даже можем рассматривать в таком виде: 
.
Сначала извлечём дробь из интеграла, и ищем разложение в виде:
= 
Приводим к общему знаменателю.
= 
Так как знаменатели равны, то осталось приравнять числители.
= 
,
=
=
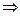
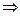
Тогда надо приравнять коэффициенты при каждой степени, получится 
, 
, 
.
То есть система уравнений на поиск трёх неопределённых коэффициентов:
решая эту систему, находим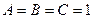 
.
Тогда исходный интеграл распадается на сумму:
= 
= 
= 
.
ЛЕКЦИЯ № 2. 21. 02. 2017
Продолжение - рациональные дроби.
Ситуация 3. Если не все корни .
Возможно, что многочлен в знаменателе дроби не полностью разлагается на первые степени, так, могут присутствовать множители 2 степени типа 
или 
с отрицательным дискриминантом, которые далее нельзя разложить, потому что у них нет действительных корней (есть комплексные корни, но они 
). В этом случае вместо пары слагаемых в разложение надо включать одно, вида 
, т.е. правильная дробь с максимально возможной степенью в числителе, должна содержать там линейную функцию. В некоторых примерах может потом оказаться, что 
, однако сразу искать в виде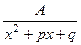 
нельзя, иначе может получаться противоречие при приведении к общему знаменателю.
|
|
|
А если неразложимые множители 2 степени сами кратные, то надо включить в сумму несколько слагаемых, где степени идут по нарастающей:
+ 
+...
Пример. Вычислить интеграл 
.
Решение. Ищем разложение в виде: 
= 
.
Приводим к общему знаменателю.
= 
= 
=
= .
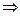
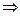
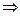
Получаем систему:
. Из разности 1-го и 2-го уравнения, получаем 
.
В то же время, 
. Тогда 
. Тогда .
Итак, заменим в интеграле «большую» дробь на сумму маленьких, каждая из которых приводится к табличному интегралу.
= 
= 
.
Итак, в этом параграфе мы рассмотрели все типы рациональных дробей. Других случаев нет, т.к. неделимых множителей 3 степени уже быть не может, для многочлена 3 степени есть хотя бы один действительный корень.
|
|
|
