 |
пункт 3. Линейные уравнения.
|
|
|
|
Уравнение вида 
называется линейным.
Если 
, то оно называется линейным однородным.
При этом, 
не может быть тождественно равно 0, иначе вообще нет слагаемого с производной 
, то есть уравнение не являлось бы дифференциальным. Но тогда можно поделить всё уравнение на и свести к виду 
.
Линейные однородные уравнения фактически являются уравнениями с разделяющимися переменными. Действительно, 
,
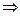
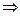
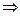
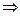
где 
первообразная, с точностью до константы. В итоге, 
, то есть общее решение линейного однородного уравнения имеет вид: константа, умноженная на экспоненту в степени первообразной от коэффициента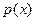 
, взятую с другим знаком.
Пример. Решить уравнение 
.
.
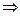
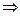
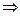
Мы видим коэффициент 
, её первообразная 
, соответственно в ответе есть 
.
Пример. Решить уравнение 
.
Можно рассмотреть 
, первообразная равна 
,
тогда = 
.
Впрочем, можно его решить и просто как уравнение с разделяющимися переменными:
.
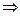
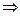
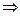
Линейные неоднородные уравнения. Метод Лагранжа (другое название: метод вариации произвольной постоянной).
Предположим, что на месте C некоторая неизвестная функция, и ищем решение в виде: 
.
Тогда 
.
Подставим эти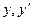 
в неоднородное уравнение .
+ 
.
Два слагаемых получились одинаковые, и они сокращаются, осталось:
= 
.
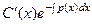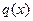Отсюда можно выразить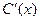 
. 
.
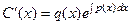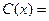
что состоит в итоге из 2 слагаемых:
первообразной от 
и константы 
. Поэтому решение однородного обязательно окажется отдельным слагаемым в общем решении неоднородного.
.
В конкретных примерах, это выглядит менее громоздко:
Пример. Решить линейное уравнение 
.
1 шаг. Решаем соответствующее однородное уравнение. . 
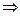
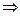
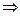
- общее решение однородного.
2 шаг. Методом Лагранжа решаем неоднородное.
|
|
|
Ищем решение в виде: 
. Ищем производную:
= 
. Всё это подставим в неоднородное:
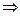
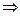
, тогда 
.
Тогда 
= 
.
Теперь подставим это в , получается
= 
.
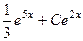Общее решение неоднородного состоит из двух слагаемых: частное решение неоднородного (его мы и искали на 2-м шаге методом Лагранжа) и общее решение однородного, которое нашли на 1-м шаге, и оно воспроизвелось само в конце 2-го шага. Это происходит из-за того, что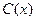 
всегда ищется с помощью её производной, а значит, в ней присутствует слагаемое 
.
Проверка. Можно подставить частное решение неоднородного, и это слагаемое само по себе тоже является решением:
Выполняется ли ?
= 
= 
. Верно.
Пункт 4. Уравнения Бернулли.
Уравнение вида 
называется уравнением Бернулли. Так как коэффициент не тождественно равен 0, то на него можно поделить, поэтому будем рассматривать в виде: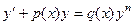 
.
Отличаются от линейных только наличием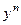 
в правой части.
Если n=0 получается линейное неоднородное .
Если n=1 то ещё лучше, получается однородное: 
то есть 
.
При 
, 
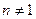получается уже собственно, уравнение Бернулли. Оно является обобщением линейного уравнения.
Алгоритм решения.
1) Разделить на 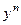. Получится 
.
2) Сделать замену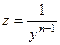 
. Тогда оно сведётся к линейному по 
.
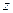3) решить линейное (в 2 шага, сначала однородное, потом неоднородное)
4) сделать обратную замену: так как 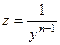, то 
.
Докажем подробнее, как и почему сводится к линейному.
, тогда 
по правилам дифференцирования композиции. Получили, что 
.
Тогда уравнение сводится к такому виду:
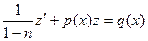, или 
.
Это уже линейное неоднородное уравнение.
Приложение 1. Вопросы на доказательства (для билетов).
Лекция № 1
1. Докажите формулу интегрирования по частям.
Лекция № 2
1. Доказать, что замена 
, где r = НОК (r1,...,rk) сводит интеграл 
к интегралу от рациональной дроби.
2. Доказать, что замена замена 
сводит интеграл вида 
к интегралу от рациональной дроби.
3. Вывести формулы преобразования синуса и косинуса
|
|
|
для универсальной тригонометрической замены 
.
4. Доказать, что в случае, когда функция нечётна относительно косинуса, замена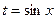 
сводит интеграл к рациональной дроби.
5. Доказать, что в случае, когда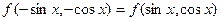 
замена: 
сводит интеграл к рациональной дроби.
6. Доказать, что для интеграла вида 
замена 
своит интеграл к рациональной дроби.
7. Доказать формулу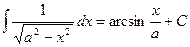 
8. Доказать, что для интеграла вида 
замена 
своит интеграл к рациональной дроби.
9. Доказать, что для интеграла вида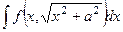 
замена 
сводит интеграл к рациональной дроби.
Лекция № 3
1. Доказать, что функция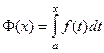 
является первообразной от функции 
.
2. Доказать формулу Ньютона- Лейбница: 
.
3. Доказать формулу длины явно заданной кривой:
.
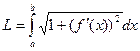4. Доказать формулу длины кривой, заданной в полярных координатах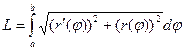 
Лекция № 4
Докажите теорему: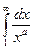 
сходится 
, 
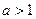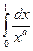сходится 
.
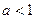Лекция № 5
1. Вывести (доказать) формулу площади явно заданной поверхности 
.
2. Вывод формул перехода к полярным координатам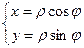 
.
3. Вывод определителя Якоби полярных координат 
.
4. Вывод формул перехода к цилиндрическим координатам 
.
5. Вывод определителя Якоби цилиндрических координат .
6. Вывод формул перехода к сферическим координатам:
.
Лекция № 6
1. Доказать, что замена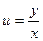 
сводит однородное уравнение к уравнению с разделяющимися переменными.
2. Вывести общий вид решения линейного однородного уравнения.
3. Вывести общий вид решения линейного неоднородного уравнения методом Лагранжа.
4. Доказать, что замена 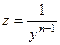сводит уравнение Бернулли к линейному уравнению.
Приложение 2.
Мелкие и устные вопросы на знание теории (для коллоквиумов).
Лекция № 1
1. Что такое первообразная и неопределённый интеграл, чем они отличаются?
2. Объяснить, почему 
тоже является первообразной.
3. Напишите формулу интегрирования по частям.
4. Какая замена требуется в интеграле вида 
и каким образом она устраняет корни?
5. Запишите вид разложения подынтегральной рациональной дроби на простейшие в случае, когда все корни различны и действительны.
6. Запишите вид разложения подынтегральной рациональной дроби на простейшие в случае, когда все корни действительны, и есть один кратный корень кратности k.
Лекция № 2.
|
|
|
1. Напишите, какое разложение рациональной дроби на простейшие в случае, когда в знаменателе есть множитель 2 степени с отрицательным дискриминантом.
2. Какая замена сводит интеграл к рациональной дроби?
3. Что такие универсальная тригонометрическая подстановка?
4. Какие замены производятся в случаях, когда функция под знаком интеграла нечётна относительно синуса (косинуса)?
5. Какие замены производятся в случае наличия в подынтегральной функции выражений 
, 
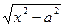, или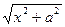 
.
Лекция № 3.
1. Определение определённого интеграла.
2. Перечислите некоторые из основных свойств определённого интеграла.
3. Напишите формулу Ньютона-Лейбница.
4. Напишите формулу объёма тела вращения.
5. Напишите формулу длины явно заданной кривой.
6. Напишите формулу длины параметрически заданной кривой.
Лекция № 4.
1. Определение несобственного интеграла (с помощью предела).
2. Чем отличаются несобственные интегралы 1 и 2 рода.
3. Приведите простые примеры сходящихся интегралов 1 и 2 рода.
4. При каких 
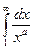
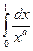сходятся интегралы (Т1).
5. Как сходимость связана с конечным пределом первообразной (Т2)
6. Что такое необходимый признак сходимости, его формулировка.
7. Признак сравнения в конечной форме
8. Признак сравнения в предельной форме.
9. Определение кратного интеграла.
Лекция № 5.
1. Смена порядка интегрирования, показать на простейшем примере.
2. Напишите формулу площади поверхности.
3. Что такое полярные координаты, напишите формулы перехода.
4. Чему равен якобиан полярной системы координат?
5. Что такое цилиндрические и сферические координаты, в чём их отличие.
6. Чему равен якобиан цилиндрических (сферических) координат.
Лекция № 6.
1. Что такое дифференциальное уравнение 1 порядка (общий вид).
2. Что такое дифференциальное уравнение 1 порядка, разрешённое относительно производной. Приведите какой-нибудь пример.
3. Что такое уравнение с разделяющимися переменными.
4. Что такое общее, частное решение, условия Коши.
5. Что такое однородное уравнение, каков общий метод его решения.
|
|
|
6. Что такое линейное уравнение, в чём состоит алгоритм его решения, что такое метод Лагранжа.
7. Что такое уравнение Бернулли, алгоритм его решения.
Приложение 3. Задачи из лекций.
Лекция № 1
Пример. 
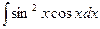. Пример. 
.
Пример. 
. Пример. 
.
Пример. 
Пример. 
.
Пример. 
. Пример. 
.
Лекция № 2
Пример. 
. Пример. 
.
Пример. 
. Пример. 
.
Пример. 
. Пример.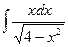 
.
Лекция № 3 
, 
, 
, 
, 
.
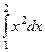Пример. Вычислить 
.
Пример. Найти площадь фигуры, ограниченной линиями 
.
Пример. Вывести формулу объёма шара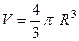 
.
Лекция № 4
Вычислить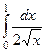 
, 
, 
, 
.
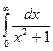Выяснить сходимость: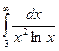 
, 
.
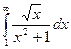Вычислить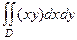 
, где 
есть квадрат: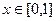 
, 
.
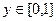Вычислить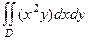 
, D треугольник с вершинами (0,0), (1,0), (1,1).
Лекция № 5.
Пример. Сменить порядок интегрирования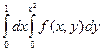 
.
Пример. Вычислить интеграл 
где D куб 
.
Пример. Вычислить интеграл 
где D - четверть круга единичного радиуса в первой четверти плоскости.
Пример. Доказать формулу площади круга 
с помощью полярных координат.
Пример. С помощью сферических координат вывести формулу объёма шара 
.
Лекция № 6.
Пример. Решить дифф. уравнение 
.
Пример. Решить дифференциальное уравнение 
.
Пример. Решить уравнение .
Пример. Решить уравнение .
Пример. Решить линейное уравнение .
|
|
|
