Распределение частот первичных оценок по тесту 6 глава

Один из путей устранения влияния тренировки на результаты оценки Н. р. — формирование устойчивого навыка в ра­боте с соответствующей методикой перед проведением тест-ретеста. Однако коли­чество повторений теста при этом неиз­бежно возрастает, что приводит к увели­чению числа запомнившихся решений. Такой прием может быть рекомендован для методик типа тестов скорости, со­держащих большое количество элементов тестового материала.

Для других методик, очевидно, един­ственным приемлемым путем снижения влияния тренировки остается увеличение интервала ретеста, что, однако, как уже говорилось выше, вступает в противоре­чие с определением надежности как ха­рактеристики теста.

Для большинства тестов общих спо­собностей характерно улучшение показа­телей Н. р. с возрастом испытуемых за счет лучшего контроля условий их выпол­нения. Другим фактором увеличения расчетных показателей Н. р. является отно­сительное замедление с возрастом темпа психического развития в области тех ха­рактеристик, которые могут стать объек­том измерения или влиять на результат теста. Благодаря этому, спустя время, со­ставляющее интервал ретеста, случайные колебания результатов обследования становятся менее выраженными. Это искус­ственно завышает показатели Н. р. Эта закономерность требует отдельных изме­рений Н. р. в разных возрастных контингентах испытуемых, что особенно суще­ственно для методик, предназначенных для обследования в широком возрастном диапазоне (см. Станфорд—Бине ум­ственного развития шкала, Векслера интеллекта измерения шкалы).

Указанные особенности и недостатки метода определения надежности путем ретеста делают его пригодным лишь для ограниченного числа методик, допускаю­щих многократное повторное обследова­ние. К их числу относятся сенсомоторные пробы, тесты скорости и ряд других мето­дик, отличающихся большим количеством пунктов (см. Миннесотский многоас­пектный личностный опросник).

НАДЕЖНОСТЬ ФАКТОРНО-ДИС­ПЕРСИОННАЯ — способ определения надежности, основанный на дисперси­онном анализе результатов теста. На­дежность теста соответствует отношению истинной дисперсии (т. е. дисперсии самого исследуемого фактора) к реально полученной эмпирической дисперсии. По­следняя складывается из истинной дис­персии и дисперсии погрешности изме­рения (см. Ошибка измерения). Фак­торно-аналитический подход к опреде­лению надежности дополнительно рас­членяет и дисперсию истинного показа­теля (Дж. Гилфорд, 1956).

Дисперсия истинного показателя, в свою очередь, может состоять из диспер­сии общего фактора для групп аналогич­ных тестов (см. Фактор G), особых фак­торов, обеспечивающих тесты специфи­ческой направленности (см. Факторы групповые) и дисперсии факторов, прису­щих конкретной тестовой методике. Сле­довательно, полная дисперсия теста рав­на сумме дисперсий для общих, специфических и единичных факторов плюс дис­персия погрешности:

 

где σ²_t — дисперсия теста, — дис­персия общих, групповых и единичных факторов, — дисперсия погрешности. Разделив уравнение на σ²_t получим:

 

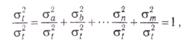
что может быть записано в виде:

 

где — доля дисперсии, выраженная об­щим фактором а, и т. д.

Таким образом, коэффициент надеж­ности теста равен:

 

Факторно-дисперсионный способ оп­ределения надежности подходит для оцен­ки уже факторизованного теста (см. Фак­торно-аналитический принцип), но не для тестов, измеряющих широкий набор разнообразных параметров, так как неко­торые из них могут не входить в установленную область валидности методики.

НАДЕЖНОСТЬ ЧАСТЕЙ ТЕСТА — характеристика надежности психодиаг­ностической методики, получаемая путем анализа устойчивости результатов от­дельных совокупностей тестовых задач или единичных пунктов (заданий) теста.

Наиболее простым и распространен­ным способом определения Н. ч. т. явля­ется метод расщепления, суть которого заключается в выполнении испытуемым заданий двух равноценных частей теста. Обоснованием метода является вывод о том, что при нормальном или близком к нормальному распределении оценок по полному тесту (см. Нормальное распре­деление) выполнение любого случайного набора из частей теста даст аналогичное распределение (при условии, что части однородны по характеру заданий по отно­шению к тесту в целом).

Для оценки надежности методом рас­щепления выбирают две эквивалентные по характеру и степени трудности группы задач (см. Внутренняя согласован­ность, Трудность заданий теста). Раз­деление объема заданий теста на сопоста­вимые части достигается:

— распределением заданий на четные и нечетные (в том случае, если задания в тесте строго ранжированы по степе­ни субъективной трудности);

— распределением пунктов по принципу близости или равенства значений ин­дексов трудности и дискриминативности (см. Дискриминативность зада­ний теста). Такой принцип разделения пригоден для тестов достижений, в которых обязателен ответ испытуе­мых на все пункты;

— распределением задач по времени ре­шения каждой из частей (для тестов скорости).

Для испытуемых в выборке определе­ния надежности (раздельно для каждой из частей теста) вычисляются оценки успеш­ности решений, среднеквадратические от­клонения первого и второго рядов оценок и коэффициенты корреляции сравнивае­мых рядов. Естественно, эти коэффици­енты будут характеризовать надежность лишь половины теста.

Уравнение Спирмена—Брауна отра­жает влияние изменения количества зада­ний на коэффициент надежности теста:

 

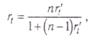
где r_t — коэффициент надежности для полного объема заданий, — его значе­ние после изменения числа заданий, п — отношение нового числа заданий к перво­начальному (если число заданий полного теста — 100, а его части, полученной ме­тодом расщепления на половины, — 50, то п = 0,5). Отсюда для полного теста:

 

Приведенные формулы справедливы для случаев равных стандартных отклоне­ний обеих половин теста (σ_х1 = σ_х2). Если σ_х1 отличается от σ_х2, для определения ко­эффициента надежности применяется формула Фланагана:

 

Этот же показатель для малых выборок рассчитывается по формуле Кристофа:

 

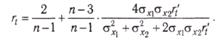
При определении r_t целого теста мож­но воспользоваться формулой Рюлона:

 

где 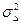— дисперсия разностей между ре­зультатами каждого испытуемого по двум половинам теста, — дисперсия сум­марных результатов. В данном случае ко­эффициент надежности рассчитывается как доля «истинной» дисперсии результа­тов теста (см. Надежность, Ошибка из­мерения).

При расщеплении тестов скорости применяется особая процедура группи­ровки заданий. Определяется минималь­ное время (t_min) решения целого теста, за­тем отсчитываются половина и четвертая часть этого времени. Все испытуемые ра­ботают половину минимального времени, после чего ставят отметку против зада­ния, выполняемого в момент подачи сиг­нала, и продолжают работать еще чет­верть минимального времени. Коэффици­ент надежности в этом случае будет соответствовать степени корреляции между числом задач, решенных до первого сигна­ла (0,5 t _min) и решенных за время между первым и вторым сигналами (0, 25t_mjn).

Разделение заданий теста на равно­ценные половины является лишь частным случаем Н. ч. т. Вполне возможно рас­щепление на три, четыре и более частей. В предельном случае число частей равно числу пунктов. При этом для определения надежности применяют анализ внутрен­ней согласованности.

При разделении всего набора заданий теста на любое количество групп для пра­вильного определения Н. ч. т., как уже указывалось выше, должно соблюдаться требование равноценности таких групп. Поэтому при вычислении коэффициента надежности методом анализа внутренней согласованности отобранные задания те­ста должны быть в высокой степени од­нородны по содержанию и трудности (го­могенны). При гетерогенных задачах значения r_t ниже истинных.

Наиболее распространенным методом оценки надежности отдельных заданий является вычисление коэффициента Кью­дера—Ричардсона:

 

где — дисперсия первичных оценок те­ста, р — индекс трудности, выраженный в виде доли — 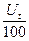- (см. Трудность заданий 100 теста), q = 1 - р, r_pb — коэффициент дискриминации (см. Дискриминатив-ность заданий теста).

В целях упрощения вычисления мо­жет быть применена формула Гуликсена:

 

где k — число заданий в тесте.

Это уравнение может быть упрощено следующим образом:

 

При отсутствии коэффициента диск­риминации применим вариант формулы Кьюдера—Ричардсона:

 

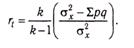
Пример вычислений r_t по методу Кью­дера — Ричардсона приведен в табл. 17.

 

Таблица 17

Определение коэффициента надежности методом Кьюдера—Ричардсона (n = 50; = 8,01; k = 16)

 

 

Предложенные выше формулы для оп­ределения коэффициента надежности при­годны для случаев, когда задания оцени­ваются в дихотомической шкале (см. Шка­лы измерительные) по принципу «выполнено — не выполнено». Для случаев с бо­лее дифференцированной оценкой приме­нима формула коэффициента альфа:

 

где 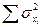— сумма дисперсий результатов отдельных заданий.

В практике психологической диагно­стики считается, что тест надежен, если r_t ≥ 0,6.

Коэффициент надежности обладает доверительным интервалом, определение которого особенно важно в связи с боль­шим количеством факторов, способных влиять на его значение. Доверительный интервал для r_t определяется как

 

где — стандартная ошибка коэффици­ента надежности — преобразование Фишера (определяется по статистическим таблицам). На практике применяется только нижняя граница r_t (Z_крит при γ = 0,05 составляет 1,96, при α = 0,01 -2,58).

Характеристика надежности по типу Н. ч. т. имеет серьезные преимущества по сравнению с надежностью ретестовой и надежностью параллельных, форм, главным образом благодаря отсутствию необходимости в повторном обследова­нии. Таким образом, снимается влияние многих посторонних факторов, в частно­сти тренировки, запоминания решений и т. д. Это обстоятельство определяет ши­рокое распространение методов характеристики Н. ч. т. по сравнению с другими типами надежности. К недостаткам мето­да относится невозможность проверить устойчивость результатов теста спустя определенное время. Это требует комби­нирования метода Н. ч. т. с другими типа­ми характеристики надежности психоло­гической методики.

«НАРИСУЙ ИСТОРИЮ» (Draw-a-Story, DAS) — проективная методика иссле­дования личности. Предложена Р. Силвером в 1987 г. Предназначена для раннего обнаружения депрессии, в частности — скрытой депрессии.

«Н. и.» основывается на обычных для проективных методик положениях: а) дет­ское восприятие одних и тех же рисунков различно; б) на восприятие оказывает влияние личный опыт; в) рисунки могут отражать элементы личности, поддающи­еся квантификации.

В методике комбинируются исследо­вательские процедуры разных проектив­ных техник. Первоначально обследуемый должен выбрать из 14 картин две и по ним придумать историю (на предлагаемых кар­тинах в основном содержатся изображе­ния людей и животных). Затем необходи­мо сделать рисунок по мотивам ранее во­ображенной истории. Наконец, предлага­ется записать историю. Темы рисунка и истории оцениваются по 7-балльной шка­ле (от «выражение негативная» до «выраженно позитивная»). Негативные темы содержат указания на «грусть», «печаль», «смерть», «беспомощность», «будущее без надежд на лучшее» и т. п. и рассматрива­ются как знаки депрессии.

«Н. и.» предназначена для группового обследования детей и подростков, начи­ная с 5-летнего возраста. Сообщается о высокой надежности методики. Так, на­дежность ретестовая (интервал ретеста — неделя) при обследовании детей с эмоциональными расстройствами — 0,87.

Данные о валидности ограниченны, тем не менее имеются сведения о том, что темы депрессивных детей и подростков оцениваются в основном как «выражение негативные», чего не наблюдается в других группах. Имеются нормативные дан­ные, полученные при обследовании 380 детей и подростков, однако они не могут быть признаны репрезентативными.

Сведений об использовании в СНГ нет.

«НАРИСУЙ ЧЕЛОВЕКА» ТЕСТ (Draw-A-Person Test, DAP) — проективная ме­тодика исследования личности. Разрабо­тана К. Маховер в 1948 г. на основе теста Ф. Гудинаф, предназначенного для опре­деления уровня интеллектуального разви­тия детей и подростков с помощью выпол­ненного ими рисунка мужчины (см. Гуди­наф «Нарисуй человека» тест).

«Н. ч.» т. можно использовать для об­следования как взрослых, так и детей, до­пускается групповое обследование.

Обследуемому предлагают каранда­шом на чистом листе бумаги нарисовать человека. После выполнения рисунка ему дают задание нарисовать человека проти­воположного пола. Заключительный этап обследования — опрос. К. Маховер со­ставлены специальные перечни вопросов о нарисованных фигурах. Эти вопросы ка­саются возраста, образования, семейного положения, привычек и т. д.

При интерпретации полученных дан­ных автор исходит из идеи о том, что ри­сунок является выражением «Я» обследу­емого. Значительное внимание уделяется анализу разнообразных деталей рисунка, прежде всего особенностям изображения основных частей тела, которые зачастую оценивают в соответствии с психоанали­тической символикой. Изучение валидно­сти «Н. ч.» т. западными психологами привело к противоречивым результатам в силу умозрительности предлагаемых ав­тором интерпретаций. Имеются данные о том, что общие субъективные оценки бо­лее валидны и надежны, нежели оценки по отдельным деталям рисунка.

В СССР «Н. ч.» т. первоначально при­менялся в клинико-психологических ис­следованиях. Анализировались преиму­щественно формальные аспекты рисун­ков, напр, размер фигуры, ее расположе­ние на листе бумаги, степень законченно­сти рисунка и т. п. (Ю. С. Савенко, 1970). Полученные при обследовании пациента результаты соотносились с клинической картиной заболевания, обогащая и уточ­няя представление о больном. Начиная с 90-х годов сфера использования теста су­щественно расширяется, выполнено не­мало исследований в возрастной и педаго­гической психологии.

НАРУШЕНИЙ ПСИХИЧЕСКОЙ АДАПТАЦИИ ОПРОСНИК (НПА) - опросник личностный, разработан А. И. Скорик и Л. С. Свердловым в 1993 г. Предназначен для предварительной диаг­ностики адаптационных нарушений.

Методика носит скрининговый харак­тер (см. Отсеивание). Исследование, проводимое при помощи НПА, позволяет получить общее представление о наличии или отсутствии проявлений психической дезадаптации, их основных особенностях. Требования,предъявляемые к такого рода ускоренной диагностике, обусловили не­большой объем опросника и простоту об­работки первичных данных.

Опросник НПА состоит из 37 утверж­дений, касающихся личностных качеств и психологических особенностей испытуе­мого, состояния соматической сферы, представлений о психическом здоровье, восприятия некоторых обыденных жизненных проблем. Задания опросника тре­буют только утвердительных или отрица­тельных ответов («да»—«нет», «верно»— «неверно», «согласен»—«не согласен»). Ответ «не знаю» не допускается. Опросник может применяться при индивидуаль­ном и групповом обследовании. Оценки первичные подсчитываются в соответ­ствии с «ключом», раздельно по 6 шкалам опросника. Особенностью первичной об­работки является то, что подсчитывается не просто число совпадений с ключом с оценкой 1 балл за каждое совпадение, а суммируются удельные веса каждого из совпавших с ключевым значением отве­тов (см. Внутренняя согласованность). Весовая величина каждого пункта рассчи­тывалась на основе определения фактор­ной нагрузки (см. Факторный анализ) данного ответа в измеряемом шкалой при­знаке. Расчет сделан таким образом, что веса пунктов выражаются целыми числа­ми от 1 до 9. Сырые оценки переводятся в стандартные Т-баллы (см. Оценки шкаль­ные). Результаты представляются графи­чески на специальном бланке в виде оце­нок профильных.

Шкалы опросника разработаны на ос­нове результатов факторного анализа первичного статистического материала, полученного в соответствующих клини­ческих группах испытуемых: 1. (В) Опи­сывает переживание общего физического и психического комфорта. В норме у адап­тированных испытуемых оценка по дан­ной шкале имеет тенденцию к повыше­нию. 2. (Н) Шкала «ипохондрии» — отра­жает степень фиксации на соматическом неблагополучии. При нарушениях адапта­ции оценка по данной шкале повышается. 3. (М) Шкала «гипоманиакальности» — фиксирует ощущение комфорта с оттен­ком эйфории, «форсированного благопо­лучия», беспечности. При нарушении адаптации оценка снижается. 4. (Р) Шка­ла описывает депрессивное состояние. Результат отрицательно коррелирует с данными по шкале М. В норме наблюда­ется низкая оценка. 5. (N) Шкала «невротизации» — описывает состояние эффек­тивно-вегетативного дисбаланса, возникающего при эмоциональном напряжении, «нервозность». При нарушениях адапта­ции оценка повышается. 6. (S) Шкала фиксирует нарушения в сфере соци­альных отношений. У дезадаптированных оценка повышается.

При интерпретации данных НПА ос­новное значение имеет анализ «профиля». Наряду с этим авторы предлагают про­стые формальные критерии диагностики дезадаптации. Простейшим из них являет­ся критерий, основанный на высоте про­филя. Дезадаптация имеет место в том случае, если оценки хотя бы двух шкал превышают значения 70 Т или опускают­ся ниже 30 Т либо одна из шкал превыша­ет 80 Т или опускается ниже 20 Т. По дан­ным авторов, вероятность необнаружения реально существующей дезадаптации со­ставляет лишь 5%. Однако вероятность того, что достаточно адаптированные лица будут причислены к дезадаптирован­ным, составляет 22,5%. Это делает дан­ный критерий малопригодным, в частно­сти при проведении массовых эпидемио­логических исследований. Более слож­ным и точным (10% вероятности того, что адаптированные будут причислены к дезадаптированным) является критерий, учи­тывающий дифференцированный резуль­тат по «шкалам благополучия» (В, М) и «шкалам неблагополучия» (Н, D, N, S). Дезадаптация диагностируется в тех слу­чаях, когда В + М составляют 79 Т или когда сумма Н, D, N и S превышает 255 Т. Сравнительные исследования на матери­але контрастных групп показали высо­кую корреляцию комплексного критерия дезадаптации с верифицированным диаг­нозом (r = 0,85, Р< 0,001).

Надежность ретестовая НПА (при интервале ретеста 1 сутки) по различным шкалам колеблется в интервале r_t = 0,74-0,90. Имеются сведения о валидности текущей, которая изучалась путем сопоставления данных контрастных групп (группы психически здоровых адекватно адаптированных, психически здоровых с нарушениями адаптации и больных с неврозоподобными состояниями). Сведения о надежности и валидности опросника НПА дают основание предполагать эф­фективность методики в индивидуальном и массовом скрининге состояний психи­ческой дезадаптации.

НЕСУЩЕСТВУЮЩЕЕ ЖИВОТ­НОЕ — проективная методика иссле­дования личности; предложена М. 3. Друкаревич.

Испытуемому предлагают придумать и нарисовать несуществующее животное, а также дать ему ранее не существовавшее имя. Из имеющейся литературы видно, что процедура обследования не стандар­тизована (используются разных размеров листы бумаги для рисования, в одних слу­чаях рисунок выполняется цветными ка­рандашами, в других — одним цветом и т. д.). Общепринятой системы оценки ри­сунка не существует. Теоретические по­сылки, положенные в основу создания ме­тодики, совпадают с таковыми у прочих проективных методик. Как и многие дру­гие рисуночные тесты, Н. ж. направлен на диагностику личностных особенностей, иногда ее творческих потенций.

Показана удовлетворительная валидность конвергентная методики путем установления связи между результатами, полученными с ее помощью, и данными других личностных методик на материале обследования пациентов психиатричес­кой клиники и лиц, проходящих профот­бор в штат МВД (П. В.Яньшин, 1988, 1990). Валидность также подтверждена при дифференциации больных неврозами и здоровых (Т. И. Краско, 1995). Н. ж. — одна из наиболее популярных рисуночных методик и широко используется психоло­гами СНГ при обследовании детей и взрослых, больных и здоровых чаще всего в качестве ориентирующей методики, т. е. такой, данные которой позволяют выдвинуть некоторые гипотезы об особен­ностях личности.

НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ — вид распределения переменных. Н. р. наблюдается при изменении призна­ка (переменной) под влиянием множества относительно независимых факторов. График уравнения Н. р. представляет со­бой симметричную унимодальную колоколообразную кривую, осью симметрии ко­торой является вертикаль (ордината), проведенная через точку 0 (рис. 46).

 

Рис. 46. Процентное распределение случаев под нормальной кривой

Кривая Н. р. была построена для про­стого аппроксимативного решения задачи вероятности частот событий. Нормальная кривая описывается формулой де Муавра

 

 

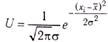
U — высота кривой над каждым за­данным значением x_i, — среднее арифметическое x_i, 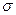— среднеквадратическое отклонение от .

Теоретически существует бесконечное множество нормальных кривых с кон-летными значениями М и σ. При стандартизации тестовых оценок и в некоторых других случаях используется Н. р. со следующими характеристиками: М = 0; σ= 1; площадь под нормальной кривой равна единице. Такое распределе­ние носит название стандартного (единич­ного) Н. р. Для любого Н. р. в пределах значений х₁. М + σ лежит около 68%, в пределах М ± 2σ — 95%, М ± 3σ — 99,7% площади под кривой. Частоты слу­чаев, укладывающихся в интервалы, огра­ниченные значениями от М ± σ до М ± σ, составляют 68,26%; 95,44%; 99,72%; 99,98 % соответственно (рис. 46). Высо­та кривой (U) над значением М приблизи­тельно равна 0,3989. Асимметрия стан­дартной, как и любой другой нормальной, кривой равна нулю, эксцесс (Q) — трем (см. Оценка типа распределения). Рас­пределение показателей, получаемых в эмпирических психологических и психо­диагностических исследованиях при боль­шом числе наблюдений, как правило, при­ближается к Н. р.

На практике важную роль имеет вы­числение площади слева от любой точки на оси абсцисс, ограниченной участком нормальной кривой и ординатой этой точки. Так как площадь стандартного Н. р. равна единице, то доля этой площа­ди отражает частоту случаев с х_i, мень­шими, чем данное значение на оси X. Ре­шение уравнения де Муавра для любого значения х неудобно, поэтому для опре­деления площади слева от данного зна­чения в различных Н. р. (по оси z) име­ются специальные таблицы (см. табл. 1 Приложения III).

Важнейшим качеством Н. р. является то, что для семейства нормальных кривых характерны одинаковые доли площадей, лежащих под участками, ограниченными равными значениями σ. При этом любую нормальную кривую можно свести к еди­ничной и таким образом ответить на во­прос о площади между выбранными точками на кривой или высоте кривой над любой из точек оси X. Форма нормальной кривой не изменяется при вычитании среднего значения и делении на σ. Так, если нужно выяснить, какая часть площади лежит слева от значения х = 20 в Н. р. с = 25 и 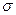= 5, эту задачу можно заменить вы­яснением площади, лежащей слева от в единичном Н. р. Для стандартного Н. р. значение х указывает, что точка отстоит от среднего на х единиц. Отклонение значения от среднего х — , а число стандартных отклонений, которое отделяет х от , составляет 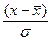- единичное нормальное отклонение (z). Рассмотренная выше закономерность обобщается правилом: если х имеет нор­мальное распределение со средним и стандартным отклонением 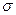, то - характеризуется нормальным распределением со средним 0 и стандарт­ным отклонением 1. Площадь между x_l и в Н. р. со средней и стандартным от­клонением 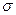равна площади между и в единичном Н. р.

Предположим, результаты измерения IQ-показателей в выборке с достаточно большим числом обследованных (п) обла­дают свойствами нормального распреде­ления. Значение = 4,52, σ = 3, тогда в точке со значением IQ-показателя 10,4 . Для этого значения площадь слева от z составит 0,975 (97,5%). Это означает, что лишь у 2,5% испытуемых оценки IQ превышают 10,4. Можно определить, какое число членов выборки укладывается в интервал оценок от 10,4 до 8,3. Тогда .

Площадь слева от z для этого значения составит 0,1020 (10,2%). Следовательно, число лиц, имеющих оценку ниже 8,3, составляет 89,8%, а число лиц с оцен­кой в интервале 8,3-10,4 составляет 97,5-89,8 = 7,7%.

Число случаев в пределах стандартно­го отклонения можно легко определить без расчетов. Так, в интервале оценок, со­ответствующих -2 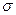и - 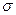, находится 13,6% обследованных (см. рис. 46).

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: