Поверхностные явления и адсорбция

Объекты, изучаемые дисциплиной «Поверхностные явления и дисперсные системы» обладают двумя основными признаками: гетерогенностью и дисперсностью.

Гетерогенность или многофазность является качественным признаком, обеспечивающим наличие межфазной поверхности, поверхностного слоя.

В гетерогенных системах на границе раздела фаз существует переходный (межфазный) слой, в котором постепенно меняются свойства и структура при переходе от одной фазы к другой. Межфазный слой обладает набором собственных термодинамических свойств, зависящих от различия свойств образующих его фаз. Молекулы этого слоя втягиваются в соседние фазы с разной интенсивностью, что создает натяжение вдоль поверхности раздела, которое называют поверхностным натяжением на границе раздела конденсированная фаза - газ и межфазным на границе конденсированных фаз. Увеличение этой границы требует затраты энергии по переводу молекул из глубины фазы (более глубокой потенциальной ямы) на поверхность раздела, что эквивалентно избытку свободной энергии, которое является интенсивной величиной, а площадь поверхности раздела s - экстенсивной. Следовательно, общая свободная поверхностная энергия на любой границы раздела будет равна

(1.1)

Дисперсность или раздробленность является количественным признаком изучаемой дисциплины. Применяются следующие количественные параметры раздробленности: размер частиц а, дисперсность D, удельная поверхность s_уд. В зависимости от формы частицы берется ее характеристический размер: для сферы – диаметр d, для куба – ребро l.

Между этими характеристиками существуют простые соотношения.

D = 1 / а, м^-1 (1.2)

Удельную поверхность можно рассчитать по размеру частиц дисперсной фазы:

, м^-1, (1.3)

где V – объем частиц дисперсной фазы; К – коэффициент формы частиц; d – диаметр частицы.

Для сферических частиц

(1.4)

Поверхностные явления выражаются в том, что состояние находящихся в поверхностном слое молекул иное по сравнению с молекулами, находящимися в объеме тела. Молекулы в объеме тела равномерно окружены такими же молекулами, и поэтому их силовые поля полностью скомпенсированы. Взаимодействие молекул в поверхностном слое происходит в несимметричном силовом поле. Равнодействующая межмолекулярных сил, действующих на молекулу, находящуюся в поверхностном слое, не равна нулю и направлена внутрь той фазы, с которой взаимодействие больше. Таким образом, возникает поверхностное натяжение s, стремящееся сократить поверхность.

Поверхностное натяжение можно представить и как энергию переноса молекул из объема тела на поверхность или как работу образования единицы поверхности. Поверхностное натяжение можно выразить частной производной от энергии Гиббса по величине межфазной поверхности при р и Т = const (при постоянных числах молей компонентов):

(1.5)

Отсюда следует, что для индивидуального вещества поверхностное натяжение есть энергия Гиббса, приходящаяся на единицу поверхности.

Одними из наиболее распространенных методов измерения поверхностного натяжения являются сталагмометрический и тензиометрический методы. Сталагмометрический метод основан на том, что в момент отрыва капли от нижнего конца вертикальной трубки вес капли уравновешивается силой поверхностного натяжения. Величину поверхностного натяжения рассчитывают по формуле:

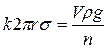, (1.6)

где r – внутренний радиус трубки, k – константа прибора, V – объем расширенной части сталагмометра, ρ – плотность жидкости, n – число капель.

В случае относительного определения s расчет проводят по формуле:

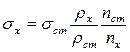(1.7)

При измерении s методом отрыва кольца (тензиометрическим) расчет проводят по формуле:

(1.8)

где φ_х и φ_сm – углы закручивания стальной нити весов при которой происходит отрыв кольца для измеряемой и стандартной жидкости соответственно.

Внутренняя (полная) энергия поверхностного слоя U_s (в расчете на единицу площади) связана с s уравнением Гиббса – Гельмгольца:

(1.9)

Одним из распространенных поверхностных явлений является адсорбция – процесс выравнивания химических потенциалов компонентов между поверхностью и объемом, приводящий к изменению концентрации на поверхности.

Количественными характеристиками адсорбции являются:

Гиббсовская адсорбция - избыточная концентрация i–го компонента, рассчитанная на единицу площади поверхности.

(1.10)

Другой характеристикой адсорбции является поверхностная концентрация адсорбата α, равная общей концентрации вещества в поверхностном слое, рассчитанной на единицу площади поверхности и выражаемой в моль/м².

Когда поверхность адсорбента неизвестна, величину адсорбции измеряют емкостью поверхностного слоя А и выражают в моль/г.

Адсорбция на границе раствор – газ описывается адсорбционным уравнением Гиббса для разбавленных растворов:

(1.11)

где 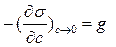называют предельной поверхностной активностью, являющейся характеристикой взаимодействия молекул растворителя и растворенного вещества.

Связь между поверхностным натяжением и составом раствора для ПАВ и разбавленных растворов выражается уравнением Шишковского:

(1.12)

где s₀ – поверхностное натяжение чистого растворителя;

В – константа, мало зависящая от природы ПАВ;

1/A – удельная капиллярная постоянная;

с – концентрация ПАВ.

Принимая разность s₀ –s за поверхностное (двухмерное) давление π, получим уравнение состояния идеального двухмерного газа:

(1.13)

Адсорбцию на различных границах раздела фаз описывают уравнением мономолекулярной адсорбции Ленгмюра:

или (1.14)

где А_max - максимальная адсорбция, К – константа адсорбционного равновесия, с - концентрация адсорбата, р – давление пара адсорбата. Для определения констант А_max и К изотерму часто представляют в виде уравнения в линейной форме

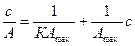(1.15)

Различают также полимолекулярную адсорбцию газов и паров на твердом адсорбенте, которая описывается изотермой БЭТ:

(1.16)

где С – постоянная, равная отношению констант равновесия мономолекулярной адсорбции и конденсации пара; р/p_s – относительное давление пара; А_max - ее максимальная величина, соответствующая полному заполнению монослоя (модель Ленгмюра).

Расчет констант А_max и С осуществляется путем спрямления экспериментальной зависимости А = f(p/p_s) в координатах линейной формы:

(1.17)

К поверхностным явлениям также относятся адгезия, когезия, смачивание и растекание.

Адгезия характеризуется величиной работы адгезии, определяемой по формуле Дюпре:

(1.18)

где s₂₁ - поверхностное натяжение твердого тела или жидкости 2 на границе раздела с газом 1, s₃₁ – то же на границе твердого тела 3 с газом 1, s₃₂ - на границе двух конденсированных фаз 2 и 3.

Если одна или две фазы жидкие, то условие равновесия жидкости на поверхности твердого тела или другой жидкости можно характеризовать косинусом краевого угла смачивания по формуле Юнга:

(1.19)

Поскольку нет надежных методов определения поверхностного натяжения на границе раздела твердое – газ, твердое - жидкость, работу адгезии выражают объединенным уравнением Дюпре – Юнга:

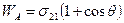(1.20)

Работа когезии (взаимодействие в однородной фазе) выражается через удвоенное поверхностное натяжение:

(1.21)

Растекание жидкости по поверхности твердого тела или другой жидкости определяется коэффициентом растекания Гаркинса:

(1.22)

Если f >0, нанесенная на поверхность жидкость растекается; если f <0 - увеличивает первоначальный краевой угол (собирается в каплю).

 

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

1. При конденсации тумана, состоящего из капель кадмия, образовалось 12,5^.10^-6 м³ жидкого кадмия. Поверхностное натяжение при температуре конденсации равно 570 мДж/м². Свободная поверхностная энергия всех капель кадмия составляла 53 Дж. Вычислите дисперсность и диаметр капель жидкого кадмия.

РЕШЕНИЕ Энергия Гиббса поверхности определяется по уравнению (1.1):

Связь между удельной поверхностью S_УД, поверхностью S, объемом V и дисперсностью D выражаются соотношениями (1.3) и (1.4):

Поверхность капель тумана составляет .

Дисперсность капель кадмия равна

Диаметр капель кадмия равен .

 

2. Рассчитайте полную поверхностную энергию 10 г эмульсии гексана в воде с концентрацией 70% мас. и дисперсностью D = 1мкм^-1 при температуре 298 К. Плотность гексана при этой температуре 655 кг/м³, поверхностное натяжение 18,41 мДж/м², температурный коэффициент поверхностного натяжения dσ/dT = -0,104 мДж/м².

РЕШЕНИЕ Полная поверхностная энергия рассчитывается по уравнению Гиббса-Гельмгольца (1.9):

.

Поверхность s капель бензола 70% эмульсии массой 10 г составляет:

 

3. Используя константы уравнения Шишковского В = 0,173; А = 0,046, определите, при какой концентрации поверхностное натяжение водного раствора масляной кислоты при 293К будет равно 68.12·10^-3 Н/м. Поверхностное натяжение воды 7,253·10^-2 Н/м.

РЕШЕНИЕ Согласно уравнению Шишковского (1.12)

25,5 с + 1 = 1,423, отсюда с = (1,423-1)/25,5 = 1,96·10^-2 кмоль/м³

 

4. Вычислите адсорбцию валериановой кислоты на поверхности раздела водного раствора с воздухом при 353К и концентрации с =2,9·10^-3 кмоль/м³, если константы уравнения Шишковского в этом случае равны В =0,28; А =0,05 кмоль/м³; σ ₀ = 63·10^-3Н/м.

РЕШЕНИЕ Константы уравнения Шишковского связаны с константами уравнения Ленгмюра следующим образом:

,

Рассчитываем константы уравнения Ленгмюра

К = 1/0,05 = 20 м³/ кмоль

Рассчитываем адсорбцию по уравнению Ленгмюра

 

5. Вычислите толщину адсорбционного слоя церотиновой кислоты (С₂₅Н₂₁СООН), адсорбированной из бензольного раствора на поверхности воды. Площадь, занимаемая молекулой ПАВ в насыщенном адсорбционном слое, равна 0,25 нм², плотность ρ равна 0,836·10³ кг/м³.

РЕШЕНИЕ. Зная площадь, занимаемую молекулой ПАВ в насыщенном слое, рассчитываем величину предельной адсорбции Г _max:

Толщину адсорбционного слоя вычисляем по уравнению:

 

6. Удельная поверхность непористой сажи равна 73,7 м²/кг. Рассчитайте площадь, занимаемую молекулой бензола в плотном монослое, исходя из данных об адсорбции бензола на этом адсорбенте при 293 К.

 

р, Па 1,03 1,29 1,74 2,50 6,67

A ·10² , моль/кг 1,57 1,94 2,55 3,51 7,58

Предполагается, что изотерма адсорбции описывается уравнением Ленгмюра.

Используя уравнение Ленгмюра в координатах линейной формы (1.15):

рассчитывают значения p/А:

p/А ·10², Па·кг/моль 0,656 0,668 0,68 0,712 0,879

и строят график в координатах p/А – f (p)

 

Риc.1. Изотерма адсорбции бензола в координатах линейной формы уравнения Ленгмюра.

 

Из графика находят:

Удельная поверхность адсорбента связана с емкостью слоя A_max соотношением

Площадь, занимаемая молекулой бензола в плотном монослое, равна

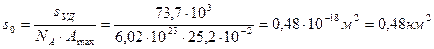
7. По приведенным данным рассчитайте (по БЭТ) удельную поверхность адсорбента по изотерме адсорбции бензола на твердой поверхности. Площадь, занимаемая одной молекулой бензола, s_о =49×10^-20 м²:

p/p_s 0,024 0,05 0,14 0,20 0,265 0,35

А ×10³

кмоль/кг 0,0149 0,0348 0.0472 0,0566 0,0663 0,0799

РЕШЕНИЕ. Используя уравнение БЭТ в координатах линейной формы (1.17):

,

рассчитываем величину:

1650 1512 3449 4417 5438 6739

и строим зависимость

 

Риc.2. Изотерма адсорбции бензола в координатах линейной формы уравнения БЭТ.

Получим из графика: , , С =16,9, А _max=5,7^.10^-5 моль/кг.

 

8. Вычислите константу скорости адсорбции оксиэтилированного спирта RO(CH₂CH₂O)₈H, (R - разветвленный алкил С₁₀) на ткани из водных растворов (концентрация раствора 1,0 г/л, Т = 303 К) по следующим экспериментальным данным:

τ, мин
А ∙107,моль/м2	3,3	3,6	3,7	3,72

РЕШЕНИЕ. Рассчитывают значения (А_р – А_τ), lg(А_р – А_τ) и строят график зависимости lg(А_р – А_τ) от времени адсорбции. Константа скорости адсорбции равна отрицательному значению тангенса тупого угла наклона прямой к оси абсцисс, tgθ = -0.147 K = - tgθ/0.434 = 0.147/0.434 = 0.339 мин^-1

 

Рис.3. Определение константы скорости адсорбции.

 

9. Рассчитайте работу адгезии в системе вода-графит, зная, что краевой угол равен 90°, а поверхностное натяжение воды составляет 71,96 мДж/м². Определите коэффициент растекания воды на графите.

РЕШЕНИЕ. Работа адгезии по уравнению Дюпре – Юнга (1.20) равна:

Работа когезии равна:

Коэффициент растекания рассчитывается по соотношению:

¦ = W_A - W_К = 71,96 - 143,92 = -71,96 мДж/м², т.е. вода не растекается по графиту.

 

 

12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: