 |
Оптические свойства дисперсных
|
|
|
|
СИСТЕМ
Результаты исследования оптических свойств дисперсных систем имеют большое значение для изучения их структуры, определения размеров и формы частиц, а также концентрации.
В зависимости от оптических свойств частицы и от соотношения между размером частицы и длиной волны света в дисперсных системах могут наблюдаться прохождение света через систему, преломление и отражение света частицами дисперсной фазы, рассеяния света и абсорбция (поглощение) света дисперсной фазой.
Для наноразмерных систем, частицы которых меньше длины волны видимой части спектра, характерны рассеяние и абсорбция света.
Интенсивность света, рассеянного единицей объема разбавленной системы со сферическими, непроводящими электрический ток частицами, размер которых мал по сравнению с длиной волны падающего света, выражается уравнением Рэлея:
(4.1)
где Jр и J0 - интенсивности рассеянного и падающего света; n - число частиц 1 м3 золя (частичная концентрация);
V - объем отдельной частицы, м3; n0 и n1 - показатели преломления дисперсной фазы и дисперсионной среды; l - длина волны падающего света.
Уравнение Рэлея применимо дня частиц, размер которых составляет не более 0,1 длины световой волны, т.е. для частиц не больше 40-70 нм. Для частиц большего размера Jр изменяется обратно пропорционально не четвертой, а меньшей степени l.
Если для данного золя обозначить
то уравнение (4.1) запишется
(4.2)
В уравнении (4.1) можно ввести объемную концентрацию дисперсной фазы с об. В этом случае уравнение Рэлея принимает вид:
(4.3)
Отношение интенсивности рассеянного света к интенсивности падающего света называют мутностью
(4.4)
Уравнение Рэлея является основой оптических методов исследования растворов по светорассеянию: ультрамикроскопии, нефелометрии, турбидиметрии и электронной микроскопии.
|
|
|
Истинные растворы поглощают свет в соответствии с законом Бугера - Ламберта - Бера:
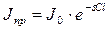(4.5)
где J0 – интенсивность падающего света; Jпр - интенсивность прошедшего света; c - концентрация; l - толщина слоя; e - молярный коэффициент поглощения.
(4.6)
Одной их характеристик поглощения света является оптическая плотность
(4.7)
В золях ослабление пучка света может происходить за счет поглощения и рассеяния света. Тогда уравнение (4.5) принимает вид:
(4.8)
где k - коэффициент ослабления света вследствие рассеяния (фиктивной абсорбции) света.
Для определения размера коллоидных частиц с помощью ультрамикроскопа через определенные промежутки времени подсчитывают число частиц n в определенном объеме V сильно разбавленного золя. Частичная концентрация равна n = n / V. Если известны плотность дисперсной фазы ρ и весовая концентрация с, то объем частицы V = с / ρ ∙ n. Принимая форму частиц шарообразной, можно рассчитать средний радиус частиц:
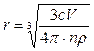(4.9)
Среднюю длину ребра кубической частицы равна:
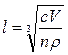(4.10)
При нефелометрическом методе исследования золей измеряют интенсивность рассеянного света, падающего на кювету с дисперсной системой. Рассеяние исследуемого раствора сравнивают с рассеянием стандартного раствора, размер частиц или концентрация которого известны.
Весовую концентрацию золя или его дисперсность определяют следующим образом. Кюветы с золями освещают равномерно падающим светом и меняя высоту освещенной части золей h1 в h2 добиваются равенства интенсивности света, рассеянного обоими золями. При этом должно соблюдаться равенство
(4.11)
При одинаковой концентрации золей размер частиц исследуемого золя рассчитывают по формуле
(4.12)
При одинаковом размере частиц золей концентрацию исследуемого золя рассчитывают по формуле
|
|
|
(4.13)
Метод турбидиметрии основан на измерении интенсивности проходящего через дисперсную систему света. Рассеянный свет можно считать фиктивно поглощенным, и поэтому можно считать, что закономерности рассеяния света подчиняются закону Бугера - Ламберта - Бера
(4.14)
J пр = τ = К ∙ с об ∙ V ∙ Jо (4.15)
Измеряют оптическую плотность наноразмерных систем при различных концентрациях и определяют графически величину (τ/ с об)с→0. Объем сферической частицы рассчитывают по формуле: V = τ / с об ∙ К
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
1. Раствор золя золота с концентрацией с =5∙10-5 кг/м3 исследован с помощью ультрамикроскопа. Число частиц в поле зрения площадью 1∙10-6 м2 и глубиной пучка света 2∙10-2 м равно n = 6,5. Предполагая, что частицы золота сферические, вычислите их средний радиус. Плотность золота 19,3∙103 кг/м3.
РЕШЕНИЕ Объем раствора в поле зрения микроскопа составляет 
. Численная концентрация n золя золота составляет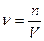 
. Объем одной частицы золя золота составляет: 
Радиус сферической частицы рассчитывается по формуле (4.9):
2. Вычислите среднее значение молярного коэффициента поглощения при прохождении света (длина волны 470 нм) через слой коллоидного раствора гидроокиси железа различной концентрации с при разной толщине слоя l. Данные опытов приведены ниже:
Концентрация с, % 0,10 0,05 0,04 0,02
Толщина слоя l ٠10-3, м 2,5 2,5 5,0 5,0
J прошедшего света, % 5,9 10,9 11,0 32,5
РЕШЕНИЕ Для вычисления молярного коэффициента поглощения применим уравнение Бугера - Ламберта - Бера в логарифмической форме (4.6)
или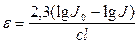 
Подставим численные значения для с = 0,1%; Jпр = 5,9%; l = 2,5·10-3 м
Аналогично рассчитываем ε 2 = 11,15∙103; ε 3 = 11,04∙103; ε 4 = 11,19∙103; ε ср = 11,17∙103.
|
|
|
