 |
А1. Предварительные сведения
|
|
|
|
Электрической цепью называют систему, состоящую из источников электрической энергии (источников питания), приёмников (потребителей) и соединяющих их электрических проводов, вдоль которых энергия от источника передаётся потребителю. Источники питания, провода и потребители являются основными элементами электрической цепи. Кроме основных электрические цепи содержат дополнительные элементы в виде приборов, оборудования и аппаратуры, обеспечивающих контроль и управление режимами работы цепи в целом и её элементов.
Источники питания образуют внутреннюю часть электрической цепи, а потребитель совместно с соединительными проводами, приборами, выключателями и т.д. – внешнюю часть.
Если электрическая цепь замкнута, то по ней проходит электрический ток. Его прохождение по цепи связано с процессами непрерывного преобразования энергии в каждом из её элементов:
- в источниках питания имеет место преобразование в электрическую энергию других видов энергии: механической энергии в электрическую в генераторах, химической в электрическую в гальванических элементах и аккумуляторах, тепловой – в термоэлементах, лучистой – в фотоэлементах и т.д.;
- в приёмниках происходит обратное преобразование электрической энергии в другие виды энергии: в механическую в двигателях, в тепловую в нагревательных устройствах, в световую в источниках света и химическую в аккумуляторах и установках различных отраслей промышленности.
В источниках питания в процессе преобразования каких-либо видов энергии в электрическую возбуждается электродвижущая сила (ЭДС), которая вызывает в замкнутой цепи электрический ток. Участки цепи, содержащие ЭДС, называют активными, а без ЭДС – пассивными. Для удобства изображения, анализа и расчёта электрические цепи при графическом изображении представляются в виде схем замещения, которые называются электрическими схемами. Эти схемы состоят из отдельных условно изображённых реальных элементов, соединённых тем или иным образом. Схема замещения является расчётной моделью реальной цепи.
|
|
|
Электрические цепи в зависимости от ряда характерных для них признаков подразделяются на группы и имеют свои наименования. Так, цепи, по которым проходят постоянные токи, называются электрическими цепями постоянного тока. Если электрическое сопротивление цепи не зависит от проходящего по нему тока, то такие цепи называются линейными электрическими цепями. В этих цепях каждый элемент имеет вольтамперную характеристику (т.е. зависимость U = f (I)) в виде прямой линии. Если вольт-амперная характеристика элемента цепи непрямолинейна, то такой элемент называется нелинейным. Электрические цепи, в которые входит хотя бы один нелинейный элемент, называют нелинейными.
В зависимости от числа приёмников электрической энергии, числа источников питания и способа их соединений различают электрические цепи простые (или неразветвлённые) и сложные (или разветвлённые), цепи с одним источником питания и цепи с несколькими источниками питания.
На рис. А.1 приведена схема простой (т.е. неразветвлённой) электрической цепи постоянного тока с одним источником питания.
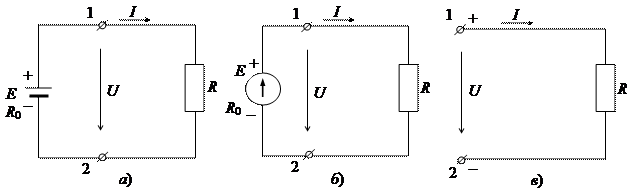
Рис. А.1. Схема неразветвлённой электрической цепи
с одним источником питания
Элементами схемы А.1 а являются аккумулятор (или гальванический элемент) с ЭДС Е и внутренним сопротивлением R 0 и приёмник с сопротивлением R. Сопротивление соединительных проводов пренебрежимо мало и поэтому не учитывается в данном случае. На рис. А.1. б изображена такая же простейшая цепь, в которой источник питания – генератор постоянного тока с ЭДС Е и внутренним сопротивлением R 0.
|
|
|
На схемах указаны положительные направления ЭДС (Е), напряжения (U) и тока (I). На схеме А.1 а знаками «+» и «–» обозначена полярность внешних зажимов источника. Напомним, что электрический ток – это направленное движение электрических зарядов. На внешнем пассивном участке ток направлен от положительного полюса источника к отрицательному, а внутри источника – от точек низшего потенциала (т.е. от «–») к точкам высшего потенциала (т.е. к «+»).Перенос зарядов во внешней цепи происходит под действием электрического поля в проводнике, а перемещение их в источнике возможно только за счёт сил неэлектрического происхождения, называемых сторонними силами. Интенсивность сторонних сил характеризуется значением ЭДС. Сторонние силы, как уже называлось, могут быть обусловлены химическими процессами (в гальванических элементах и аккумуляторах) и др.
Таким образом, стрелка, обозначающая положительное направление ЭДС, направлена от минуса к плюсу, а стрелка, обозначающая положительное направление напряжения, – от плюса к минусу. За положительное направление тока также выбрано направление от точки высшего потенциала к точке низшего потенциала (т.е. от плюса к минусу).
В реальных электрических цепях потребители не присоединяются непосредственно к зажимам источника. Они подключаются к зажимам 1 и 2. На эти зажимы электрическая энергия подаётся от источника по электропроводам, которые в схеме обычно не показывают (рис. А.1 в).
Работа реальных электрических элементов цепи характеризуется определёнными величинами, связанными с их токами, напряжениями, ЭДС и мощностями. Поэтому задачей анализа и расчёта электрической цепи является установление связи между ЭДС, напряжениями, токами и параметрами цепи. При этом параметрами цепей постоянного тока в установившемся режиме являются их сопротивления R (единица измерения [Ом]) и проводимости G (единица измерения – сименс [См]).
Важными понятиями, характеризующими топологические свойства электрических цепей и необходимыми для их анализа, являются понятия узла, ветви и контура /9/.
Узлом (точкой разветвления) называют точку электрической цепи, в которой соединяется 3 или более проводников (ветвей).
|
|
|
Ветвь – это участок цепи без разветвлений между двумя соседними узлами, по которому проходит один и тот же ток.
Контур – замкнутый путь по ветвям схемы. Существуют важные понятия независимого и зависимого контура.
Элементы электрических цепей могут соединяться последовательно или параллельно. При последовательном соединении элементов по ним проходит один и тот же ток, поэтому в пределах ветви ток один и тот же. Таким образом, в любой электрической цепи токов столько, сколько ветвей.
Параллельным называют такое соединение, при котором две или более ветвей присоединены к двум узлам, отличающимся друг от друга потенциалами.
Смешанным соединением элементов цепи называют сочетание их последовательных и параллельных соединений. Например, на рис. А.2 приведена схема разветвлённой цепи постоянного тока со смешанным соединением её элементов.
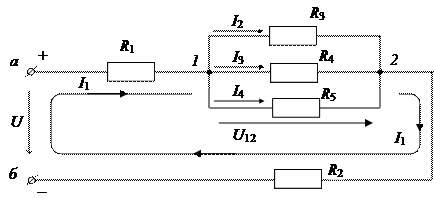 |
Рис. А.2. Электрическая схема разветвлённой цепи постоянного тока
Схема рис. А.2 содержит 4 ветви. В первой ветви, по которой протекает ток I 1, соединяются последовательно: сопротивление R 1, источник питания с напряжением U на его зажимах а и б и сопротивление R 2. Между точками 1 и 2 с напряжением U 12 включены три параллельные ветви, каждая со своим сопротивлением (R 3, R 4 и R 5) и соответственно с токами I 2, I 3, I 4. Элементы первой ветви соединены последовательно с участком 1-2, образуя таким образом схему смешанного соединения.
Основными законами, устанавливающими соотношения между ЭДС, напряжениями, токами и сопротивлениями, являются закон Ома и I и II законы (правила) Кирхгофа. С помощью этих законов можно провести анализ и расчёт любых электрических цепей. Так в неразветвленной схеме рис. А.1 а, б под действием ЭДС Е будет возникать ток I, значение которого определяется законом Ома:
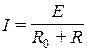 ,
,
где Е – ЭДС источника;
R 0– внутреннее сопротивление источника.
Для участка электрической цепи, сопротивление которого R и напряжение на котором U, закон Ома записывается в виде
|
|
|
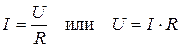 .
.
Произведение I·R называют падением напряжения. Таким образом, напряжение на любом пассивном участке электрической цепи (т.е. не содержащем ЭДС) равно произведению тока участка на сопротивление этого участка.
Сложные (т.е. разветвлённые) схемы можно рассчитывать с помощью законов Кирхгофа, которые являются следствием закона сохранения энергии.
По первому закону Кирхгофа алгебраическая сумма токов в узле (точке разветвления) электрической цепи равна нулю.
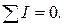
При этом токи, направленные к узлу, следует брать с одним (произвольно выбранным) знаком, а токи, направленные от узла, – с противоположным знаком.
Для узла «1» рис. А.2 уравнение I закона Кирхгофа можно записать в виде
I 1 – I 2 – I 3 – I 4 = 0
или
I 1 = I 2 + I 3 + I 4 ,
что позволяет I закон сформулировать так: сумма токов, направленных к узлу, равна сумме токов, направленных от узла.
Уравнения II закона Кирхгофа записываются для контуров электрической цепи. Согласно II закону Кирхгофа в замкнутом контуре алгебраическая сумма падений напряжений на элементах этого контура равна алгебраической сумме ЭДС
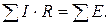
При составлении уравнений по II закону Кирхгофа произвольно намечаются направления обхода контуров, при этом положительными считаются те ЭДС, направления которых совпадают с направлением обхода контура, а падения напряжения считаются положительными на тех участках, на которых совпадают направление тока (напряжения) и направление обхода контура.
Напишем уравнения II закона Кирхгофа для контуров схемы рис. А.2, обходя их по часовой стрелке
для контура 2, R 2, б, а, R 1, R 3, 2:
I 1· R 2 – U + I 1· R 1 + I 2· R 3 = 0;
для контура 1, R 3, 2, R 4, 1:
I 2· R 3 – I 3· R 4 = 0;
для контура 1, R 4, 2, R 5, 1:
I 3· R 4 – I 4· R 5 = 0.
|
|
|


