 |
Основные производственные показатели предприятий электросвязи
|
|
|
|
| Номер предприятия | Чистая прибыль, тыс. руб. | Численность обслуживаемого населения, млн. чел | Рентабельность, % |
| у | х1 | х2 | |
| 4,9 | |||
| 5,1 | |||
| 6,5 | |||
| 3,7 | |||
| 4,0 | |||
| 2,5 |
В качестве результативного признака возьмем чистую прибыль у. Основные факторы, влияющие на ее формирование: численность населения, обслуживаемого предприятием электросвязи х1, и рентабельность х2 Линейная форма зависимости между признаками постулируется, и, следовательно, задача сводится к отысканию параметров уравнения:
 .
.
При линейной форме связи множественный корреляционно-регрессионный анализ проводится на основе информации о средних значениях признаков 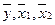 , их средних квадратических отклонениях
, их средних квадратических отклонениях  и парных коэффициентах корреляции
и парных коэффициентах корреляции  .
.
Построим уравнение двухфакторной регрессии в стандартизированном масштабе и рассчитаем показатели тесноты связи (табл. 2.2).
Таблица 2.2
Расчетная таблица для определения параметров уравнения регрессии
| у | х1 | х2 | (х1)2 | (х2)2 | х1 х2 | у х1 | у х2 | у2 |
| 4,9 | 24,0 | |||||||
| 5,1 | 26,0 | |||||||
| 6,5 | 42,3 | |||||||
| 3,7 | 13,7 | |||||||
| 4,0 | 16,0 | |||||||
| 2,5 | 6,3 | |||||||
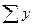 = = 960 = = 960
|  = 26,7
= 26,7
|  = 117
= 117
|  = 128,3
= 128,3
| 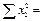 = 2411
= 2411
|  = = 501 = = 501
|  = 4419 = 4419
|  = 19537
= 19537
|  = =173646 = =173646
|
Используя итоги расчетной таблицы (см. табл. 2.2) и известные формулы для расчета средних, дисперсий и парных коэффициентов корреляции:



 ,
,  .
.
вычислим показатели, необходимые для отыскания  -коэффициентов:
-коэффициентов:
 = 160 тыс. руб.,
= 160 тыс. руб.,  у = 57,8 тыс. руб.;
у = 57,8 тыс. руб.;
 = 4,45 млн. чел.,
= 4,45 млн. чел.,  = 1,2513 млн. чел.;
= 1,2513 млн. чел.;
 = 19,5%,
= 19,5%,  = 4,6458%;
= 4,6458%;
 0,3392,
0,3392,  0,5071,
0,5071,  - 0,5806.
- 0,5806.
|
|
|
Система нормальных уравнений в стандартизированном виде может быть записана так:
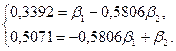
Решая эту систему, находим:  = 0,9558,
= 0,9558,  2 = 1,062. Таким образом, можно записать уравнение регрессии в стандартизированном виде:
2 = 1,062. Таким образом, можно записать уравнение регрессии в стандартизированном виде:
ty = 0,9558t1 + 1,062t2.
Коэффициенты при tj показывают, что большее воздействие на чистую прибыль предприятия электросвязи оказывает рентабельность ( 2 >
2 >  ). С ее ростом на сигму при постоянной численности обслуживаемого населения чистая прибыль увеличивается на 1,062 своего среднего квадратического отклонения.
). С ее ростом на сигму при постоянной численности обслуживаемого населения чистая прибыль увеличивается на 1,062 своего среднего квадратического отклонения.
Переход от стандартизированного уравнения регрессии к уравнению регрессии в натуральном масштабе осуществляется по формулам:
 .
.
Найдем параметры искомого уравнения:
 ;
;
 ;
;
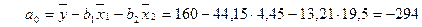 .
.
Уравнение зависимости чистой прибыли предприятий электросвязи от численности обслуживаемого населения и рентабельности имеет вид: 
Оно показывает, что с ростом численности обслуживаемого населения на 1 млн. чел., при исключении влияния второго фактора (рентабельности), чистая прибыль возрастает на 44,15 тыс. руб., а при неизменной численности населения с ростом рентабельности на 1% чистая прибыль повысится на 13,21 тыс. руб.
Коэффициент множественной детерминации для нашего примера окажется равным:
 =0,8627.
=0,8627.
Отсюда коэффициент множественной корреляции 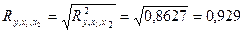 .
.
Полученные значения коэффициентов множественной корреляции и детерминации, близкие к 1, свидетельствуют о том, что при построении двухфакторной модели учтены важные факторы увеличения чистой прибыли. При дополнительном включении факторов в анализ (для данного числа предприятий) может увеличиться совокупный коэффициент детерминации и, соответственно, уменьшиться остаточная дисперсия, доля которой в нашем примере мала:
 0,8627 = 0,1373.
0,8627 = 0,1373.
Следовательно, на долю неучтенных факторов приходится не более 13,73% дисперсии результативного признака.
Эластичность по каждому фактору и по их совокупности составит:
|
|
|


 =2,84.
=2,84.
Эластичность по каждому фактору и в целом по совокупности больше 1, значит, чистая прибыль увеличивается в большей степени, чем факторы. С увеличением каждого фактора на 1% следует ожидать увеличения чистой прибыли на 2,84%.
Практическое занятие разработано:
к.т.н., профессор Дмитриев Я.В., к.т.н. Зуев А.С.
«___»_________2012 г.
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ
Кафедра «Экономические информационные системы»
УТВЕРЖДАЮ
Заведующий кафедрой ЭФ-2
_________________ Лагунова А.Д.
«____»_____________2012г.
Для студентов факультета ЭФ
специальности 080801
к.т.н., профессор Дмитриев Я.В., к.т.н. Зуев А.С.
(ученая степень, ученое звание, фамилия и инициалы автора)
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
(Методические рекомендации)
|
|
|


