Премиальные фонды и прибыли предприятий

№ предприятия	Премиальный фонд (у. е.)	Прибыль (у. е.)

Решение. Для проведения регрессионного анализа составим таблицу со вспомогательными расчетами.

Расчет сумм для проведения регрессионного анализа

№ (i)	y	x	x 2	x 3	x 4	x 5	x 6	1/x	1/x 2
			1,00×106	1,00×109	1,00×1012	1,00×1015	1,00×1018	1,00×10-3	1,00×10-7
			1,44×106	1,73×109	2,07×1012	2,49×1015	2,99×1018	8,33×10-4	6,94×10-7
			1,69×106	2,20×109	2,86×1012	3,71×1015	4,83×1018	7,69×10-4	5,92×10-7
			1,21×106	1,33×109	1,46×1012	1,61×1015	1,77×1018	9,09×10-4	8,26×10-7
			1,00×106	1,00×109	1,00×1012	1,00×1015	1,00×1018	1,00×10-3	1,00×10-6
			8,10×105	7,29×108	6,56×1011	5,90×1014	5,31×1017	1,11×10-3	1,23×10-6
			1,44×106	1,73×109	2,07×1012	2,49×1015	2,99×1018	8,33×10-4	6,94×10-7
			1,00×106	1,00×109	1,00×1012	1,00×1015	1,00×1018	1,00×10-3	1,00×10-6
			1,69×106	2,20×109	2,86×1012	3,71×1015	4,83×1018	7,69×10-4	5,92×10-7
			1,44×106	1,73×109	2,07×1012	2,49×1015	2,99×1018	8,33×10-4	6,94×10-7
			1,00×106	1,00×109	1,00×1012	1,00×1015	1,00×1018	1,00×10-3	1,00×10-6
			8,10×105	7,29×109	6,56×1011	5,90×1014	5,31×1017	1,11×10-3	1,23×10-6
Итого			1,45×107	1,64×1010	1,87×1013	2,17×1016	2,55×1019	1,12×10-2	1,06×10-5

(Продолжение)

Расчет сумм для проведения регрессионного анализа

№ (i)
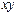
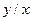
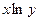
	6,90	47,72	4,61	1,00×105	1,00×108	1,00×1011	0,10	4,61×103	31,81	690,78
	7,09	50,27	5,01	1,80×105	2,16×108	2,59×1011	0,13	6,01×103	35,53	1063,51
	7,17	51,41	5,30	2,60×105	3,38×108	4,39×1011	0,15	6,89×103	37,99	1434,02
	7,00	49,04	5,01	1,65×105	1,82×108	2,00×1011	0,14	5,51×103	35,09	1050,46
	6,91	47,72	4,61	1,00×105	1,00×108	1,00×1011	0,10	4,61×103	31,81	690,78
	6,80	46,27	3,91	4,50×104	4,05×107	3,65×1010	0,06	3,52×103	26,61	340,12
	7,09	50,27	4,87	1,56×105	1,87×108	2,25×1011	0,11	5,84×103	34,51	921,71
	6,91	47,72	4,25	7,00×104	7,00×107	7,00×1010	0,07	4,25×103	29,35	483,54
	7,17	51,41	5,30	2,60×105	3,38×108	4,39×1011	0,15	6,89×103	37,99	1434,02
	7,09	50,27	3,40	3,60×104	4,32×107	5,18×1010	0,03	4,08×103	24,11	212,70
	6,91	47,72	5,01	1,50×105	1,50×108	1,50×1011	0,15	5,01×103	34,61	1036,16
	6,80	46,27	4,79	1,08×105	9,72×107	8,75×1011	0,13	4,31×103	32,57	816,29
Итого	83,85	586,09	56,06	1,63×106	1,86×109	2,16×1012	1,31	6,15×104	391,98	10174,1

 

Составим системы нормальных уравнений по каждой из моделей:

1. Линейная:

2. Параболическая:

3. Кубическая:

4. Гиперболическая:

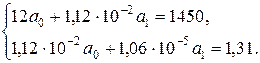
5. Показательная:

6. Степенная:

7. Логарифмическая:

 

Представленные системы линейных уравнений можно решить различными методами (подстановок, Крамера, Жордана-Гауса, обратной матрицы). Найденные коэффициенты регрессии и сами уравнения представлены в таблице.

Коэффициенты регрессии

№	Вид модели	Коэффициенты регрессии	Уравнение регрессии
a 0	a 1	a 2	a 3
	Линейная	-103,45	0,21	–	–
	Параболическая	839,19	-1,53	7,89 10-4	–
	Кубическая	-11324	32,2917	-0,0303	9,44 10-6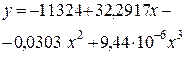
	Гиперболическая	337,01	-232241	–	–
	Показательная	22,44	1,0014	–	–
	Степенная	0,0024	1,53	–	–
	Логарифмическая	-1414,8	219,77	–	–

 

Для определения той из моделей, которая наиболее точно описывает зависимость двух показателей, необходимо подсчитать суммы квадратов их отклонений и определить минимальное из полученных значений. Подробный расчет по линейной модели приведен в первой таблице, во второй таблице представлены данные по всем рассматриваемым моделям регрессии.

Расчет суммы квадратов отклонений по линейной модели

№	y	x
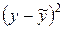
			106,55	-6,55	42,90
			148,55	1,45	2,10
			169,55	30,45	927,20
			127,55	22,45	504,00
			106,55	-6,55	42,90
			85,55	-35,55	1263,80
			148,55	-18,55	344,10
			106,55	-36,55	1335,90
			169,55	30,45	927,20
			148,55	-118,55	14054,10
			106,55	43,45	1887,90
			85,55	34,45	1186,80
Итого	22518,90

Сумма квадратов отклонений для рассматриваемых моделей

№	Вид модели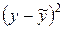
	Линейная	22518,90
	Параболическая	20692,15
	Кубическая	17136,71
	Гиперболическая	22972,93
	Показательная	25415,03
	Степенная	24912,61
	Логарифмическая	22595,40

Как видно из последней таблицы, наименьшее отклонение наблюдается при кубической модели, поэтому можно считать, что она наиболее точно описывает зависимость между премиальным фондом и прибылью предприятий. Графически данная зависимость представлена на рис. 3.3.

Рис. 3.3. Зависимость между прибылью и премиальным фондом.

 

2-й учебный вопрос: решение задач по множественному регрессионному анализу.

Рассмотрим методику корреляционно-регрессионного анализа на примере статистической обработки данных по предприятиям электросвязи

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: