 |
Для проведения практического занятия № 4 и № 5
|
|
|
|
По дисциплине «Эконометрика»
ТЕМА « Решение задач по парной регрессии »
ТЕМА « Решение задач по множественной регрессии »
Обсуждена на заседании кафедры
(предметно-методической секции)
«15»мая 2012 г.
Протокол № 11
МГУПИ – 2012 г.
1. Тема практического занятия №4 и №5: решение задач по парной и множественной регрессии.
2. Учебные и воспитательные цели:
1. Выработать практические умения, а также приобрести навыки решения задач по парному регрессионному анализу.
2. Выработать практические умения, а также приобрести навыки решения задач по множественному регрессионному анализу.
3. Выработать практические умения, а также приобрести навыки оценки результатов применения регрессионного анализа.
3. Время: 4 часа (180 минут).
4. Место проведения: специализированная аудитория.
5. Литература для подготовки (основная и дополнительная):
а) Основная литература:
1. Федосеев В.В., Гармаш А.Н., Орлова И.В. и др. / Экономико-математические методы и прикладные модели: Учебное пособие для вузов / Москва / ЮНИТИ-ДАНА / 2012
2. Васильева Э.К., Лялин В.С. / Статистика: Учебник для студентов вузов, обучающихся по специальностям экономики и управления (080100) / Москва / ЮНИТИ-ДАНА / 2012
3. Буравлев А.И. Эконометрика: доп. УМО в кач. учеб. пособия для вузов. — М.: Бином. Лаборатория знаний, 2012
б) Дополнительная литература:
1. Колемаев В.А., Гатауллин Т.М., Заичкин Н.И. и др. / Математические методы и модели исследования операций: Учебник для студентов вузов, обучающихся по специальности 080116 «Математические методы в экономике» и другим экономическим специальностям / Москва / ЮНИТИ-ДАНА / 2012
2. Балдин К.В., Башлыков В.Н., Рукосуев А.В. / Основы теории вероятностей и математической статистики: Учебник / Москва / Флинта / 2010
|
|
|
6. РАСЧЕТ УЧЕБНОГО ВРЕМЕНИ:
Вступительная часть — до 5 минут (напомнить содержательные постановки задач применения методов регрессионного анализа).
Основная часть (учебные вопросы) — до 170 мин.
1-й учебный вопрос: решение задач по парному регрессионному анализу — 80 минут.
2-й учебный вопрос: решение задач по множественному регрессионному анализу — 90 минут.
Заключительная часть — до 5 минут.
С О Д Е Р Ж А Н И Е
| Содержание занятия (указания и рекомендации по методике проведения) | Время (в мин.) |
| Вступительная часть: - проверить наличие студентов по докладу старосты; - проверить наличие журнала группы, правильность записи темы занятия, отметить отсутствующих, поставить свою подпись; - раскрыть содержание ПЗ; - довести целевую установку через учебные вопросы ПЗ; - вскрыть особенности практической работы студентов на ПЗ. | До 5 |
| Основная часть — рассмотрение учебных вопросов: (в процессе выполнения работы отвечать на индивидуальные вопросы студентов с целью разъяснения вызвавших затруднения моментов) 1-й учебный вопрос:решение задач по парному регрессионному анализу — 80 минут. 2-й учебный вопрос: решение задач по множественному регрессионному анализу — 90 минут. Заключительная часть: - подведение итогов занятия; - оценить учебную деятельность студентов; - собрать файлы с решениями примеров; - ответить на вопросы студентов. | До 170 До 5 |
8. Приложения: приведенный далее текст с материалами распечатки содержания практического занятия и состава вариантов.
1-й учебный вопрос: решение задач по парному регрессионному анализу.
По группе предприятий, выпускающих один и тот же вид продукции, рассматривается функция издержек 
. Необходимая для расчета оценок параметров информация представлена в таблице 1.1.
|
|
|
Таблица 1.1
Расчетная таблица
| Номер предприятия | Выпуск продукции, тыс. ед. х | Затраты на производство, млн. руб. у | 
| 
| 
| 
|
| 331,1 67,9 141,6 104,7 178,4 104,7 141,6 | ||||||
| Итого |
Система нормальных уравнений будет иметь вид:
Решив ее, получим:
.
Уравнение регрессии примет вид:
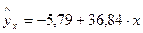
Подставив в уравнение значения х, найдем теоретические значения у. В данном случае параметр 
не имеет экономического смысла.
По данным, приведенным в таблице, требуется провести регрессионный анализ, используя следующие модели: линейную, параболическую, кубическую, гиперболическую, показательную, степенную, логарифмическую. Определить, какая из моделей точнее описывает зависимость между прибылью предприятия и его премиальным фондом. Наилучшую зависимость представить на графике, отобразив на нем исходные данные.
|
|
|
