 |
Истечение газа через сопла, форсунки.
|
|
|
|
При постоянных давлениях в резервуаре (трубе) Р1 и за соплом, Р2 объемный расход газа определяется:
, (2.4.9)
где DР- перепад давлений; eР – коэффициент расширения:
, где К – показатель адиабаты. (2.4.10)
6. Свободная струя -поток, не ограниченный твердыми стенками.
Различают струи:
-затопленные – в среде с теми же физическими свойствами (вода в воде).
-незатопленные – в другой среде (вода в воздухе).
Струя подразделяется на 3 характерные части:
- компактная (ядро) – сохраняется цилиндричность струи и начальная скорость.
- раздробленная - сплошность нарушается, струя расширяется. Угол расширения зависит от степени турбулентности струи.
- распыленная – наблюдается окончательный распад на отдельные капли.
Координаты осевой линии незатопленной струи, вытекающей из насадка в горизонтальном направлении, определяются:
, (2.4.11)
где Х -дальность боя (падения); Y- высота падения струи.
Для струи, вытекающей со скоростью u под углом a к горизонту, теоретическая дальность полета определяется:
, максимальная дальность при a = 45°: 
(2.4.12)
Для реальных условий: 
- формула Гавырина, (2.4.13)
где d – диаметр насадка; Н – напор на выходе из насадка.
Для вертикальной струи теоретическая высота подъема: 
(2.4.14)
Взаимодействие потока и твердых тел.
При обтекании твердых тел потоком жидкости возникают гидравлические сопротивления двух видов: за счет сил трения и за счет разности сил давлений перед и за обтекаемым телом. Соотношение между этими силами зависит от формы тела и направления движения потока.
1) Обтекание плоской тонкой пластинки, установленной вдоль потока. Сопротивление определяется, в основном, силами трения.
Сила сопротивления трения при обтекании тела конечной длины равна:
|
|
|
, (2.4.15)
где F- площадь обтекаемой поверхности;
СT –средний по длине коэффициент сопротивления трения:
При одностороннем обтекании: При двухстороннем:
(2.4.16)
2) Поверхность пластины установлена по нормали к потоку.
Сопротивление обуславливается, в основном, разностью давлений.
Сила сопротивления давления определяется:
. (2.4.17)
СД - коэффициент сопротивления давления. К-т зависит от размеров и формы поверхности.
3) Обтекание тела произвольной формы
Силы вязкости и силы давления соизмеримы и должны учитываться обе.
Распределение давления по контуру тела определяется экспериментально и учитывается аэродинамическим коэффициентом К:
р = К r u2/2. (2.4.18)
Сила давления на любую грань определяется:
Рд = р. S, где S – площадь вертикальной проекции грани.
Суммарное сопротивление трения и давления называется лобовым сопротивлением. Сила лобового сопротивления:
, (2.4.19)
где СХ – коэффициент лобового сопротивления.
Силу активного давления струи, вытекающей из сопла (насадка) на неподвижную поверхность (грань) можно определить по выражению:
, (2.4.20)
где w-сечение струи (сопла); a - угол, на который отклоняется струя при взаимодействии с преградой.
Для плоской вертикальной поверхности a = 90° и (1- cos a) =1.
Истечение через водосливы.
Расход жидкости определяется:
, (2.4.21)
где Н – напор на водосливе (высота жидкости над гребнем водослива).
m - коэффициент расхода. Для различных типов водосливов коэффициент приводятся в справочной литературе.
Для прямоугольного незатопленного водослива шириной В:
(2.4.22)
Коэффициент расхода можно определить по эмпирической формуле:
, (2.4.23)
где Р – высота стенки.
Для треугольного водослива с углом 90°:
(2.4.24)
Расчет затопленных водосливов ведется по тем же формулам с учетом уменьшающего коэффициента затопления.
УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ.
|
|
|
Задачи на истечение через отверстия, насадки, сопла можно решать, как правило, без записи уравнения Бернулли, используя основное выражение (2.4.2). Расчетный напор истечения в общем случае состоит из суммы геометрического и пьезометрического напора: Н = Z + (P/rg). Движение жидкости при опорожнении резервуаров (переменный напор) в каждый данный момент времени рассматривается как установившееся.
Коэффициент расхода m однозначно определяется коэффициентами сжатия e и скорости j (сопротивления z).
Истечение через сужающие устройства в трубопроводах происходит в ту же среду, т.е. представляет собой истечение через затопленное отверстие.
ПРИМЕРЫ.
Пример 2.4.1. Определить коэффициент сопротивления многоступенчатой диафрагмы, отнесенный к скорости в трубке диаметром d = 10 мм. Каждая ступень представляет собой отверстие dO = 2 мм в стенке толщиной 1 мм. Коэффициент расхода отверстия m = 0,62. Считать, что взаимное влияние отверстий отсутствует, а полные потери между ступенями распределяются поровну. Определить полную потерю давления при скорости в трубке u = 1 м/с, плотность жидкости r = 850 кг/м3.
Решение.
Потери давления DР в одной ступени можно выразить из основного соотношения (2.4.2): 
, откуда 
Расход через каждое отверстие равен расходу в трубке:
Q = wu = 
Находим потери давления в 5 ступенях:
Так как истечение происходит через тонкую стенку (dO > d), то сопротивление обусловлено только местными сопротивлениями. Коэффициент сопротивления диафрагмы находим из формулы Вейсбаха для определения потерь давления в местных сопротивлениях (см. тему 3):
, откуда 
.
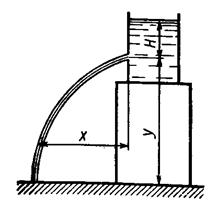Пример 2.4.2. При истечении жидкости через отверстие d = 10 мм измерены: расстояние Х =5,5 м, высоты Y = 4 м, Н = 2 м, расход Q = 0,305 л/с. Не учитывая сопротивления воздуха, определить коэффициенты сжатия, скорости, расхода и сопротивления.
Решение.
По выражению (2.4.11) дальность боя и высота падения струи связаны соотношением: , откуда находим коэффициент скорости:
.
Из основного выражения (2.4.2) определяем коэффициент расхода:
Из соотношения ej = m определяем коэффициент сжатия:
Коэффициент сопротивления без учета сопротивления воздуха находим из выражения (2.4.1) для определения коэффициента скорости
|
|
|
откуда 
.
Пример 2.4.3. Струя воды (r = 1000 кг/м3), вытекая из полости с давлением 11,8 ат в атмосферу через круглое отверстие диаметром d = 0,15 м c острыми кромками, ударяется о вертикальную пластину, Определить нормальную составляющую силы давления на пластину.
Решение.
Сила воздействия струи в направлении оси определяется по (2.4.20). Для вертикальной плоской пластины
Принимая коэффициент расхода равным 0,62, по формуле (2.4.2) находим расход воды через отверстие:
Находим скорость струи:
u = Q/w = 4Q/pd2 = 4 . 0,53 / 3,14 . 0,152 = 30 м/с
Находим силовое воздействие на пластину
РДА = 1000 . 0,53 . 30 . 1= 15900 Н =15,9 кН
Тема 2.5. ГИДРАВЛИЧЕСКИЙ РАСЧЕТ НАПОРНЫХ ТРУБОПРОВОДОВ.
Напорные трубопроводы - отдельные или соединенные между собой трубы, по которым под принудительным давлением транспортируются жидкости или газы.
Трубопроводы различают:
1. По соотношению потерь напора:
- короткие – местные потери напора составляют более 10% от потерь напора по длине, hM > 0,1 hl
- длинные – местные потери менее 10% от линейных, hM < 0,1 hl;
2. По гидравлической схеме:
- простые – без ответвлений и без раздачи расхода по пути движения;
- сложные – состоящие из магистрали и ответвлений, через которые происходит раздача.
3. По надежности работы:
- тупиковые(разомкнутые) – жидкость поступает в узел только по одному направлению;
- кольцевые(замкнутые) - жидкость поступает в узел по двум или более направлениям.
Экономическая скорость, uэ. – скорость движения жидкости в трубопроводе, обеспечивающая минимальные приведенные затраты, т.е. оптимальное соотношение эксплуатационных и капитальных затрат. Значение uэ зависит от назначения трубопроводных систем.
Экономически выгодный диаметр, dэ – диаметр трубопровода, соответствующий экономической скорости.
При расчете напорных трубопроводов для определения потерь напора по длине используются 3 метода:
1. По гидравлическому уклону i: 
(2.5.1)
Гидравлический уклон i определяется по формулам темы 3 данного раздела.
2. По удельному сопротивлению трубопровода А (сопротивление 1м данного трубопровода):
|
|
|
для турбулентного режима: 
(2.5.2)
(2.5.3)
для ламинарного режима: 
(2.5.4)
(2.5.5)
Для практического использования значения А рассчитаны для старых и новых труб из различных материалов (приводятся в таблицах).
Методы 1,2 применяются для расчета напорных труб круглого сечения.
Универсальный метод расчета для напорного и безнапорного движения любой геометрической формы сечения потока:
3. По модулю расхода К: 
(2.5.6)
Расходная характеристика К выражает пропускную способность (расход) по трубе из данного материала при гидравлическом уклоне, равном 1. Для стандартных диаметров составлены таблицы.
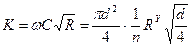(2.5.7)
где R – гидравлический радиус; С, м0,5/с - коэффициент Шези
(2.5.8)
Показатель степени (y) можно принять приближенно:
При R< 1 y = 1,5 n0,5; при R > 1 y = 1,3 n0,5.
Для не старых стальных труб можно принять у = 1/6.
n – коэффициент шероховатости труб (справочные данные). При отсутствии данных коэффициент n можно определить из приближенной зависимости
кЭ = (80n)6;
Скорость движения жидкости определяется по формуле Шези
(2.5.9)
Для турбулентного режима величина К может быть принята по таблицам.
При ламинарном режиме расходная характеристика определяется по формуле
(2.5.10)
где А – коэффициент в формуле (3.5).
|
|
|
