Тема 1. 3. Давление на криволинейные поверхности.

 

Сила давления на криволинейную цилиндрическую стенку есть геометрическая сумма ее горизонтальной F_Х и вертикальной F_Y составляющих:

(1.3.1)

Горизонтальная составляющая F_Х равна силе давления жидкости на плоскую вертикальную проекцию цилиндрической поверхности, т.е. определяется по формуле (1.2.1).

Вертикальная составляющая F_Y силы давления на стенку шириной В равна весу жидкости в воображаемом жидком теле (теле давления).

F_Y = ± G_ТД = ± r g V_ТД = ± r g S_ТД B (1.3.2)

Поперечное сечение тела давления S_ТД представляет собой фигуру, заключенную между самой цилиндрической поверхностью, горизонтом жидкости (или его продолжением) и вертикалями, восстановленными из конечных точек поверхности до горизонта жидкости. Тело давления, полученное в результате построения со смоченной стороны поверхности – положительное (+), с не смоченной – отрицательное (-). В последнем случае направление действия силы F_Y противоположно направлению действия силы тяжести. Точка приложения F_Y совпадает с центром тяжести жидкого тела.

Направление действия равнодействующей силы определяется углом наклона a вектора равнодействующей из треугольника с катетами F_X, F_Y.

Центр давления, т.е. точка приложения силы F находится графическим построением, исходя из следующего правила: вектор равнодействующей силы, направленный под углом a, проходит через точку пересечения направлений действия горизонтальной и вертикальной составляющих силы давления.

УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ

Для решения задач на определение силы давления на криволинейную цилиндрическую поверхность необходимо:

- определить горизонтальную составляющую силы давления F_Х, как силу давления на вертикальную плоскую проекцию этой поверхности по формулам, приведенным в темах 1.1 и 1.2.

- построить поперечное сечение тела давления согласно правилам, описанным в данной теме, определить вес жидкости в теле давления и направление действия вертикальной составляющей F_Y (см. пример 1.3.2);

- по (1.3.1) определить величину равнодействующей силы F;

- определить центры приложения сил F_Y, F_х и обозначить векторами;

-определить графоаналитическим способом точку приложения равнодействующей силы, т.е. центр давления по описанному выше правилу (см. пример1.3.3).

ПРИМЕРЫ

Пример 1.3.1. Построить эпюру горизонтальной составляющей силы избыточного давления жидкости на трубу при высоте жидкости h₁ и h₂.

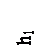
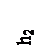
Решение. Горизонтальная составляющая силы избыточного гидростатического давления есть сила избыточного давления на вертикальные проекции ab и bc поверхностей АВ и ВС, т.е. избыточное давление выражается треугольниками давления, построенными по формуле (1.1.3) Р = r g h. Эпюры давления строятся отдельно для стенки ab и стенки bc, так как поверхности АВ и ВС находятся под разным гидростатическим давлением и рассчитываются отдельно.

Пример 1.3.2. Построить эпюру вертикальной составляющей R_Y силы избыточного давления на цилиндрическую стенку.

Решение. Вертикальная составляющая выражается весом жидкости G в теле давления объемом V:

F_Y = G = r g V

Объем жидкого тела давления определяется V = S ^. В,

где S ^– поперечное сечение тела давления; В – ширина стенки.

Для построения поперечного сечения тела давления необходимо восстановить перпендикуляры из крайних точек А и В криволинейной поверхности до пересечения со свободной поверхностью жидкости. Вертикаль из точки А в данном случае восстанавливать не требуется, так как точка А уже находится на линии свободной поверхности. Фигура, отсеченная линией поверхности (в данном случае полуокружностью) и вертикалью из точки В представляет собой поперечное сечение тела давления. Сечение тела давления для данного примера выражено половиной площади круга (заштриховано). Так как тело давления получилось с не смоченной стороны (отрицательное тело давления), то направление действия F_Y противоположно действию силы тяжести G этого жидкого тела.

Примечание: В случае, когда жидкость оказывает давление изнутри, сечение тела давления будет аналогичным, но направления действия вертикальной составляющей силы давления F_Y и силы тяжести G будут совпадать, так как эпюра оказывается со смоченной стороны поверхности (положительное тело давления).

Пример 1.3.3. Металлическая цистерна диаметром D=2 м и длиной L=10м заполнена минеральным маслом с плотностью r = 0,9^.10³ кг/м³, давление на поверхности масла равно атмосферному. Определить силу давления масла на внутреннюю поверхность и точку приложения равнодействующей силы давления.

Решение: Левая и правая поверхности с образующей в виде полуокружности находятся под одинаковым давлением. Для расчета выбираем любую из них.

Равнодействующая сила давления на левую или правую поверхность определяется по формуле (1.3.1):

Горизонтальная составляющая силы давления F_Х равна силе давления на вертикальную проекцию поверхности площадью S = D L:

F_Х=r g h_c S= r g 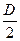D L= 0,9 ^. 10^{3 .} 9,81 ^. 2 ^. 10 = 176,6 ^.10³ Н

Вертикальная составляющая равна весу тела давления:

Равнодействующая сила:

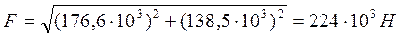
Направление действия силы определим по кoсинусу угла наклона a:

, a = 38°

Точку приложения силы F находим графическим построением. Построение в выбранном масштабе удобнее вести непосредственно от точки пересечения направлений действияF_X и F_Y.

Продолжим линии направления действия сил F_X и F_Y до их пересечения. Вектор равнодействующей силы под углом a проводим через полученную точку пересечения. В свою очередь точка пересечения образующей и направления действия равнодействующей определяет центр давления (т.D).

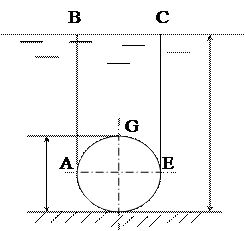Пример 1.3.4. Определить силу давления воды на трубу диаметром D = 800 мм, уложенную по дну реки на глубине h = 30 м.

Решение. Определим силу давления на 1 м длины трубы.

Горизонтальные составляющие силы давления слева и справа равны и определяются силой давления на вертикальную стенку площадью S = D ^. 1м:

F_X = r g h_C S = r g (H – D/2) D = 1000 ^. 9,81 (30 – 0,8/2) 0,8 = 232 КН

Сила, действующая на 1 м трубы сверху, определяется вертикальной составляющей силы давления и равна весу жидкого тела ABCEG объемом V_ТД:

F_Y = r g V_ТД = r g (S_ABCE - S_AGE) ^.1 =

=

Равнодействующая сила:

ТЕМА 1.4. РАВНОВЕСИЕ ТЕЛ, ПОГРУЖЕННЫХ В ЖИДКОСТЬ.

 

На поверхность частично или полностью погруженного в жидкость тела действует выталкивающая сила (архимедова сила) F_V равная по величине и противоположная по направлению весу вытесненной телом жидкости:

F_V = r g V (1.4.1)

где r - плотность жидкости, кг/м³;

V – объем жидкости, вытесненной телом, м³.

Точка приложения выталкивающей силы (центр водоизмещения) совпадает с центром тяжести вытесненного объема жидкости.

Равновесие тела имеет место при равенстве сил, удерживающих и выталкивающих тело:

F_V = F_УД (1.4.2)

Устойчивость тел от всплывания характеризуется коэффициентом всплывания

К_{ВСПЛ =} F_УД / F_V (1.4.3)

Способность плавающего тела возвращаться в состояние равновесия после отклонения из положения равновесия определяется взаимным расположением его центра тяжести (т.С) и метацентра (т.М). Метацентр – точка пересечения оси плавания тела (ав) и направления действия выталкивающей силы при отклонении (из т. D₁).

При крене центр водоизмещения D смещается (D₁).

1) Все точки на оси (ав) - состояние равновесия

2) Т.С ниже т.М - устойчивое состояние (1.4.4)

3) Т.С выше т.М – неустойчивое состояние.

Для погруженных тел (Pv = G) также различают три случая:

1) т.D выше т.С –устойчивое равновесие

2) т.D ниже т.С – неустойчивое равновесие (1.4.5)

3) т.D совпадает с т.С – безразличное равновесие.

УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ

Решение задач данной темы сводится к нахождению и сопоставлению сил, выталкивающих и удерживающих тело. При действии сил через рычаги необходимо составить уравнение моментов действующих сил.

ПРИМЕРЫ

Пример 1.4.1. Определить вес груза G, которым необходимо утяжелить пустой трубопровод диаметром D = 500мм для предотвращения его всплывания в воде. Собственный вес одного метра трубы G_ТР = 180 кг.

Решение. Трубопровод удерживается от всплывания собственным весом и весом груза (балласта). Составим уравнение равновесия сил, выталкивающих и удерживающих трубопровод:

F_V = G + G_ТР, откуда G = F_V - G_ТР

Выталкивающая сила по закону Архимеда равна силе тяжести воды, вытесненной трубопроводом.

Для одного метра трубы (L=1м) выталкивающая сила равна:

F_V = r g V = r g S_D L = r g L p D² / 4 =

=1000 ^. 9,81 ^. 1 ^. 3,14 ^. 0,8² / 4 = 4928 Н

Находим вес груза:

G = 4928 / 9,81 – 180 = 322 кг.

Пример 1.4.2. В поплавковую камеру бензин подводится по трубе d = 4 мм под давлением Р =0,3 ати. Постоянный уровень в камереШаровой поплавок и клапан укреплены на рычаге, который вращается вокруг оси 0. Определить радиус поплавка R из условия, что клапан открывает отверстие, когда поплавок погружен наполовину. Вес поплавка G_П = 25 г, вес клапана G_И = 12г, а = 40 мм, в = 15 мм, r = 700 кг/м³. Весом рычага пренебречь.

Решение. Переводим единицы измерения в систему СИ:

G_П = 25 г = 25 ^. 10^{-3 .} 9,81 = 245 ^. 10^-3 Н;

G_И = 12 г = 12 ^. 10^{-3 .} 9,81 = 118 ^. 10^-3 Н;

а = 40 мм = 40 ^. 10^-3 м; в = 15 мм = 15 ^. 10^-3 м; d = 4 мм = 4 ^. 10^-3 м;

Р = 0,3 ати = 101325 ^. 0,3 = 30398 Па.

Открывание и закрывание клапана происходит при погружении или подъеме поплавка. На поплавок действуют силы: выталкивающие – архимедова сила Р_V и вес клапана G_И; удерживающие – сила давления бензина и вес поплавка G_П. Так как силы действуют через рычаги, то уравнение равновесия составим для моментов выталкивающих и удерживающих сил относительно оси 0 в момент открытия поплавка:

Р_V ^. а + G_И ^. в = Р ^. S_d ^. в + G_П ^. а или (Р_V – G_П) а = (Р S_d – G_И) в

Архимедова сила равна весу вытесненного поплавком бензина:

Сила давления бензина на клапан определяется:

Тогда ( – G_П) а = ( – G_И) в

Решая равенство относительно R, получим:

= G_П +

Примечание: из уравнения моментов можно выразить любой входящий в уравнение параметр. Задача является типичной для емкостей различного назначения с поплавковым регулированием подачи жидкости.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: