Гидравлические сопротивления.

При движении реальной жидкости на участке между двумя сечениями часть удельной энергии (напора) потока затрачивается на преодоление сопротивлений движению жидкости. Сопротивление оказывается силами поверхностного трения за счет шероховатости стенок, ограничивающих поток, и силами внутреннего трения, обусловленного вязкостью жидкости.

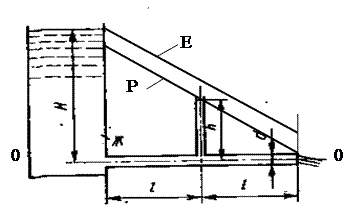
При установившемся движении реальной жидкости уравнение Бернулли имеет вид:

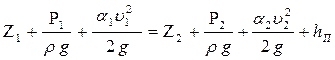(2.3.1)

или

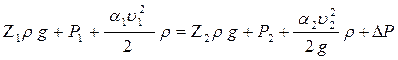(2.3.2)

где h_П – полные потери напора, м; DР – полные потери давления, Па.

a - коэффициент Кориолиса, учитывающий неравномерность распределения скоростей по сечению потока. При турбулентном режиме движения a = 1,1, при ламинарном режиме a = 2.

Полная удельная энергия потока и полный напор для двух сечений:

Е₁ = Е₂ + DР и Н₁ = Н₂ + h_П (2.3.3)

Так как все члены уравнения имеют размерность длины, то оно может быть выражено графически. Если в каждом сечении по течению потока откладывать от плоскости сравнения вверх последовательно величины Z, P/ rg и au²/2g, то можно получить напорную линию Е, которая показывает изменение полной удельной энергии потока от сечения к сечению. Линия, соединяющая точки, лежащие на высоте Z + P/rg называется пьезометрической линией Р и показывает изменение потенциальной энергии вдоль потока.

По превышению этих линий от условной плоскости сравнения можно определить полный, пьезометрический и потенциальный напор в любом сечении данного потока.

В вязкой жидкости полная удельная энергия по течению постоянно уменьшается из-за потерь на преодоление сопротивлений (напорная линия постоянно понижается). Потенциальная энергия может как увеличиваться, так и понижаться в зависимости от изменения кинетической энергии (при изменении сечения потока).

Полные потери напора складываются из линейных потерь h_i (по длине) и местных потерь h_м в местах резкого изменения конфигурации потока (в местах установки фасонных частей, диафрагм, запорно - регулирующих устройств, сужений, расширений, ответвлений, поворотов потока).

Потери напора по длине трубопровода при установившемся движении определяются по формуле Дарси –Вейсбаха:

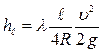, м или 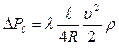, Па (2.3.4)

где l - безразмерный коэффициент гидравлического трения (коэффициент Дарси); i - длина участка, м; 4R - эквивалентный диаметр, равный для круглого сечения внутреннему диаметру трубы, м; u - средняя скорость движения, м/с.

В общем случае коэффициент гидравлического трения l зависит от вязких свойств жидкости, учитываемых числом (критерием) Рейнольдса (Re = u d / n) и от шероховатости трубы D (высоты выступов): l = f (Re, D). В технических расчетах в качестве D принимают эквивалентную шероховатость к_Э, которая представляет собой диаметр песчинок, создающих при моделировании движения в трубопроводе шероховатость, эквивалентную фактической. Принимается по справочным данным.

При разных режимах движения влияние этих факторов неодинаково.

При ламинарном режиме коэффициент l зависит только от числа Рейнольдса:

l = А / Re (2.3.5)

где А – опытный коэффициент, принимаемый по справочным данным.

Для круглых труб: l = 64 / Re.

Для квадратных труб: l = 57 / Re; (2.3.6)

Для зазора толщиной d между двумя стенками: l = 96 / Re.

При турбулентном режиме коэффициент зависит от зоны сопротивления:

В зоне гидравлически гладких труб (толщина пристенного ламинарного слоя больше выступов шероховатости) сопротивление движению зависит только от числа Рейнольдса и определяется по эмпирической формуле Блазиуса:

l = 0,3164 / Re ^0,25 (2.3.7)

В переходной (доквадратичной) зоне коэффициент трения зависит от обеих характеристик и определяется по формуле Альтшуля:

l = 0,11 (D / d + 68 / Re) ^0,25 (2.3.8.)

Эта формула справедлива для любой зоны турбулентного режима.

В зоне гидравлически шероховатых труб ламинарный подслой отсутствует, основное сопротивление определяется шероховатостью стенок. В этом случае коэффициент l определяется по формуле Шифринсона:

l = 0,11 (D / d) ^0,25 (2.3.9)

где d – диаметр трубы. Отношение D / d - относительная шероховатость.

Выбор формул для определения коэффициента гидравлического трения осуществляется по граничным числам Рейнольдса с учетом относительной шероховатости (см. график 1). Практически коэффициент определяется по графикам, составленным на основе формул (2.3.5-2.3.9), которые приводятся в справочной литературе.

 

График 1. ГРАНИЦЫ ПРИМЕНЕНИЯ ФОРМУЛ

для определения коэффициента гидравлического трения

Пуазейля Блазиуса Альтшуля Шифринсона

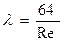
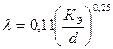
зона переходная зона

ламин. гл. зона шероховатых

область труб труб

 

 

Re

2300 2^.10⁴ 4^.10⁴ 2^.10⁶

При ламинарном режиме движения для определения линейных потерь в трубах круглого сечения обычно используется формула Пуазейля, полученная на основе формулы Дарси – Вейсбаха:

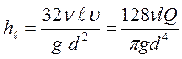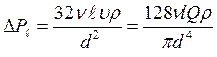или (2.3.10)

Потери напора в местном сопротивлении определяются по формуле Вейсбаха: h_м = z u² / 2g (2.3.11)

где z - коэффициент местного сопротивления, зависящий от размеров и формы сопротивления. Коэффициенты местных сопротивлений определяются опытным путем и приводятся в справочной литературе.

При ламинарном режиме движения коэффициент определяется:

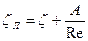(2.3.12)

где z, А – справочные коэффициенты.

При внезапном расширении или сужении потока потери можно определить по формулам:

1. При внезапном расширении потока от сечения w₁ до сечения w₂ (потери на удар):

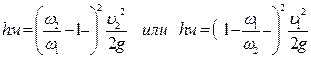, (2.3.13)

где индекс 1 относится к узкому сечению, индекс 2 – к широкому сечению.

2. При внезапном сужении происходит сжатие струи сечением w₁ до сечения w_с. Отношение сжатого сечения к узкому сечению w₂ : 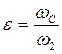- коэффициент сжатия. Принимается по справочным таблицам в зависимости от отношения w₂/w₁ или рассчитывается по эмпирической формуле:

, где n = - степень сжатия. (2.3.14)

Потери напора определяются:

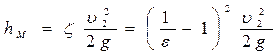(2.3.15)

Коэффициент местного сопротивления при внезапном сужении можно

определить также по формуле Идельчика:

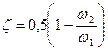(2.3.16)

3. Диафрагма.

Коэффициент местного сопротивления:

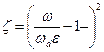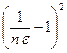= , (2.3.17)

где e = w_с /w_d; n = w_d / w; w_d – сечение диафрагмы; w - сечение трубы.

Общие потери напора на участке трубопровода определяются путем арифметического суммирования потерь по длине и местных потерь:

h_п = h_l+ åh_м - метод наложения потерь, т.е:

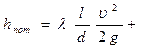
, (2.3.18)

где z_l - линейный коэффициент сопротивления (линейные сопротивления, условно замененные одним местным сопротивлением); z_с – коэффициент сопротивления трубопровода (системы).

 

УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ.

 

Уравнение Бернулли для реальной жидкости необходимо применять в случаях, когда потерями энергии пренебречь нельзя. Подход к решению задач принципиально не отличается от рассмотренного в теме 2 данного раздела, т.е. необходимо выбрать характерные сечения и записать для них уравнение Бернулли для реальной жидкости сначала в общем виде, а затем применительно к конкретным условиям задачи. Для турбулентного режима коэффициент a принимается равным 1.

В общем случае, когда сечения имеют разные превышения над плоскостью сравнения и состоят из труб разного диаметра, полные потери представляют собой разность гидродинамических напоров (полных напоров) в выбранных сечениях:

 

В частном случае, если система состоит из горизонтальной трубы постоянного сечения, то вследствие равенства превышений (Z₁=Z₂) и скоростных напоров (u₁²/2g) = (u₂²/2g) потери определяются только разностью пьезометрических напоров, т.е. показаний пьезометров:

(Р₁ /rg) - (Р₂ /rg) = h_П

После подстановки в правую часть развернутых выражений для определения полных потерь h_П по приведенным в данной теме формулам, представляется возможным из полученного уравнения выразить искомый параметр. При необходимости (получено одно уравнение с двумя неизвестными) в качестве второго уравнения используется уравнение постоянства расхода.

Для выбора расчетного выражения при определении линейных и местных потерь необходимо предварительно выяснить режим движения (определить число Рейнольдса Re). Если предварительное определение невозможно, то режимом движения необходимо задаться и, после нахождения требуемых параметров, убедиться в правильности предположения. При необходимости, выполнить перерасчет. При определении местных потерь в формулы (2.3.13,2.3.15) подставляется значение скорости для того сечения, к которому относится коэффициент местного сопротивления.

ПРИМЕРЫ

Пример 2.3.1. При истечении жидкости из резервуара в атмосферу по горизонтальной трубе диаметром d = 50мм и длиной l = 6,7м уровень в пьезометре, установленном посередине длины трубы равен h = 4 м. Определить расход Q и коэффициент гидравлического трения l, если напор в баке постоянен и равен Н = 9 м. Построить пьезометрическую и напорную линии. Сопротивлением входа в трубу пренебречь.

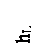
Решение.

Расход определяется: Q = v u.

Так как место установки пьезометра не позволяет учесть линейные потери концевой части трубопровода, то для нахождения скорости необходимо составить 2 уравнения Бернулли относительно плоскости 0-0, проходящей по оси трубы. Характерные сечения: свободная поверхность в баке, место установки пьезометра, конечное сечение.

Для сечений 1-1 и 2-2 после преобразований аналогично примеру 2.2.1

уравнение Бернулли принимает вид: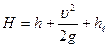

или, с учетом формулы (2.3.4) для определения линейных потерь:

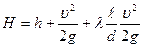(1)

Аналогично, для сечений 2-2 и 3-3:

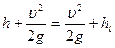или (2).

С учетом уравнения (2) после замены на h последней составляющей уравнение (1) примет вид:

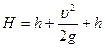, откуда 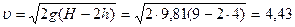м/с.

Расход по трубопроводу составляет:

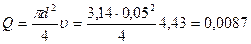м³/с = 8,7 л/с.

Из уравнения для сечений 2-2 и 3-3 находим коэффициент гидравлического трения:

Построение линии полной энергии Е:

Полная энергия (напор) в сечении 1-1 равна Н, м;

Полная энергия в сечении 2-2 равна , м;

Полная энергия в сечении 3-3 равна , м.

Падение (уклон) линии Е определяется значением удельной потери напора на преодоление линейных сопротивлений: 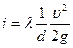- потери на 1 м длины трубы.

Расстояние по вертикали между линией полного напора Е и линией пьезометрического напора Р соответствует скоростному напору (в данном трубопроводе u²/2g = 1 м). Так как сечение трубы постоянно, то скорость и скоростной напор вдоль трубопровода не изменяется и линия Р параллельна линии Е.

Отложив вниз по вертикали от линии Е высоту, соответствующую скоростному напору u²/2g =1 м, получим линию пьезометрического давления Р, проходящую по уровню в пьезометре и через ось трубы в конечном сечении.

Пример 2.3.2. При ламинарном режиме движения жидкости по горизонтальному трубопроводу диаметром d = 30 см расход равнялся Q = 0, 424 м³/с, а падение пьезометрической высоты на участке длиной l = 230 смсоставляло h = 50 cм. Определить кинематический (n) коэффициент вязкости перекачиваемой жидкости.

Решение.

При ламинарном режиме движения линейные потери напора определяются по формуле Пуазейля (2.3.8):

Определяем скорость движения жидкости:

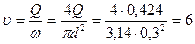м/с

Из формулы Пуазейля определяем кинематический коэффициент вязкости:

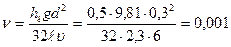м²/с = 1^.10^-3 м²/с.

Пример 2.3.3. На стыке труб с водой d₁ = 0,075 м и d₂ = 0,1 м установлена диафрагма d = 0,05м. Показание ртутного манометра h = 0,349 мм. Расход Q = 0,014 м³/с. Не учитывая потери на вход в диафрагму, определить коэффициент сжатия струи e.

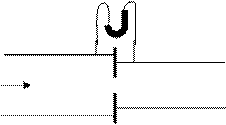Решение.

Коэффициент сжатия струи e можно определить из выражения (2.3.17) для определения коэффициента местного сопротивления диафрагмы:

=

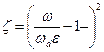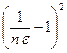
Для нахождения коэффициента e применим уравнение Бернулли, составленное для 2-х сечений в местах подключения ртутного дифференциального манометра (перед диафрагмой и за диафрагмой). Плоскость сравнения принимаем по оси труб.

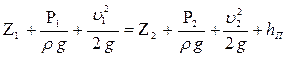, где h_П - потери в диафрагме

Для данной задачи: Z₁ = Z₂ = 0;

Разность давлений в пересчете на водяной столб: .

Потери напора в диафрагме по (2.3.11): .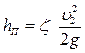

После перегруппировки и замены уравнение Бернулли для данной задачи примет вид:

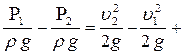
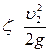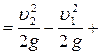
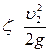или (1)

Находим скорости движения в трубах:

;

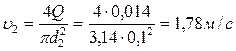
Из (1) находим коэффициент сопротивления диафрагмы:

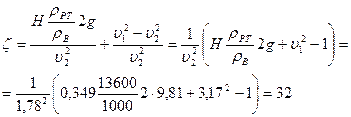
Из (2.3.17) определяем коэффициент сжатия струи:

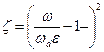= или 32 = 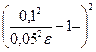, откуда

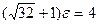и e = 0,60.

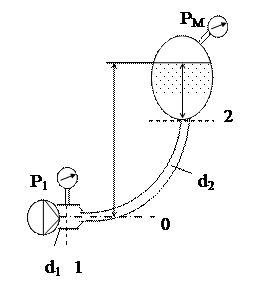
Пример 2.3.4 Насос нагнетает жидкость в напорный бак, где установились постоянный уровень на высоте Н = 2 м и постоянное давление Р_М = 0,2 МПа. Манометр, установленный на выходе из насоса на трубе диаметром d₁ =75 мм, показывает Р₁ = 0,25 МПа. Определить расход Q, если диаметр искривленной трубы, подводящей жидкость к баку d₂ = 50 мм. Эквивалентный линейный коэффициент сопротивления этой трубы принят равным z_ТР= 0,5. Плотность жидкости r = 800 кг/ м³.

Решение.

Расход определяется живым сечением и скоростью в трубе d₂: Q = w₂ u₂ .

Так как сечение w₂ задано диаметром трубы, то задача сводится к определению скорости движения. Для ее нахождения воспользуемся уравнением Бернулли. Характерным сечением для данной системы является сечение 1 в месте установки манометра после насоса. В качестве второго сечения необходимо выбрать сечение, в котором фигурирует искомая скорость движения, определяющая потери напора. В данной задаче это любое сечение по трубе d₂ (сечение 2).

Для исключения одной из геометрических высот плоскость сравнения (0-0) выберем по нижнему сечению (по оси насоса и трубы d₁).

Записываем уравнение Бернулли (2.3.1) для сечений 1 и 2 относительно оси 0-0 в общем виде:

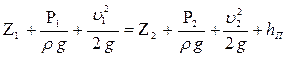
Для данной задачи: Z₁ = 0;

Обозначим высоту жидкости от свободной поверхности до второго сечения h, тогда Z₂ = H – h.

Избыточное давление в сечении 1 измеряется манометром Р₁.

Избыточное давление в сечении 2 складывается из давления Р_М и давления столба жидкости высотой h: Р₂ = Р_М + rgh.

Потери напора складываются из потерь на внезапное расширение, потерь в трубе и потерь на внезапное расширение в баке:

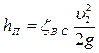
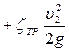
Уравнение Бернулли для данной задачи примет вид:

или

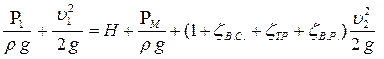
Так как скорости неизвестны для обоих сечений, то из уравнения постоянства расхода выразим скорость движения в трубе после насоса u₁, через скорость движения u₂:

w₁ u₁ = w₂ u₂, откуда u_{1 =} w₂ u₂ /w₁ = d₂² u₂ / d₁² = 0,05² u₂ / 0,075² = 0,44 u₂.

После подстановки в уравнение и перегруппировки получим:

По формуле (2.3.16) находим коэффициент местного сопротивления при внезапном сужении: z_В.С. = 0,5 (1 – d₂²/d₁²) = 0,5 (1-0,44) = 0,28.

Рассматривая сечение бака по сравнению с сечением трубы как несравнимо большое, по формуле (2.3.13) находим коэффициент местного сопротивления при внезапном расширении:

= =1

Находим скорость движения в трубе d₂:

, откуда .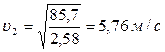

Находим расход: Q =w₂ u₂ =3,14 ^. 0,05^{2 .}5,76 / 4 = 11,3 л/с.

 

ТЕМА 2.4. ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ ОТВЕРСТИЙ И НАСАДКОВ.

 

При истечении жидкости различают:

1) малые и большие отверстия. Отверстие считают малым, если его размер составляет не более 0,1 от напора Н: d < 0,1 Н.

2) тонкие и толстые стенки. Тонкой считают стенку, если диаметр отверстия больше толщины стенки (d > d). При истечении через отверстие в толстой стенке кроме местных потерь сказываются и линейные потери.

3) полное и неполное сжатие струи. Сжатие является неполным, если отверстие расположено у дна или стенки сосуда.

4) полное сжатие может быть совершенное, когда отверстие находится от дна и стенок на расстоянии не менее 3d и несовершенное.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: