 |
Алгоритмы нахождения НОД и мультипликативного обратного по модулю.
|
|
|
|
Алгоритм Евклида.
Алгоритм А. (Алгоритм Евклида в современной редакции). По данным неотрицательным целым числам u и v этот алгоритм находит их наибольший общий делитель.
A1. [ v = 0?] Если v = 0, то выполнение алгоритма заканчивается, а в качестве результата возвращается число u.
A2. [Взять u mod v. ] Присвоить r u mod v, u v, v r и вернуться к шагу A1. (В результате выполняемых на этом шаге операций значение v уменьшается, значение НОД(u, v) остается неизменным.)
Бинарный алгоритм НОД.
Алгоритм B. (Бинарный алгоритм нахождения наибольшего общего делителя). По данным неотрицательным целым числам u и v этот алгоритм находит их наибольший общий делитель. (Использует знаковое представление чисел).
B1. [Найти степень 2.] Присвоить k 0, затем повторно присваивать kk + 1, u u / 2, v v / 2 нуль или более раз до тех пор, пока одно или оба числа u и v станут нечетными.
B2. [Начальная установка.] (Исходные значения чисел u и v уже разделены на 2 k, и по крайней мере одно из текущих значений нечетно.) Если нечетно u, то присвоить t - v и перейти к шагу B4. В противном случае присвоить tu.
B3. [Уменьшить t наполовину.] (Здесь t четно и не нуль.) Присвоить tt / 2.
B4. [ t четно?] Если t четно, то вернуться к шагу B3.
В5. [Установить max(u, v) заново.] Если t > 0, то присвоить u t, в противном случае присвоить v - t. (Большее из чисел u и v заменяется на | t | за исключением, возможно, первого выполнения этого шага.)
B6. [Вычесть.] Присвоить t u – v. Если t ¹ 0, то вернуться к шагу B3. В противном случае алгоритм останавливает выполнение, а на выходе будет u · 2 k.
Рис.33. Бинарный алгоритм НОД.
Расширенный алгоритм Евклида.
Алгоритм X. (Обобщенный алгоритм Евклида). Для заданных целых чисел u и v этот алгоритм определяет вектор (u 1, u 2, u 3), такой, что uu 1 + vu 2 = u 3 = НОД(u, v). В процессе вычисления используются вспомогательные векторы (v 1, v 2, v 3), (t 1, t 2, t 3); действия производятся таким образом, что в течение всего процесса вычисления выполняются соотношения
|
|
|
ut 1 + vt 2 = t 3 uu 1 + vu 2 = u 3 uv 1 + vv 2 = v 3.
X1. [Начальная установка.] Присвоить (u 1, u 2, u 3) (1, 0, u), (v 1, v 2, v 3) (0, 1, v).
X2. [v3 = 0?] Если v3 = 0, то выполнение алгоритма заканчивается.
X3. [Разделить и вычесть.] Присвоить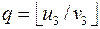 
, затем присвоить
(t 1, t 2, t 3) (u 1, u 2, u 3) – (v 1, v 2, v 3) · q,
(u 1, u 2, u 3) (v 1, v 2, v 3),
(v 1, v 2, v 3) (t 1, t 2, t 3).
Возвратиться к шагу X2.
Расширенный бинарный алгоритм НОД.
Алгоритм Y. Модификация алгоритма X с использованием принципов алгоритма B. Для заданных целых чисел u и v этот алгоритм определяет вектор (u 1, u 2, u 3), такой, что uu 1 + vu 2 = u 3 = НОД(u, v). В процессе вычисления используются вспомогательные векторы (v 1, v 2, v 3), (t 1, t 2, t 3); в течение всего процесса вычисления так же, как и в X выполняются соотношения
ut 1 + vt 2 = t 3 uu 1 + vu 2 = u 3 uv 1 + vv 2 = v 3.
(Использует знаковое представление чисел).
Y1. [Найти степень 2.] То же, что в шаге B1.
Y2. [Начальная установка.] Присвоить (u 1, u 2, u 3) (1, 0, u), (v 1, v 2, v 3) (v, 1 – u, v). Если число u нечетно, присвоить (t 1, t 2, t 3) (0, –1, – v) и прейти к шагу Y4. В противном случае присвоить (t 1, t 2, t 3) (1, 0, u).
Y3. [Выполнить половинное деление t 3.] Если t 1 и t 2 четны, присвоить (t 1, t 2, t 3) (t 1, t 2, t 3)/2; иначе присвоить (t 1, t 2, t 3) (t 1 + v, t 2 – u, t 3)/2. (В последнем случае t1 + v и t2 – u будут оба четными.)
Y4. [ t 3 четно?] Если t 3 четно, вернуться к шагу Y3.
Y5. [Переустановить max(u 3 v 3).] Если t 3 положительно, присвоить (u 1, u 2, u 3) (t 1, t 2, t 3); иначе присвоить (v 1, v 2, v 3) (v – t 1, – u – t 2, – t 3).
Y6. [Вычесть.] Присвоить (t 1, t 2, t 3) (u 1, u 2, u 3) – (v 1, v 2, v 3). Затем, если t 1 £ 0, присвоить (t 1, t 2) (t 1+ v –, t 2 – u). Если t3 ¹ 0, вернуться к шагу Y3. В противном случае закончить выполнение алгоритма с результатом, равным (u 1, u 2, u 3 · 2 k).
Китайская теорема об остатках.
Для двух cравнений.
Система cравнений
|
|
|
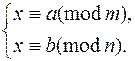
при НОД(m, n) = 1 имеет единственное решение по модулю m · n, которое определяется по формулам:
Пример.
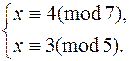
T = 7-1(mod 5) = 2-1 (mod 5) = 3 (mod 5),
u = (3 – 4) · 3 (mod 5) = 4 · 3 (mod 5) = 2 (mod 5),
x (mod 35) = 4 + 2 · 7 = 18.
Общий случай КТО.
Пусть m 1,..., mr и a 1,..., ar – целые числа, причем все mi попарно взаимно просты.
Нужно найти такой x по модулю M = m 1· m 2·...· mr, что
x = ai (mod mi) для всех i.
Решение единственно и равно:
где 
.
Пример.
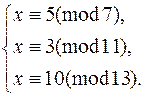
M 1 = 143, y 1 = 5,
M 2 = 91, y 2 = 4,
M 3 = 77, y 3 = 12.
|
|
|
