Кривые над полем характеристики 2

Пусть основное поле K = F _q с q = 2 ⁿ при . В этом случае j -инвариант кривой вычисляется по формуле Условие j (E) = 0, то есть a ₁ = 0, в характеристике 2 равносильно суперсингулярности кривой E, а такие кривые в криптографии не используются поэтому полагаем что j (E) ¹ 0.

В этих предположениях представитель любого класса изоморфизма эллиптических кривых над F _q записывается уравнением

E: Y ² + XY = X ³ + a ₂ X ² + a ₆,

где и 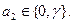Здесь γ – фиксированный элемент поля F _q, удовлетворяющий соотношению: .

Формулы группового закона: – P ₁ = (x ₁, y ₁ – x ₁) если P ₃(x ₃, y ₃) = P ₁ + P ₂ ¹ O, то

 

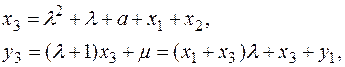
где при x ₁ ¹ x ₂

а при x ₁ = x ₂ ¹ 0

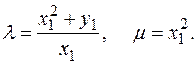
В проективных координатах формулы сложения точек эллиптической кривой, заданной уравнением

E: Y ² + XYZ = X ³ + a ₂ X ² Z ⁴ + a ₆ Z ⁶,

над полем характеристики p = 2 выглядят как

где тройка координат 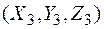вычисляется последовательно по правилу:

Координаты удвоенной точки определяются по правилу:

Сжатие точек эллиптической кривой над полем характеристики 2.

Дана точка P(x, y) на эллиптической кривой. Если y = 0, то можно положить b = 0. В противном случае вычисляют z = y / x и присваивают переменной b самый младший двоичный разряд числа z. Для восстановления y по данной паре (x, b) в случае x ¹ 0 вычисляют

и обозначают через β одно из решений уравнения z ² + z = α.

Если наименьший двоичный разряд числа β совпадает с b, то y = xβ. В противном случае y = x (β – 1).

Алгоритм цифровой подписи EC-DSA.

Алгоритм DSA можно обобщить на произвольную конечную абелеву группу A, в которой сложно решается задача дискретного логарифмирования, порождающий элемент G имеет простой порядок Q > 2¹⁶⁰ и существует открытая функция F: A ® Z / Q Z. В последнее время широкое распространение получили криптосистемы на эллиптических кривых. Аналог алгоритма DSA обобщенный для работы с эллиптическими группами точек носит название EC-DSA.

Различия в средах оперирования DSA и EC-DSA сведены в таблицу

Таблица 16. Параметры DSA и EC-DSA.

Параметр	DSA	EC-DSA
А
G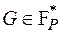
Y	Gx	[ x ] P
F	(mod Q)	x -координата по модулю Q

 

В обобщенной версии DSA каждый пользователь тоже генерирует секретный подписывающий ключ x и вычисляет открытый по формуле: Y = [ x ] P. Подпись получается в результате выполнения следующего алгоритма:

- Вычисляется хэш-значение H = H (M).

- Выбирается эфемерный ключ k, 0 < k < Q.

- Определяется R = F ([ k ] P) и S = (H + xR)/ k (mod Q).

Подписью сообщения M служит пара (R, S).

Для проверки подписи (R, S) на сообщении M осуществляют следующую процедуру:

- Вычисляют хэш-значение H = H (M).

- Определяют A = H / S (mod Q) и B = R / S (mod Q).

- Находят V = F ([ A ] P + [ B ] Y), где Y – открытый ключ подписавшего сообщение.

- Подпись считается корректной, если V = R.

Пример. Возьмем за основу эллиптическую кривую над полем F₁₉₉ вида:

E: Y ² = X ³ + X + 3.

Число ее элементов равно Q = 197, то есть является простым. Поэтому соответствующая группа – циклическая, а координаты ее образующей P – (1, 76). Выберем x = 29 в качестве закрытого ключа. Тогда соответствующий открытый ключ будет равен

Y = [ x ] P = [29](1, 76) = (113, 191).

Предположим, что владелец закрытого ключа намерен подписать сообщение с хэш-значением H (M) = 68. Тогда ему нужно сгенерировать эфемерный ключ, который выберем k = 153, и вычислить

R = x -коорд.([ k ] P) = x -коорд.([153](1, 76)) = x -коорд.((185, 35)) = 185.

Далее он находит

S = (H (M) + x · R)/ k (mod Q) = (68 + 29 · 185)/153 (mod 197) = 78.

Подпись, которую он посылает вместе с сообщением, - это пара (R, S) = (185, 78).

Чтобы проверить подпись, мы вычисляем

A = H (M)/ S (mod Q) = 68/78 (mod 197) = 112,

B = R / S (mod Q) = 185/78 (mod 197) = 15.

После этого определяем

Z = [ A ] P + [ B ] Y = [112](1, 76) + [15](113, 191) = (111, 60) + (122, 140) = (185, 35).

Подпись оказалась верной, поскольку

R = 185 = x -коорд.(Z).

 

Квантовая криптография

Идея квантовой криптографии основывается главным образом на физике фотонов. Как показано на рисунке, фотон во время своего движения производит колебания. Все четыре фотона летят в одном направлении, но в каждом случае угол колебаний различен. Угол колебаний называется поляризацией фотона, и лампочкой накаливания создаются фотоны всех поляризаций, что означает, что у части фотонов колебания будут происходить вверх-вниз, у части фотонов — влево-вправо, а у остальных колебания будут происходить при любых углах между этими направлениями. Для простоты предположим, что фотоны обладают только четырьмя возможными поляризациями, которые мы обозначим 1 2 .

Если на пути фотонов установить фильтр, называющийся поляризационным, то выходящий пучок света будет состоять из фотонов, которые колеблются в одном определенном направлении; другими словами, все фотоны будут иметь одну и ту же поляризацию. Любой фотон, поляризованный в том же направлении, что и поляризация поляризационного фильтра, заведомо пройдет через него без изменений, а фотоны, поляризованные в направлении, перпендикулярном фильтру, будут задержаны. Диагонально поляризованные фотоны, попадающие на поляризационный фильтр с вертикальной поляризацией половина из них будет задержана, а половина пройдет через фильтр, причем те, которые пройдут, приобретут вертикальную поляризацию. На верхнем рисунке показаны восемь фотонов, попадающих на поляризационный фильтр с вертикальной поляризацией, а на нижнем рисунке показано, что через фильтр благополучно прошли только четыре из восьми фотонов. Прошли все вертикально поляризованные фотоны и половина диагонально поляризованных фотонов, а все горизонтально поляризованные фотоны задержаны.

Рис.40. Прохождение поляризованных квантов через вертикальную решетку.

Именно такая способность задерживать определенные фотоны и объясняет, каким образом действуют поляроидные солнцезащитные очки.

Идея использования поляризованных фотонов для организации криптографически защищенного канала связи принадлежит американским ученым Беннету и Брассарду. Они задались вопросом, что произойдет, если зашифрованное сообщение будет представлено, а затем передано с помощью поляризованных фотонов. Сущность метода состоит в том, что противник не сможет безошибочно прочесть зашифрованное сообщение, а раз не сможет прочесть зашифрованное сообщение, то не сможет и дешифровать его.

Рассмотрим схему организации такого канала.

Допустим нам необходимо отправить зашифрованное сообщение, которое состоит из последовательности 1 и 0. Вместо этих 1 и 0 посылаются фотоны с определенными поляризациями. У нас есть две возможных схемы, с помощью которых можно связать поляризации фотонов с 1 или 0.

В первой схеме, называемой ортогональной или +-схемой, для представления 1 мы посылаем 2, а для представления 0 - 1. Во второй схеме, называемой диагональной или × -схемой, для представления 1 мы посылаем ,а для представления 0 - .

При отправке сообщения, представленного в двоичном виде, будем постоянно переключаться с одной схемы на другую непредсказуемым образом. Так что двоичное сообщение 1101101001 может быть передано следующим образом:

Сообщение
Схема	+	×	+	×	×	×	+	+	×	×
Передача

Мы передаем первую 1 с использованием +-схемы, а вторую 1 - с использованием × -схемы. Так что в обоих случаях передается 1, но всякий раз она представляется различным образом поляризованными фотонами.

Если противник захочет перехватить это сообщение, то ему потребуется определить поляризацию каждого фотона. Чтобы измерить поляризацию каждого фотона, противник должен решить, каким образом сориентировать свой поляризационный фильтр по мере прихода каждого фотона. Он не может знать наверняка, какой схемой воспользовалась мы для каждого из фотонов, поэтому наугад выбирает ориентацию поляризационного фильтра, которая окажется неверной в половине случаев. А следовательно, она не сможет точно определить содержимое передаваемого сообщения.

Для реализации симметричной схемы шифрования достаточно использовать в качестве секретного ключа последовательность поляризации (вторая строка таблицы - +×+×××++××). Но здесь мы столкнемся с проблемой распределения ключей. А при использовании короткопериодичной гаммы поляризации проявятся еще и все слабости, присущие шифрам гаммирования.

На основе этого получен вывод, что для квантовой криптографии требуется три подготовительных этапа. Хотя эти этапы не включают в себя отправку зашифрованного сообщения, с их помощью осуществляется безопасный обмен ключом, с помощью которого позднее можно будет зашифровать сообщение.

Этап 1. Абонент А начинает передавать абоненту В случайную последовательность из 1 и 0 (биты), используя для этого случайным образом выбираемые ортогональные (горизонтальная и вертикальная поляризации) и диагональные поляризационные схемы. На рисунке показана такая последовательность фотонов, движущихся к В. Таблица 17. Возможные ошибки према поляризованных квантов.

Схема А	Бит А	Фотон А	Решетка В	Ошибка	Фотон В	Бит В	Ошибка
Ортогональная			+	Нет			Нет
×	Да			Нет
		Да
		+	Нет			Нет
×	Да			Да
		Нет
Диагональная			+	Нет			Нет
		Да
×	Да			Нет
		+	Нет			Да
		Нет
×	Да			Нет

 

Этап 2. В должен измерить поляризацию этих фотонов. Поскольку он не имеет представления, какой поляризационной схемой А пользовался для каждого из фотонов, то в произвольном порядке выбирает +-решетку и ×-решетку. Иногда В выбирает правильный детектор, иногда — нет. Если В воспользуется не той решеткой, то он вполне может неправильно распознать фотон А. В таблице 17 указаны все возможные случаи.

К примеру, в верхней строке для посылки 1 абонент А использует ортогональную схему и поэтому передает 2; далее В используя правильную решетку, определяет 2 и выписывает 1 в качестве первого бита последовательности. В следующей строке действия А те же самые, но В теперь использует неверную решетку, и поэтому он может определить или , что означает, что либо он верно выпишет 1, либо неверно - 0.

Этап 3. К этому моменту А уже отправил последовательность 1 и 0, а В уже определил их; какие-то правильно, какие-то — нет. После этого А звонит В по обычной незащищенной линии и сообщает ему, какую поляризационную схему она использовала для каждого фотона, но не как он поляризовала каждый из фотонов. Так, он может сказать, что первый фотон был послан с использованием ортогональной схемы, но не скажет, какой это был фотон: 2 или 1, В сообщает А, в каких случаях он угадал с правильной поляризационной схемой. В этих случаях он, несомненно, измерил правильную поляризацию и верно выписал 1 или 0. В конечном итоге А и В игнорируют все те фотоны, для которых В пользовался неверной схемой, и используют только те из них, для которых он угадал с правильной схемой. В действительности они создали новую, более короткую последовательность битов, состоящих только из правильных измерений Боба. Весь этот этап изображен в виде таблицы в нижней части рисунка.

Благодаря этим трем этапам, абонентам А и В удалось образовать общую согласованную последовательность цифр, 11001001, которая показана на рисунке. Ключевым для этой последовательности является то, что она случайна, поскольку получена из исходной последовательности А, которая сама была случайной. Более того, события, когда В использует правильный детектор, сами являются случайными. Поэтому данная согласованная последовательность может использоваться в качестве случайного ключа. И вот теперь-то можно начать процесс зашифрования.

Рис.41. Квантовый канал обмена ключами.

Эта согласованная случайная последовательность может использоваться в качестве ключа для шифра одноразового шифрблокнота.

Во время передачи абонентом А поляризованных фотонов противник пытается измерить их, но он не знает, использовать ли +-решетку или ×-решетку. В половине случаев выбор решетки будет неверным. Это приведет к исчезновению фотонов из канала, что однозначно при виполнении этапов 2 и 3 приводит к несовпадению данных и указывает на присутствие противника в канале.

Подведем итог. Квантовая криптография является системой, которая обеспечивает секретность связи, не позволяя противнику безошибочно прочесть сообщение между абонентами. Более того, если противник попробует осуществить перехват, то абоненты смогут обнаружить его присутствие. Тем самым квантовая криптография дает абонентам возможность обменяться информацией и согласовать одноразовый шифрблокнот совершенно конфиденциальным образом, после чего они смогут использовать его в качестве ключа для зашифрования сообщения. Этот способ состоит из пяти основных этапов:

1) А посылает В последовательность фотонов, а В измеряет их.

2) А сообщает В, в каких случаях он измерил их правильно. (Хотя А и сообщает В, когда он выполнил правильное измерение, он не сообщает ему, каков должен быть правильный результат, так что, даже если противник и просматривает канал, это не представляет ровным счетом никакой опасности.)

3) Чтобы создать пару идентичных одноразовых шифрблокнотов, А и В отбрасывают те измерения, которые В выполнил неверно, и используют те из них, которые он выполнил правильно.

4) А и В проверяют неприкосновенность своих одноразовых шифрблокнотов путем сличения нескольких цифр.

5) Если процедура проверки показала удовлетворительные результаты, они могут использовать одноразовый шифрблокнот для зашифрования сообщения; если же проверка выявила ошибки, то им становится известно, что противник осуществил перехват фотонов, и им следует начать все заново.

Контрольные вопросы

1. Перечислите типы атак на симметричные криптоалгоритмы.

2. В чам разница между дифференциальным и линейным криптоанализом?

3. В чем суть атаки на основе парадокса о днях рождения?

4. Назовите отличия атаки факторизацией от атаки дискретным логарифмированием?

5. В чем заключается преимущество использования асимметричных криптосистем на основе эллиптических кривых?

6. В чем основная идея квантовой криптографии?

 

Заключение

Учебное пособие «Криптографические методы защиты информации» содержит материалы, которые следует использовать при изучении дисциплин криптографической направленности.

Изучение криптографии является одним из важнейших аспектов в специальной подготовке специалистов по защите информации. Успешное освоение данного курса позволяет изучить современные методы криптографической защиты информации. Такие знания необходимы специалисту при разработке систем защиты информации на различных уровнях обеспечения информационной безопасности личности, организации и в целом Российской Федерации. Построение систем защиты информации в современных условиях становится все более актуальным ввиду того, что уровень развития средств несанкционированного добывания информации очень высок, доступность программных средств шпионского толка превращает задачу нелегального добывания информации из уникальной и рискованной операции в достаточно простую задачу. Это значительно увеличивает риск получения больших объемов информации злоумышленниками на безопасном расстоянии от её источников путем её перехвата при обработке и хранении. Практика показывает, что эффективная защита информации с учетом этих тенденций возможна при активном использовании криптографических методов и средств защиты информации.

Содержание предлагаемого учебного пособия не претендует на обобщение всего многообразия вопросов криптографической защиты информации, но авторы надеются, что их работа будет с благодарностью оценена всеми, кому приходится сталкиваться с решением задач информационной безопасности в рамках профессиональной деятельности.

Приложение 1

⇐ Предыдущая14151617181920212223

Поделиться:

Воспользуйтесь поиском по сайту: