 |
Числовая последовательность и ее предел.
|
|
|
|
ВЫСШАЯ МАТЕМАТИКА (КРАТКИЙ КУРС ЛЕКЦИЙ)
ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
ГЛАВА 1. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ И МАТЕМАТИЧЕСКОЙ ЛОГИКИ.
Понятие множества. Некоторые сведения о математической логике.
Числовые множества. Множество действительных чисел.
Числовые промежутки.
Модуль действительного числа.
ГЛАВА 2. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ.
Понятие функции и способы ее задания.
Основные характеристики функций.
Элементарные функции.
Приложение функций в экономике.
ГЛАВА 3. ПРЕДЕЛЫ ЧИСЛОВЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И ФУНКЦИЙ
Числовая последовательность и ее предел.
Понятие предела является фундаментальным в математическом анализе. Начальные сведения о пределах встречаются еще в школьном курсе. Например, в алгебре с понятием предела связан вопрос о сумме членов бесконечной убывающей прогрессии, в геометрии – вопрос о вычислении длины окружности, площадей плоских фигур и поверхностей, объемов тел вращения.
В курсе математического анализа с помощью предела вводятся понятия производной, определенного интеграла.
Ознакомимся с понятием числовой последовательности и ее предела.
Определение. Если каждому натуральному числу n поставлено в соответствие число хn, то говорят, что задана последовательность
x1, х2, …, хn = {xn} (1.1)
Общий элемент последовательности является функцией от n.
xn = f(n)
Таким образом, последовательность может рассматриваться как функция порядкового номера элемента.
Задать последовательность можно различными способами – главное, чтобы был указан способ получения любого члена последовательности.
Примеры.
|
|
|
10) {xn} = {3n} или {xn} = 3; 6; 9; 12; …
20) {xn} = {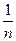 
} или {xn} = 1; 
; 
; 
; …
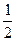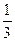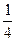30) {xn} = {(-1)n} или {xn} = -1; 1; -1; 1; …
40) {xn} = {sinpn/2} или {xn} = 1; 0; -1; 0; …
50) {xn} = {6} или {xn} = 6; 6; 6; 6; …
Для последовательностей можно определить следующие операции:
1) Умножение последовательности на число m: m{xn} = {mxn}, т.е. mx1, mx2, …
2) Сложение (вычитание) последовательностей: {xn} ± {yn} = {xn ± yn}.
3) Произведение последовательностей: {xn}×{yn} = {xn×yn}.
4) Частное последовательностей: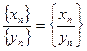 
при {yn} ¹ 0.
Замечание. Если переменная xn принимает значения x1, х2, …, хn,…, то говорят, что эта переменная «пробегает» числовую последовательность {xn}. Такую переменную называют «упорядоченной». Часто упорядоченную переменную отождествляют с числовой последовательностью, которую она «пробегает» и обозначают xn. Переменная xn не является непрерывной, она – дискретная.
Заметим, что n (номер) можно увеличивать неограниченно, пишут n→∞ и последовательность (1.1) является бесконечной числовой последовательностью.
Вернемся к рассмотренному примеру 10): {xn} = {3n} или {xn} = 3; 6; 9; 12; … На данном примере можно заметить, что при n→∞ переменная величина xn тоже неограниченно возрастает. Такие величины называют бесконечно большими.
Определение. Переменная величина xn называется бесконечно большой, если для любого (сколь угодно большого) М>0 можно найти такой номер n=N, начиная с которого все последующие значения переменной будут удовлетворять неравенству:
|xn| ³ M
Рассматривая пример 20), можно заметить, что величина xn = 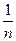→ 0 при n → ∞. Такие величины называются бесконечно малыми.
Рассмотрим еще один пример: {xn} = {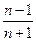 
} или {xn} = 0; ; 
; 
…
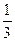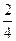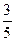По мере возрастания номера n члены числовой последовательности приближаются к числу 1. Говорят, что 1 – предел этой числовой последовательности. Точно так же в примере 20) 0 – предел этой последовательности. Кратко это записывается так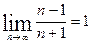 
.
Определение. Окрестностью точки а называется любой интервал (α, β), содержащий точку а. В частности, симметричный интервал (а - ε; а + ε), где ε > 0, называется ε-окрестностью точки а.
|
|
|
 |
Замечание. х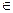 
(а - ε; а + ε)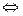 
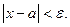
В общем случае, если последовательность {xn}имеет своим пределом число а, то это записывают так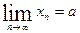 
.
Геометрически это означает, что начиная с некоторого номера n=N,N+1,N+2, … все члены последовательности попадают в ε-окрестность точки а. (ε – достаточно малое положительное число) или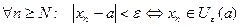 
Последовательности 30),40) не имеют предела (расходятся). Последовательность, которая имеет предел – сходится.
Определение. Число а называется пределом последовательности {xn}, если для любого положительного e>0 существует такой номер N, что для всех n > N выполняется условие:
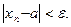
Это записывается: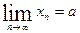
В этом случае говорят, что последовательность {xn} сходится к а при n®¥.
Свойство: Если отбросить какое-либо число членов последовательности, то получаются новые последовательности, при этом если сходится одна из них, то сходится и другая.
Пример. Доказать, что предел последовательности lim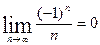 
.
Пусть при n > N верно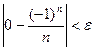 
, т.е. 
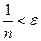. Это верно при 
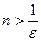, таким образом, если за N взять целую часть от 
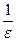, то утверждение, приведенное выше, выполняется.
Пример. Показать, что при n®¥ последовательность 3,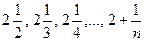 
имеет пределом число 2.
Итого: {xn}= 2 + 1/n; 1/n = xn – 2
Очевидно, что существует такое число n, что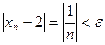 
, т.е. lim {xn} = 2.
Теорема. Последовательность не может иметь более одного предела.
Доказательство. Предположим, что последовательность {xn}имеет два предела a и b, не равные друг другу, т.е xn ® a; xn ® b; a ¹ b.
Тогда по определению существует такое число e >0, что
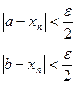
Запишем выражение: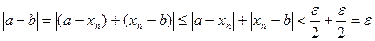 
А т.к. e- любое число, то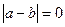 
, т.е. a = b. Теорема доказана.
Замечание. Говорят, что непрерывная переменная х → а, если эту переменную можно представить как бесконечное число числовых последовательностей, каждая из которых имеет пределом число а.
 |
Переменная х стремится к а слева (справа), если все члены последовательностей, имеющих пределом число а,
х → а -0
х → а +0
Переменная х → + ∞, если для любого сколь угодно большого М>0 найдется х, начиная с которого все следующие значения х будут больше М: х > М и х → - ∞, если для любого сколь угодно большого М>0 найдется х, начиная с которого все следующие значения х будут меньше - М: х <- М. В этих случаях переменная х называется бесконечно большой.
|
|
|
|
|
|
