 |
Индексы и индексный метод в исследовании социально-экономических явлений и процессов
|
|
|
|
Индекс (лат. index означает показатель, указатель, опись) - особый статистический относительный показатель, характеризующий соотношение во времени или пространстве различных социально-экономических явлений. С использованием индексов можно характеризовать изменение разнообразных явлений в сфере социально-экономической деятельности как на уровне микро-, так и на макро-уровне развития экономики.
Индексы, как правило, не ограничиваются простым показом отношения, а выявляют роль и значение отдельных условий и составных частей данного сложного явления. Например, индекс цен показывает, как изменились цены на все товары или отдельную группу товаров, как отразилось это изменение на соотношении количества и цен отдельных товаров, как само изменение цен отразилось на товарообороте, покупательной способности рубля, степени удовлетворения покупательского спроса. Анализируя взаимосвязи индексов можно определить, в какой мере увеличение объема продукции зависит от роста производительности труда и в какой мере от увеличения численности рабочих.
Индекс характеризует изменение величины сложного экономического явления, состоящего из элементов, которые непосредственно нельзя суммировать, поэтому он является более сложным и многосторонним показателем, чем относительные или средние величины.
Величина, изменение которой изучается в отдельном конкретном случае с помощью индекса, называется индексируемой величиной.
Для удобства в теории статистики принята следующая система обозначений:
– количество единиц данного вида продукции (товаров);
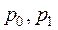– цена единицы продукции (товаров);
– себестоимость единицы продукции;
|
|
|
– затраты рабочего времени на единицу продукции (трудоемкость);
– количество продукции, выработанной в единицу времени одним работником (производительность труда);
Т 1и Т 0– затраты труда на производство продукции (Т = t ´ q).
Обозначения "0" и "1" показывают временной период. Период времени, по отношению к которому производят сравнение, называют базисным и обозначают через "0", а тот период, который сравнивают с базисным,– отчетным и обозначают его через "1". Базисный - это начальный период, т.е. период, с которым производится сравнение. Текущий (отчетный) — это период, уровень которого сравнивается.
Способ построения индексов зависит от содержания изучаемых явлений, методологии расчета исходных статистических показателей и целей исследования. Индексы можно классифицироватьпо: степени охвата элементов изучаемой совокупности; содержанию и характеру индексируемой величины; методологии их расчета.
По степени охвата элементов изучаемой совокупности различают: индивидуальные индексы и сводные (общие) индексы.
Индивидуальными индексами называются относительные числа, характеризующие соотношение отдельных величин экономических явлений: цены одного товара, себестоимости одного изделия, количества какого-либо одного реализованного продукта и т.п. Индивидуальный индекс как относительное число получается в результате сравнения двух абсолютных уровней изучаемого явления:
Индивидуальный индекс цен:
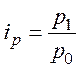
Индивидуальный индекс себестоимости:
.
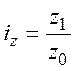Индивидуальный индекс производительности труда:
.
Индивидуальный индекс трудоемкости:
.
Например, в третьем квартале предприятие произвело 1220 штук изделия "А", а в четвертом– 1300 штук. Индивидуальный индекс физического объема продукции рассчитывается следующим образом:
.
Объем производства продукции "А" в четвертом квартале по сравнению с третьим возрос на 6,5%.
|
|
|
К индивидуальным индексам относятся показатели, публикуемые в сообщениях Государственного комитета Российской Федерации по статистике о численности населения, основных показателях денежного обращения, производства металлопродукции, объема валового накопления основного капитала и т.д. Таким образом, они характеризуют рост производства отдельных видов продукции, демографические изменения и т.д.
Сводный (общий) индекс (I) выражает соотношение уровней сложного экономического явления, состоящего из элементов непосредственно несоизмеримых. Основной формулой для расчета сводного индекса является агрегатная формула, в которой с помощью весов индекса несоизмеримые величины приводятся к сопоставимому виду.
В формуле агрегатного индекса присутствуют два элемента:
- индексируемая величина, изменение которой показывает индекс;
- некоторая постоянная величина, называемая весом или соизмерителем.
Эта форма индексов широко используется в экономико-статистических расчетах, когда возникает необходимость провести анализ изменения цен не по одному товару, а по разнообразному ассортименту товаров, изменению объема проданного количества многих различных товаров и т.п.
В зависимости от содержания и характера индексируемой величины различают: индексы количественных (объемных) показателей и индексы качественных показателей.
Необходимость построения индексов количественных показателей возникает в том случае, когда итоги по отдельным элементам сложного явления непосредственно несоизмеримы.
Например, если имеются данные о выпуске предприятием разнородной продукции в натуральном выражении, то динамику выпуска продукции в целом нельзя охарактеризовать отношением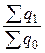 
.
Для сравнения объемов выпуска разных видов продукции в отчетном и базисном периодах необходимо привести данные к единой, общей мере (например, использовать стоимостную оценку продукции).
Тогда вместо å q получим å pq, где
p– цена единицы продукции данного вида.
Умножая цену на количество выпущенной продукции и суммируя произведения, получаем общий объем выпущенной продукции.
Выбор соизмерителя зависит от имеющейся исходной информации и от цели исследования. Универсальное значение имеют стоимостные соизмерители.
|
|
|
Например, в первом квартале производство продукции характеризуется следующими данными, приведенными в таблице 5.1.
Таблица 5.1
| Вид продукции | Количество выпущенной продукции, шт. (q) | Цена единицы продукции в базисном периоде, руб. (p 0) | |
| Базисный год | Отчетный год | ||
Агрегатный индекс физического объема продукции рассчитывается следующим образом:
,
или 119%.
Объем произведенной продукции возрос в отчетном периоде на 19%. В этом показателе индексируемой величиной является количество произведенной продукции, а весами – цены базисного периода.
Если разделить стоимость продукции отчетного периода (å p 1 q 1) на стоимость продукции базисного периода (å p 0 q 0), то получим индекс стоимости продукции:
Этот индекс характеризует изменение стоимости продукции в отчетном периоде по сравнению с базисным под влиянием двух факторов: изменения уровня цен и объема произведенной продукции.
Например, имеются следующие данные о производстве продукции:
Таблица 5.2
| Вид продукции | Произведено, штук (q) | Цена за 1 шт., тыс. руб. (p) | ||
| первое полугодие | второе полугодие | первое полугодие | второе полугодие | |
| 6,0 | 6,25 | |||
| 4,5 | 4,00 | |||
| 7,0 | 6,75 |
Рассчитаем индивидуальные и общий индексы стоимости продукции:
или 117%,
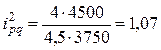
или 107%,
или 120%,
или 114%.
Общее изменение стоимости продукции в абсолютном выражении можно вычислить как разность между числителем и знаменателем индекса стоимости:
D pq = å p 1 q 1 - å p 0 q 0= 47675 - 41875 = 5800 тыс. руб.
Исходя из того, что на общее изменение стоимости продукции влияют два основных фактора: количество произведенной продукции и цена за единицу продукции, индексная модель, отражающая связь этих показателей имеет вид:
Ipq = Iq × Ip,
.
Проанализируем влияние этих факторов в абсолютном и относительном выражении:
1. Изменение стоимости продукции за счет изменения количества выпущенной продукции покажет индекс физического объема продукции
|
|
|
или 120%.
D pqq = å q 1 p 0- å q 0 p 0= 50350 - 41875 = 8475 тыс. руб.
2. Изменение стоимости продукции за счет изменения цен на произведенную продукцию покажет индекс цен:
или 95%.
D pqp = å p 1 q 1 - å p0q1 = 47675 - 50350 = –2675 тыс. руб.
Проверим взаимосвязь исчисленных показателей:
Ipq = Iq × Ip = 1,2 × 0,95 = 1,14
D pq = D qq + D pqp = 8475 - 2675 = 5800 тыс. руб.
Во втором полугодии стоимость продукции возросла на 14%, что составило 5800 тыс. руб., в том числе за счет увеличения выпуска продукции на 20% или на 8475 тыс. руб. Снижение уровня цен повлекло за собой уменьшение стоимости продукции на 5% или 2675 тыс. руб.
Взвешивание уровня себестоимости продукции по количеству продукции отчетного периода позволяет увязать индексы количественных и качественных показателей в систему. Произведение индексов физического объема продукции и себестоимости в результате даст индекс издержек производства, который характеризует изменение общего уровня затрат на производство продукции в отчетном периоде по сравнению с базисным:
Izq = Iz × Iq,
Относительная величина, характеризующая динамику среднего показателя в однородной совокупности, называется индексом переменного состава, который отражает влияние на изучаемый показатель двух факторов: изменение индексируемой величины у отдельных единиц совокупности и изменение структуры совокупности по изучаемому признаку. В связи с тем, что средние величины рассчитываются, как правило, по формуле средней арифметической взвешенной, то индекс переменного состава для любых качественных показателей может быть построен следующим образом:
,
где x – индексируемая величина, f – соизмеритель.
Индекс постоянного (фиксированного) состава характеризует динамику средних величин при одинаковой фиксированной структуре совокупности и в общем виде записывается:
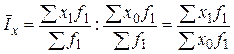
Индекс структурных сдвигов представляет собой отношение средних величин, рассчитанных при структуре совокупности отчетного и базисного периодов при постоянной величине индексируемого показателя:
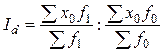
Взаимосвязь индексов переменного, постоянного состава и структурных сдвигов выражается в уравнении:
Важнейшим вопросом при построении индексов с постоянными весами является выбор базы сравнения.
В теории статистики существует несколько подходов к решению этой проблемы и соответственно несколько формул расчета индексов, названных по имени авторов. В настоящее время широко распространены индекс Пааше, Ласпейреса и Фишера.
При расчете по формуле Пааше в качестве веса берется значение соответствующей величины в текущем периоде:
|
|
|
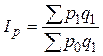
С помощью этого индекса определяется изменение цен на товары, реализованные в текущем периоде.
При расчете по формуле Ласпейреса в качестве веса используется значение соответствующей величины в базисном периоде:
Индекс характеризует изменение цен на товары, реализованные в базисном периоде.
Выбор той или иной формулы для оценки динамики качественного показателя зависит от принятой в стране методологии расчета и целей исследования.
Теоретически нет ответа на вопрос, какая из формул более точно характеризует изменение индексируемой величины.
Американский экономист И. Фишер предложил использовать среднюю геометрическую из индексов Пааше и Ласпейреса:
.
По форме построения различают сводные индексы агрегатные и средние.
Средний арифметический индекс представляет собой среднюю арифметическую из индивидуальных индексов:
Средний гармонический индекс представляет собой среднюю гармоническую из индивидуальных индексов.
При построении средних индексов: для индекса количественного показателя используют формулу среднего арифметического индекса, а для индекса качественного показателя – формулу среднего гармонического индекса.
В зависимости от выбора базы сравнения возможно построение системы цепных и базисных индексов.
Индексы с переменной базой сравнения (цепные) получают путем сопоставления индексируемого показателя каждого последующего периода с показателем предшествующего ему периода.
Индексы с постоянной базой сравнения (базисные) рассчитывают путем сравнения индексируемого показателя каждого периода с соответствующим показателем одного периода, принятого за базу сравнения.
Цепные и базисные агрегатные индексы могут быть исчислены с постоянными и переменными весами.
При изучении социально-экономических явлений в ряде случаев имеет смысл проводить анализ динамики средних показателей. Например, имеются данные о реализации продуктов на рынке за два года.
Таблица 5.3
| Продукты | Ед. изм. | Продано, тыс. ед. | Цена за единицу, руб. | ||
| 1999 г. | 2000 г. | 1999 г. | 2000 г. | ||
| Продукт 1 | л | ||||
| Продукт 2 | кг | ||||
| Продукт 3 | кг |
Необходимо рассчитать:
1) индивидуальные индексы объемов реализации в натуральном выражении, цен и выручки от реализации продуктов;
2) сводные индексы физического объема, цен по формулам Паше, Ласпейреса и Фишера;
3) сводный индекс изменения выручки от реализации продуктов в 2000 г. по сравнению с 1999 г. всего, в том числе за счет изменения объемов продажи цен.
Индивидуальные индексы объемов реализации характеризуют изменение объемов продаж в натуральном выражении по каждому виду продукции:
Продукт 1 iq1 = q1 / q0 = 1,091 (109,1%)
Продукт 2 iq2 = q1 / q0 = 0,866 (86,6%)
Продукт 3 iq3 = q1 / q0 = 1,0 (100%)
Количество проданного продукта 1 в 2000 г. увеличилось по сравнению с 1999 г. на 9,1% (109,1%- 100%), объем продажи продукта 2 сократился на 13,4% (86,6% - 100%), а объем реализации продукта 3 остался без изменения.
Индивидуальные индексы цен показывают, как изменились цены по каждому виду товара:
ip1 = p1 /p0 =1,2 (120%)
ip2 = p1 /p0 =1,333 (133,3%)
ip3 = p1 /p0 =1,166 (116,6%)
В 2000 г. по сравнению с 1999 г. цены увеличились по всем видам продукции: на продукт 1- на 20%, на продукт 2-33,3%, на продукт 3 – на 16.6%.
Индивидуальные индексы выручки отражают динамику средств, полученных от реализации отдельных видов продукции:
iw1 =q1 p1 /q0p0 =7200/5500=1,309 (130,9%)
iw2 =q1 p1 /q0p0 =10400/9000=1,156 (115,6%)
iw3 =q1 p1 /q0p0 =8750/7500=1,166 (116,6%)
В 2000 г. по сравнению с 1999 г. выручка от реализации продукта 1 выросла на 30,9%, продукта 2 – на 15,6%, продукта 3 на 16,6%.
Индивидуальные индексы выручки можно найти и через взаимосвязь индексов:
iw =iqip
Для вычисления сводных индексов заполним расчетную таблицу
Таблица 12.4
| Продукты | Выручка от реализации | |||
| 1999 г. | 2000 г. | условная | ||
| q0p0 | q1 p1 | q1 p0 | q0p1 | |
| Продукт 1 | ||||
| Продукт 2 | ||||
| Продукт 3 | ||||
| Всего |
Сводные индексы физического объема, рассчитанные по формулам Ласпейреса и Паше, составят:
I Л q =∑ q1 p0 /∑ q0p0 =21300/22000=0,968 (96,8%)
I П q =∑ q1 p1 /∑ q0p1=26350/27350=0,963 (96,3%)
Таким образом, в 2000 г. по сравнению 1999 г. в целом наблюдалось снижение объема продаж продукции в натуральном выражении на 3,2% - по формуле Ласпейреса, на 3,7% - по формуле Пааше.
Индекс Фишера:
=(0,968 0,963)0,5 =0,965 (96,5%)
Критерий Фишера дает осредненную величину снижения продажи продукции – 3,5%.
Полученные результаты по индексам физического объема можно интерпретировать и как проценты снижения выручки от реализации за счет сокращения физического объема продаж (объема продаж в натуральном выражении)
Значения сводных индексов цен:
- по формуле Ласпейреса
= 27350/22000 =1,243 (124,3%)
-по формуле Паше
=26350/21300 =1,237 (123,7%)
-по формуле Фишера
= (1,243 1,237)0,5 =1,240 (124%)
В 2000 г. по сравнению с 1999 г. наблюдался рост цен на продукцию на 24,3% по формуле Ласпейреса, на 23,7% - по формуле Паше, на 24% по формуле Фишера. Соответственно изменилась и выручка от реализации за счет роста цен.
Для расчета сводных индексов выручки от реализации используем модели, дающие одинаковый результат:
Iw = I Л q I П p =0,968 1,237=1,197 (119,7%)
Iw = I Л p I П q=0,963 1,243=1,197 (119,7%)
Выручка от реализации продукции на рынке выросла на 19,7%,
При этом абсолютное изменение выручки составит:
∆w =∑ q1 p1 -∑ q0p0 = 26350 -22000 = 4350 тыс. руб.
∆w(q) =∑ q1 p0 -∑ q0p0 = 21300 -22000 = -700 тыс. руб.
∆w(p) =∑ q1 p1 -∑ q1 p0 = 26350 – 21300 = 5050 тыс.руб.
Таким образом, выручка от реализации продуктов выросла на 4350 тыс. руб., в том числе за счет сокращения объемов продаж недополучено 700 тыс. руб., рост цен обеспечил рост выручки на 5050 тыс. руб.
Контрольные вопросы
1. Что такое ряд и уровни ряда динамики?
2. Какие отличия имеют моментный и интервальный ряды динамики?
3. Какие имеются показатели рядов динамики и их назначение?
4. В чем сущность выравнивания динамических рядов способом скользящей средней?
5. Как осуществляется параболическое выравнивание динамического ряда?
6. Суть сезонности и ее значение для экономики.
7. Что представляет собой метод простой средней, который используется для анализа сезонности?
8. Дайте определение и расчет индекса сезонности.
9. Цели и задачи прогнозирования на основе использования статистической информации.
10. Основные подходы к прогнозированию.
11. Метод прогнозирования.
12. Задачи краткосрочного прогнозирования.
13.Среднесрочное прогнозирование.
14. Задачи долгосрочного прогнозирования.
15. Основные методы экстраполяции тенденций.
16. На чем основаны поисковые прогнозы?
17. Какие задачи решаются методами статистического моделирования?
18. Каковы цели математического моделирования
19. В чем состоит задача прогнозирования на основе динамических рядов?
20. Особенности прогнозирования на основе регрессионных моделей.
21. Что такое индекс и чем он отличается от относительных и средних величин?
22. Чем характеризуется индекс?
23. Какие существуют формы индексов?
24. Что представляет собой сводная форма индексов?
25. Какая существует, взаимосвязь агрегатных индексов?
26. Охарактеризуйте гармонические индексы и расскажите, для каких целей они применяются.
27. Дайте характеристику среднеарифметического индекса.
28. В чем сущность аналитических индексов и для каких целей они применяются?
29. Индексы производительности труда и методы их расчетов.
30. Что такое индексы переменного состава и что они показывают?
31. Что такое индексы фиксированного состава и что они показывают?
32. Что представляют собой цепные и базисные индексы и для каких целей они используются?
Часть 2.
|
|
|
