 |
Характеристики асинхронного двигателя
|
|
|
|
Расчет механических характеристик
Расчет и построение естественной механической
характеристики асинхронного двигателя
Расчет естественной механической характеристики асинхронного двигателя (АД) ведется по формуле Клосса:
(1.1)
где 
- критический момент АД;
(1.2)
где 
- перегрузочная способность АД;
(1.3)
где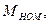 
- соответственно номинальный момент, мощность и угловая скорость АД;
(1.4)
где 
- номинальная частота вращения АД.
мин 
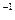
Н∙м
Н∙м
Величина критического скольжения определяется по формуле:
(1.5)
где 
- номинальное скольжение АД;
(1.6)
где 
- синхронная частота вращения АД;
(1.7)
где 
- частота переменного тока, 
Гц; 
- число пар полюсов АД
мин ;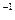
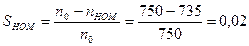
Определяют коэффициент
(1.8)
где 
- активное сопротивление фазы статора АД;
- активное сопротивление фазы ротора, приведенное к цепи статора АД.
Определяют активное сопротивление фазы статора:
(1.9)
где 
- номинальное напряжение статора АД;
- номинальный ток фазы статора АД;
Ом
Определяют активное сопротивление фазы ротора, приведенное к статору АД:
(1.10)
где 
- номинальная линейная ЭДС ротора АД;
- номинальный ток фазы ротора АД;
- коэффициент трансформации АД.
Коэффициент трансформации АД находится по формуле:
(1.11)
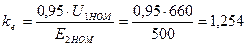
Ом
.
Задаваясь скольжением в диапазоне 
рассчитывают момент и угловую скорость АД в двигательном режиме. Результаты расчетов сводят в табл.1.1
Угловая скорость АД определяется по формуле:
;
где 
с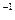
Таблица 1.1
| 
| 
| 
| 
| 
| 
|
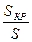
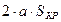
| 0,2784 |
| 78,54 | |||
| 0,23 | 4,35 | 0,2784 | 4,8584 | 2241,35 | 76,97 |
| 0,08 | 0,92 | 1,0875 | 0,2784 | 2,2859 | 4763,72 | 72,26 |
| 0,2784 | 2,2784 | 4779,4 | 71,71 | ||
| 0,12 | 1,38 | 0,725 | 0,2784 | 2,3834 | 4568,84 | 69,11 |
| 0,2 | 2,3 | 0,435 | 0,2784 | 3,0134 | 3613,65 | 62,83 |
| 0,4 | 4,6 | 0,2175 | 0,2784 | 5,0959 | 2136,89 | 47,12 |
| 0,6 | 6,9 | 0,145 | 0,2784 | 7,19 | 1514,52 | 31,42 |
| 0.8 | 9,2 | 0,10875 | 0,2784 | 9,58715 | 1135,83 | 15,71 |
| 11,5 | 0,087 | 0,2784 | 11,8654 | 917,74 |
|
|
|
Естественная механическая характеристика, построенная по данным табл.1.1, представлена на рис.1.1.
Искусственные механические характеристики АД строятся графически. Для этого задаются максимальным моментом 
и откладывают его на оси абсцисс (точка “а”). Определяют момент переключения 
(где 
- момент сопротивления, равный 
) и откладывают его также на оси абсцисс. Из точки “а” восстанавливают перпендикуляр до пересечения с прямой, проведенной из точки 
параллельно оси абсцисс. Находят точку “к”. Соединяя две точки с координатами (
), (
) прямой, получают первую искусственную механическую характеристику АД с максимальным сопротивлением пускового резистора 
.
Для построения второй искусственной характеристики поступают следующим образом. Из точки “б” пересечения перпендикуляра, соответствующего моменту 
, с первой искусственной характеристикой проводят прямую параллельную оси абсцисс до пересечения с перпендикуляром, соответствующим моменту 
, находят точку “в”. Точку с координатами () соединяют с точкой “в” прямой, которая будет являться новой искусственной характеристикой соответствующей второй пусковой ступени с сопротивлением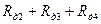 
.
Для построения третьей искусственной характеристики из точки “г” проводят прямую параллельно оси абсцисс до пересечения с перпендикуляром, восстановленным из точки “а”. Полученную точку “д” соединяют с точкой () прямой, которая и будет являться третьей искусственной характеристикой соответствующей пусковой ступени с сопротивлением 
.
Для построения четвертой искусственной характеристики из точки “е” проводят прямую параллельно оси абсцисс до пересечения с перпендикуляром, восстановленным из точки “а”. Полученную точку “ж” соединяют с точкой, координаты которой (). Получают прямую, которая будет являться четвертой пусковой ступенью с сопротивлением 
.
|
|
|
Сопротивления ступеней пусковых резисторов находят следующим образом. Из точки с координатами () проводят прямую параллельно оси абсцисс до пересечения с перпендикуляром, восстановленным из точки “а”. Получают точку “к”. Тогда отрезок “ки” будет соответствовать активному сопротивлению 
фазы ротора АД.
Отрезки на линии “ки” соответствуют величинам сопротивлений пусковых резисторов в определенном масштабе. Для определения этого масштаба находят сопротивление фазы ротора:
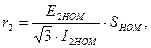
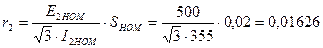Ом;
Тогда масштаб сопротивлений будет равен:
,
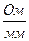
Величины сопротивлений пусковых резисторов 
разных ступеней определяются отрезками “ав”, “вд”, “дж”, “жи”:
;
Ом;
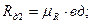
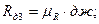
Ом;
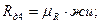
Ом;
Ом.
Таким образом, для получения первой искусственной механической характеристики АД в цепь ротора вводится пусковой резистор с сопротивлением . Вторая пусковая ступень соответствует сопротивлению 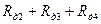, третья пусковая ступень - , четвертая - .
|
|
|
