 |
Расчет и построение механических переходных процессов
|
|
|
|
2.1 Расчет механических переходных процессов в
Двигательном режиме
Расчет переходных процессов с линейными механическими характеристиками двигателями ведется по формулам:
- для угловой скорости
 ; (2.1)
; (2.1)
- для момента
 , (2.2)
, (2.2)
где  - соответственно начальная и конечная угловые скорости двигателя;
- соответственно начальная и конечная угловые скорости двигателя;
 - соответственно начальный и конечный моменты двигателя;
- соответственно начальный и конечный моменты двигателя;
 - механическая постоянная времени электропривода.
- механическая постоянная времени электропривода.
Произведем расчет механического переходного процесса при пуске привода с линейной механической характеристикой двигателя и постоянным моментом сопротивления рабочей машины. Рассмотрим пуск двигателя в пять ступеней.
При пуске двигателя  , а
, а  - соответствующая моменту сопротивления
- соответствующая моменту сопротивления  , тогда работа двигателя на первой ступени описывается выражением:
, тогда работа двигателя на первой ступени описывается выражением:
 , (2.3)
, (2.3)
где  - конечная угловая скорость двигателя, соответствующая работе привода на первой ступени пускового резистора (т.е. для первой ступени
- конечная угловая скорость двигателя, соответствующая работе привода на первой ступени пускового резистора (т.е. для первой ступени  , соответствующая моменту сопротивления
, соответствующая моменту сопротивления  при полностью введенном сопротивлении).
при полностью введенном сопротивлении).
Тогда получим:
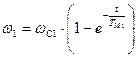 , (2.3.1)
, (2.3.1)
 - механическая постоянная времени, соответствующая работе привода на первой ступени пускового резистора:
- механическая постоянная времени, соответствующая работе привода на первой ступени пускового резистора:
- для асинхронного двигателя
 , (2.4)
, (2.4)
где  - момент инерции электропривода, приведенный к валу двигателя;
- момент инерции электропривода, приведенный к валу двигателя;
 - скольжение АД на искусственной механической характеристике, соответствующее номинальному моменту.
- скольжение АД на искусственной механической характеристике, соответствующее номинальному моменту.
Механическая постоянная времени:
- для асинхронного двигателя, работающего на естественной механической характеристике
 , (2.5)
, (2.5)
где  .
.
Тогда
 - для асинхронного двигателя, где
- для асинхронного двигателя, где  - скольжение
- скольжение
на искусственной механической характеристике при номинальном моменте.
Конечная угловая скорость на первой пусковой ступени  . Работа двигателя на первой пусковой ступени длится
. Работа двигателя на первой пусковой ступени длится  . Задаваясь временем от
. Задаваясь временем от  до
до  , определяют угловую скорость двигателя и результаты расчетов сводят в табл. 2.1.
, определяют угловую скорость двигателя и результаты расчетов сводят в табл. 2.1.
|
|
|
Расчеты:
 кг∙м2;
кг∙м2;
 с;
с;
 с;
с;
 ;
;
 с-1;
с-1;
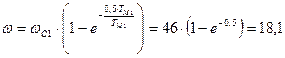 с-1;
с-1;
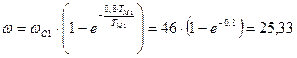 с-1;
с-1;
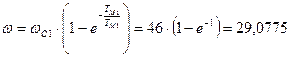 с-1;
с-1;
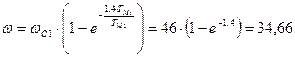 с-1;
с-1;
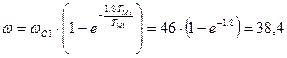 с-1;
с-1;
 с-1;
с-1;
 с-1;
с-1;
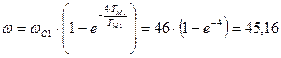 с-1.
с-1.
Таблица 2.1
 , с , с
| 0,2376 | 0,396 | 0,6336 | 0,792 | 1,1088 | 1,4256 | 1,584 | 2,376 | 3,168 | |
 , с , с 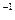
| 13,81 | 20,99 | 29,34 | 33,57 | 41,39 | 45,98 | 48,91 | 50,62 | 51,68 | |
 , Н∙м , Н∙м
| 4062,5 | 3440,4 | 3118,1 | 2740,8 | 2545,3 | 2254,2 | 2059,1 | 1987,2 | 1781,9 | 1706,4 |
По данным таблицы 2.1 строится кривая зависимость угловой скорости от времени  , которая приведена на рис 2.1. Однако, при реализации автоматического управления пуском, двигатель разгоняется лишь до скорости
, которая приведена на рис 2.1. Однако, при реализации автоматического управления пуском, двигатель разгоняется лишь до скорости  , т.к. при этой скорости происходит переход двигателя на новую механическую характеристику. Поэтому для определения времени работы двигателя на первой ступени, на оси ординат откладывают значение скорости
, т.к. при этой скорости происходит переход двигателя на новую механическую характеристику. Поэтому для определения времени работы двигателя на первой ступени, на оси ординат откладывают значение скорости  и из этой точки проводят прямую параллельную оси абсцисс до пересечения с кривой
и из этой точки проводят прямую параллельную оси абсцисс до пересечения с кривой  . Из полученной точки “а” опускают перпендикуляр на ось абсцисс и находят время работы двигателя на первой ступени пускового резистора
. Из полученной точки “а” опускают перпендикуляр на ось абсцисс и находят время работы двигателя на первой ступени пускового резистора  . Далее расчет зависимости
. Далее расчет зависимости  ведется по формуле (2.1), в которой начальными и конечными условиями будут:
ведется по формуле (2.1), в которой начальными и конечными условиями будут:  ,
,  . Механическая постоянная времени электропривода:
. Механическая постоянная времени электропривода:
- для асинхронного двигателя
 - где
- где  берется из графика (рис.1.1);
берется из графика (рис.1.1);
Аналогично предыдущему задаются временем  и рассчитывают
и рассчитывают  , а результаты расчетов сводят в табл. 2.2.
, а результаты расчетов сводят в табл. 2.2.
Расчеты:
 с
с
 ;
;
 ;
;
где 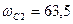 с-1, а
с-1, а  с-1 (из рис.1.1)
с-1 (из рис.1.1)
 с-1;
с-1;
 с-1;
с-1;
 с-1;
с-1;
 с-1;
с-1;
 с-1;
с-1;
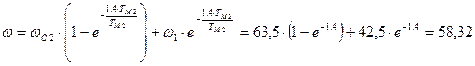 с-1;
с-1;
 с-1;
с-1;
 с-1;
с-1;
 с-1;
с-1;
 с-1.
с-1.
Таблица 2.2
 , с , с
| 0,105 | 0,175 | 0,28 | 0,35 | 0,49 | 0,63 | 0,7 | 1,05 | 1,4 | |
 , с , с 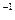
| 42,5 | 47,94 | 50,76 | 54,07 | 55,77 | 58,32 | 60,02 | 60,66 | 62,46 | 63,12 |
 , Н∙м , Н∙м
| 4062,5 | 3440,4 | 3118,1 | 2740,8 | 2545,3 | 2254,2 | 2059,1 | 1987,2 | 1781,9 | 1706,4 |
По данным табл. 2.2 построена кривая  для второй ступени пускового резистора, которая приведена на рис.2.1. Двигатель, работая на второй ступени пускового резистора
для второй ступени пускового резистора, которая приведена на рис.2.1. Двигатель, работая на второй ступени пускового резистора 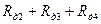 , разгоняется только до скорости
, разгоняется только до скорости  . Поэтому откладывают эту скорость на оси ординат рис. 2.1 и проводят из этой точки прямую, параллельную оси абсцисс, до пересечения с кривой
. Поэтому откладывают эту скорость на оси ординат рис. 2.1 и проводят из этой точки прямую, параллельную оси абсцисс, до пересечения с кривой  . Точку пересечения сносят на ось абсцисс и находят время
. Точку пересечения сносят на ось абсцисс и находят время  работы двигателя на второй ступени пускового резистора. И так далее до перехода на естественную характеристику, работа на которой подчиняется выражению (2.1).
работы двигателя на второй ступени пускового резистора. И так далее до перехода на естественную характеристику, работа на которой подчиняется выражению (2.1).
|
|
|
Начальными и конечными условиями для третьей ступени будут:  ,
,  . Задаваясь временем
. Задаваясь временем  от
от  до
до  , находят
, находят  , а результаты расчетов заносят в табл. 2.3.
, а результаты расчетов заносят в табл. 2.3.
Расчеты:
 с,
с,
 ;
;
 ;
;
где  с-1, а
с-1, а  с-1 (из рис.1.1)
с-1 (из рис.1.1)
 с-1;
с-1;
 с-1;
с-1;
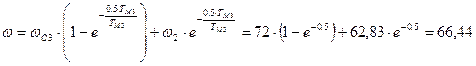 с-1;
с-1;
 с-1;
с-1;
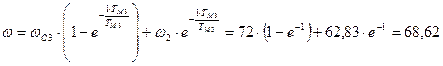 с-1;
с-1;
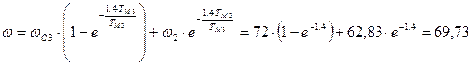 с-1;
с-1;
 с-1;
с-1;
 с-1;
с-1;
 с-1;
с-1;
 с-1.
с-1.
Таблица 2.3
 , с , с
| 0,0457 | 0,0762 | 0,1218 | 0,1523 | 0,2132 | 0,2741 | 0,3046 | 0,4569 | 0,6092 | |
 , с , с 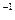
| 62,83 | 65,21 | 66,44 | 67,88 | 68,62 | 69,73 | 70,49 | 70,76 | 71,54 | 71,83 |
 , Н∙м , Н∙м
| 4062,5 | 3440,4 | 3118,1 | 2740,8 | 2545,3 | 2254,2 | 2059,1 | 1987,2 | 1781,9 | 1706,4 |
По данным табл. 2.3 построена кривая  для третьей ступени пускового резистора, которая приведена на рис.2.1. Двигатель, работая на третьей ступени пускового резистора
для третьей ступени пускового резистора, которая приведена на рис.2.1. Двигатель, работая на третьей ступени пускового резистора 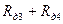 , разгоняется только до скорости
, разгоняется только до скорости 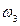 . Поэтому откладывают эту скорость на оси ординат рис. 2.1 и проводят из этой точки прямую, параллельную оси абсцисс, до пересечения с кривой
. Поэтому откладывают эту скорость на оси ординат рис. 2.1 и проводят из этой точки прямую, параллельную оси абсцисс, до пересечения с кривой  . Точку пересечения сносят на ось абсцисс и находят время
. Точку пересечения сносят на ось абсцисс и находят время 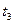 работы двигателя на третьей ступени пускового резистора. Начальными и конечными условиями для четвертой ступени будут:
работы двигателя на третьей ступени пускового резистора. Начальными и конечными условиями для четвертой ступени будут:  ,
,  . Задаваясь временем
. Задаваясь временем  от
от  до
до 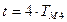 , находят
, находят  , а результаты расчетов заносят в табл. 2.4.
, а результаты расчетов заносят в табл. 2.4.
Расчеты:
 с
с
 ;
;
 ;
;
где  с-1, а
с-1, а  с-1 (из рис.1.1)
с-1 (из рис.1.1)
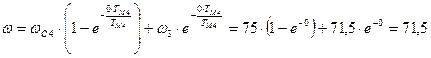 с-1;
с-1;
 с-1;
с-1;
 с-1;
с-1;
 с-1;
с-1;
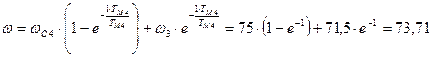 с-1;
с-1;
 с-1;
с-1;
 с-1;
с-1;
 с-1;
с-1;
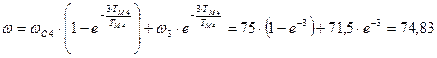 с-1;
с-1;
 с-1;
с-1;
Таблица 2.4
 , с , с
| 0,0216 | 0,036 | 0,0576 | 0,072 | 0,1008 | 0,1296 | 0,144 | 0,216 | 0,288 | |
 , с , с 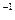
| 71,5 | 72,41 | 72,88 | 73,43 | 73,71 | 74,13 | 74,42 | 74,53 | 74,83 | 74,94 |
 , Н∙м , Н∙м
| 4062,5 | 3440,4 | 3118,1 | 2740,8 | 2545,3 | 2254,2 | 2059,1 | 1987,2 | 1781,9 | 1706,4 |
По данным табл. 2.4 построена кривая  для четвертой ступени пускового резистора, которая приведена на рис.2.1. Двигатель, работая на четвертой ступени пускового резистора
для четвертой ступени пускового резистора, которая приведена на рис.2.1. Двигатель, работая на четвертой ступени пускового резистора  , разгоняется только до скорости
, разгоняется только до скорости  . Поэтому откладывают эту скорость на оси ординат рис. 2.1 и проводят из этой точки прямую, параллельную оси абсцисс, до пересечения с кривой
. Поэтому откладывают эту скорость на оси ординат рис. 2.1 и проводят из этой точки прямую, параллельную оси абсцисс, до пересечения с кривой  . Точку пересечения сносят на ось абсцисс и находят время
. Точку пересечения сносят на ось абсцисс и находят время  работы двигателя на четвертой ступени пускового резистора. Начальными и конечными условиями, при переходе на естественную характеристику, будут:
работы двигателя на четвертой ступени пускового резистора. Начальными и конечными условиями, при переходе на естественную характеристику, будут:  ,
,  ,
,  . Задаваясь временем
. Задаваясь временем  от
от  до
до  , находят
, находят  , а результаты расчетов заносят в табл. 2.5.
, а результаты расчетов заносят в табл. 2.5.
|
|
|
Расчеты:
 с;
с;
 ;
;
 ;
;
где  с-1, а
с-1, а  с-1 (из рис.1.1)
с-1 (из рис.1.1)
 с-1;
с-1;
 с-1;
с-1;
 с-1;
с-1;
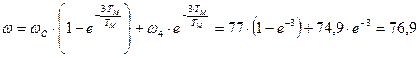 с-1.
с-1.
Таблица 2.5
 , с , с
| 0,023 | 0,046 | 0,069 | |
 , с , с 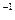
| 74,9 | 76,23 | 76,71 | 76,9 |
 , Н∙м , Н∙м
| 4062,5 | 2545,34 | 1987,22 | 1781,89 |
По данным табл. 2.5 построена следующая часть кривой  , характеризующая работу двигателя на естественной механической характеристике, которая представлена на рис.2.1
, характеризующая работу двигателя на естественной механической характеристике, которая представлена на рис.2.1
Расчет зависимости  ведут по формуле (2.2), в которой начальные и конечные значения
ведут по формуле (2.2), в которой начальные и конечные значения  ,
,  одинаковы для всех ступеней пускового резистора, а изменяется лишь величина механической постоянной времени. Для первой пусковой ступени
одинаковы для всех ступеней пускового резистора, а изменяется лишь величина механической постоянной времени. Для первой пусковой ступени  , для второй ступени
, для второй ступени  и т.д. Задаваясь временем
и т.д. Задаваясь временем  с теме же значениями, что и при расчете кривой
с теме же значениями, что и при расчете кривой  , находят момент
, находят момент  , а результаты расчетов заносят в табл. 2.1-2.5. По данным табл. 2.1-2.5 построена кривая
, а результаты расчетов заносят в табл. 2.1-2.5. По данным табл. 2.1-2.5 построена кривая  , которая представлена на рис. 2.1.
, которая представлена на рис. 2.1.
Расчеты:
 ;
;
т.к.  , а
, а  , получим:
, получим:
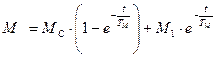 ;
;
где  Н∙м, а
Н∙м, а 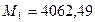 Н∙м.
Н∙м.
 Н∙м;
Н∙м;
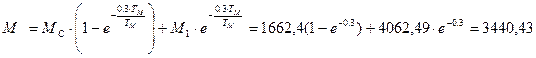 Н∙м;
Н∙м;
 Н∙м;
Н∙м;
 Н∙м;
Н∙м;
 Н∙м;
Н∙м;
 Н∙м;
Н∙м;
 Н∙м;
Н∙м;
 Н∙м;
Н∙м;
 Н∙м;
Н∙м;
 Н∙м.
Н∙м.
Заносим полученные значения для моментов в таблицы 2.1 – 2.5.
|
|
|


