 |
Домкрат и гидравлический мультипликатор
|
|
|
|
В машиностроении широко используется передача энергии и давления с помощью различных гидравлических механизмов, в которых применяются одни и те же принципы работы, основанные на практической несжимаемости жидкости (высоком модуле упругости) и преобразовании сил по закону Паскаля.
Для анализа особенностей работы домкрата рассмотрим сообщающиеся сосуды (рис. 2.10). Так как давление от приложенной внешней силы по закону Паскаля равномерно распространяется во все стороны, то под действием силы F1 жидкость вытесняется в соседний сосуд под давлением p= F1/S1 и действует на поверхность поршня площадью S2 с силой, равной F2 =F1S2/S1, при этом
F2/F1=S2/S1.
 |
 |
Так как объемы вытесняемой жидкости пропорциональны площадям и соответствующим перемещениям, то S1h1= S2h2, откуда h2 / h1= S1 / S2, т. е. перемещения поршней обратно пропорциональны их площадям.
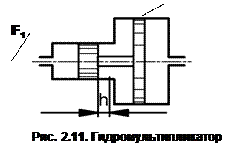
Рассмотрим случай, когда два поршня соединены друг с другом (рис. 2.11). Данный гидравлический мультипликатор применяется в ряде случаев для повышения давления в отдельных элементах гидросистемы, например в различных приспособлениях. При этом на поверхность площадью S1 действует давление P1 и возникает сила F1, которая через шток передается на поверхность площадью S1. В результате возникает давление P2= F1 / S2, т. е
P1S1 /S2=P2 или P1/P2=S2/S1.
 |
Следовательно, при передаче давлений их отношение обратно пропорционально отношению площадей поршней.
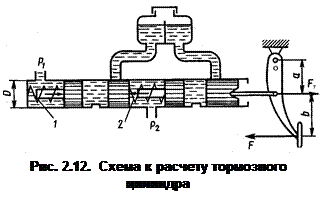
Задача. На рис. 2.12. представлена схема главного тормозного цилиндра автомобиля в момент торможения. Определить силу F, которую необходимо приложить к педали тормоза, чтобы давление в рабочих цилиндрах передних колес было p1=6 МПа. Каким при этом будет давление в рабочих цилиндрах задних колес р2? При расчете принять:
|
|
|
усилие пружины 1 F1=100 Н, пружины 2 F2= 150 Н, d =20 мм, а=60 мм, b=180 мм. Силами трения пренебречь.
Решение.
Составим уравнение равновесия для двух левых поршней с пружинами

откуда найдем р2.
Определяем усилие Ft действующую на вторую группу поршней от давления и усилия пружины

Используя уравнение моментов относительно точки О, найдем необходимое усилие F.
Задача.
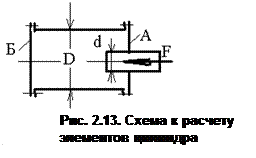 |
Определить (рис. 2.13) нагрузку на болты крышек А и Б гидравлического цилиндра диаметром D=160 мм, если к плунжеру диаметром d =120 мм приложена сила F=20 кН.
Решение.
Давление в цилиндре р=F/(pd2/4)=4*20000/(p*0.122)=1.77МПа.
Сила на крышку Б: FБ= (pD2/4)*p =(p*0.162 /4)*1770000=36кН.
Сила на крышку А: FА=(pD2/4 -pd2/4)*р =36000-20000=16кН.
Гидравлический пресс
В практике существуют гидравлические машины, действие которых основано на применении законов гидромеханики, в частности на законе Паскаля. На рис. 2.14 представлена схема простейшего гидравлического пресса. С помощью такого устройства можно получить значительный выигрыш в силе. Гидравлический пресс состоит из следующих основных частей: рычага 1, малого цилиндра 2 с поршнем диаметром d, большого цилиндра 3 с поршнем диаметром D. Прикладывая к рычагу силу Q, действуем на малый поршень силой Р1. В результате этого жидкость сжимается и давление передается на поршень большего цилиндра. Сила давления на поршень диаметром D равна Р2. Зная: соотношения длин рычагов а, в; диаметры цилиндров; коэффициент полезного действия пресса, учитывающий потери на трение (h=0,8 – 0,85) можно получить расчетную формулу гидравлического пресса в виде:
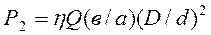 .
.
 |
Задача: Определить усилие Q, которое следует приложить к рычагу гидравлического пресса для получения усилия Р2=200кН, если известно: в=1м, а=0,1 м, D=300 мм, d=30 мм, h=0,8.
Решение.
Используя предыдущую зависимость, можно относительно силы приложенной к рычагу записать: 
|
|
|
Равновесие и остойчивость тел, погруженных в жидкость
Закон Архимеда
Рассмотрим силы давления жидкости на тело, погруженное в эту жидкость (рис. 2.15, а).
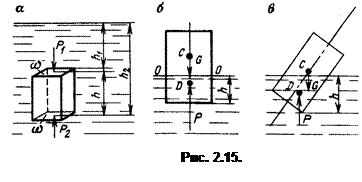 |
Тело призматической формы имеет высоту h и площадь верхнего и нижнего оснований w. Верхнее основание погружено в жидкость на глубину h1, нижнее — на глубину h2. При этом на тело действуют:
сила гидростатического давления жидкости на верхнее основание
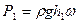
сила гидростатического давления жидкости на нижнее основание
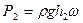
силы давления жидкости на боковые поверхности (грани призмы) не учитываются, так как они взаимно уравновешены.
Равнодействующая сил гидростатического давления равна разности сил P1 и P2 и направлена вверх (в сторону большей) силы):
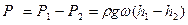 ,
,
или 
Таким образом, на тело, погруженное в жидкость, действует выталкивающая сила, равная весу жидкости, вытесненной телом. Это и есть закон Архимеда, открытый им в 250 г. до н. э.
Закон Архимеда справедлив для тел любой фирмы, так как тело другой, отличающейся от призматической и более сложной формы можно представить состоящим из бесконечного множества элементарных вертикальных призм.
|
|
|


