Закон неразрывности потока

 

Основное уравнение кинематики жидкости – уравнение неразрывности, которое вытекает из условия несжимаемости жидкости и сплошности движения.

Рассмотрим установившееся движение в русле переменного се­чения (рис. 3.3). Выберем два произвольных сечения /—/ и //—//, нормальных к оси потока, и рассмотрим участок потока, заключен­ный между сечениями.

При течении жидкости по трубопроводу переменного сечения без разрывов сплошности масса жидкости, проходящей через любое поперечное сечение канала, должна быть постоянной, т.е.

 

r₁w₁v₁= r₂S₂v₂=r_iw_iv_i=const

 

 

где v₁, v₂ — скорости жидкости в сечениях 1 и 2; w₁, w₂ - площади двух поперечных сечений трубопровода; r₁, r₂ - плотности жидкости.

Если пренебречь сжимаемостью жидкости, то ее плотность в любом сечении будет одинакова и

 

v₁w₁= w₂v₂= w_iv_i=const,

 

что выражает закон неразрывности потока.

Уравнения движения идеальной жидкости

При движении идеальной жидкости в отличие от состояния ее равновесия, равнодействующая сил, приложенных к элементарному объему, отлична от нуля и согласно принципу Даламбера равна силе инерции. Проекциями, отнесенной к массе объема жидкости силы инерции на оси х, у, z, являются

.

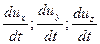Введя их в уравнения равновесия жидкости (2.2), получим систему диф­ференциальных уравнений Эйлера движения идеальной жидкости

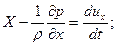
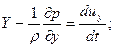
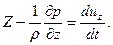
Энергия элементарной струйки

Известно, что механическая энергия любого тела характеризу­ется двумя величинами: кинетической и потенциальной энергиями. Так, если тело или частица имеет массу m и движется со скоростью v, то ее кинетическая энергия

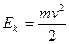
потенциальная энергия тела (частицы), поднятого на высоту

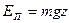
Кроме того, если масса жидкого тела занимает объем V и нахо­дится под давлением р, то это тело еще обладает потенциальной энергией давления

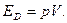
Действительно, если сосуд наполнять жидкостью под давлени­ем, то в нем будет накапливаться энергия, которая может стать до­статочной для разрушения сосуда.

На основании изложенного полная механическая энергия эле­ментарной струйки (частицы), имеющей массу m и некоторую ско­рость u, определится так:

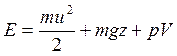Так как 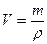, то

 

.

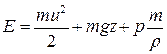Удельная энергия струйки, т. е. энергия, отнесенная к единице веса, определится делением всех членов последнего уравнения на вес элементарной струйки — mg:

.

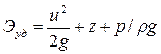2g

Энергия потока жидкости

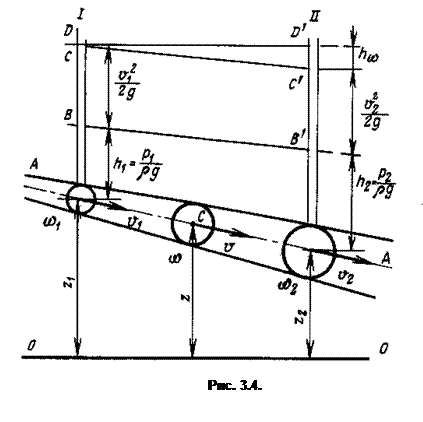
Учитывая, что поток жидкости представляет собой совокуп­ность множества элементарных струек, и принимая движение по­тока установившимся или плавно изменяющимся, можно опре­делить удельную энергию потока жидкости конечных размеров. Рассмотрим поток жидкости в виде наклонной трубы с плавно изменяющимся сечением (рис. 3.4). Внутри потока выделим неко­торую точку с. Обозначим расстояние от этой точки до произволь­но выбранной плоскости О - О (плоскость сравнения) -Z₁, давле­ние жидкости в центре тяжести сечения — р, среднюю скорость движения жидкости в выбранном сечении — v.

Полная удельная энергия потока равна сумме удельной кине­тической энергии потока Э_к и удельной потенциальной энергии Э_п,

Э_у= Э_к + Э_п,

Определим слагаемые правой части:

где п — число элементарных струек; и — скорости элементарных струек; v — средняя скорость потока; a — коэффициент, учиты­вающий неравномерность распределения скорости по сечению. 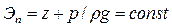, что, согласно гидростатическому закону,формулируется так:

для всех точек, данного объема покоящейся жидкости удель­ная потенциальная энергия относительно выбранной плоскости сравнения постоянна.

Тогда выражение для полной удельной энергии потока в выбранном сечении примет вид

.

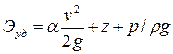Если использовать зависимость 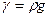,то

 

.

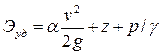Поскольку распределение скоростей в потоке неизвестно, то в гидравлике эти скорости принимаются одинаковыми, а при определении кинетической энергии потока вводится поправочный коэффициент a, учитывающий изменение кинетической энергии вследствие неравномерности распределения скоростей в живом селении потока. Коэффициент a называют коэффициентом кине­тической энергии по имени ученого, открывшего его,— коэф­фициентом Кориолиса. Он может быть определен опытным путем, а при расчетах с достаточной точностью может приниматься: a=1,0—1,13 - для равномерных турбулентных потоков и a=2,0 - для равномерных ламинарных потоков.

Уравнение Бернулли

В потоке жидкости, движущейся в трубке с плавно изменяю­щимся сечением (см. рис. 3.4), выберем два произвольных сече­ния / и //. Обозначим р₁ и p₂ давления в центрах тяжести сечений w₁ и w₂, v₁ и v₂ - средние скорости, а z₁ и z₂— вертикальные координаты оси потока в выбранных сечениях.

Тогда величины полной удельной энергии потока в сечениях / и // соответственно могут быть записаны:

;

.

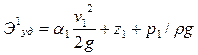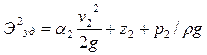При движении реальной жидкости часть энергии затрачивается на преодоление силы трения (сопротивления) на пути от первого сечения до второго. Эта энергия обращается в тепло и рассеивается. Величину указанных потерь энергии обозна­чим h_w. Тогда баланс энергии в сечениях / и // можно записать так:

.

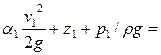
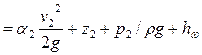Это уравнение называется уравнением Бернулли для реально­го потока жидкости. Оно устанавливает математическую связь между основными элементами движения жидкости, т. е. средней скоростью и гидродинамическим давлением. Оно показывает, что за счет преобразования одного вида энергии в другой наблюдает­ся при возрастании скорости уменьшение давления и, наоборот, при уменьшении скорости — возрастание давления.

Физический (энергетический) смысл уравнения Бернулли со­стоит в том, что при установившемся движении жидкости сум­ма трех удельных энергий (положения, давления и кинетической) остается неизменной.

Легко убедиться, что каждый член уравнения Бернулли име­ет размерность длины и показывает:

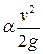- высоту скоростного напора; 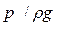пьезометрическую высоту, отсчитываемую в каждом сечении по пьезометру (см. рис. 3.4); z — геометрическую высоту; h_w — потерянный напор, равный части энергии, превращенной в тепло.

Сумма трех высот — скоростного напора, пьезометрической и геометрической — называется гидродинамическим напором:

 

.

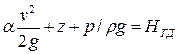⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: