Лабораторная работа № 3 по теме

"Адресация" и "Диаграммы"

1. Табулирование функции. Задание 3.1.

1) Рассчитать таблицу значений функции f(x)= , где x меняется от a до b.

2) Вывести значения функции в n точках этого интервала.

3) Построить график функции.

4) Изменяя значения a, b, n, проследить за изменением функции по её графику.

Выполнение.

1. Задать а= - , b = , n =10. Ввести эти значения в соответствующие ячейки, при вводе использовать функцию ПИ ();.

2. Вычислить шаг изменения функции по формуле: шаг =(b-а)/ n

3. Вычислить значения аргумента х:

Точка 1 - х = а (формула в ячейке B7: =С2);

Точка 2 - х = а + шаг (формула в В8: = B7+C$5);

формула из ячейки В8 копируется на блок ячеек В9:В17.

4. Вычислить значения функции F(x) по формуле:

= 4*EXP(-ABS(B7))-1,

формула из ячейки С7 копируется на блок С8:С17.

5. Диаграмму оформить с помощью Мастера диаграмм.

 

 

Рис.10. Иллюстрация к заданию 3.1.

2. Решение нелинейного уравнения

Задание 3.2. Решить уравнение f(x)= =0 графическим способом.

G Напоминание.

1. Решить уравнение f(x) = 0 означает: найти значения аргумента х, при которых функция f(x) обращается в 0.

2. Решить уравнение графическим способом: найти точки пересечения графика функции с осью ОХ.

Решение.

1) Определить приближённые значения отрезка ОХ, в котором могут быть корни заданного уравнения.

2) Протабулировать функцию f(x)= в этом отрезке оси Х.

3) Построить график функции по полученным табличным значениям.

G Примечание. Для заданной функции первые три пункта решения выполнены в предыдущем задании 3.1.

4) Из графика следует, что функция в заданном отрезке

[- , ] имеет два пересечения оси ОХ, т.е. два корня.

Уточнить последовательно оба корня:

· задать значения а= -1.8, b = -1.2 (в этом отрезке функция переходит через 0). Обратить внимание на изменения в графике и табличные значения f(x). Если полученная точность (f(x)=0 с точностью 0.0063) вас устраивает, то первым корнем уравнения можно считать значение х₁=-1.38.

· Если полученная точность не подходит, то нужно задать новые значения а и b (а= -1.39, b = -1.37).

Получается f(x)=0.003 в точке 3, при х= -1.386.

· Второй корень находится аналогичным образом. Функция симметрична относительно х=0, поэтому х₂=1.386

 

 

Задание 3.3. Решить уравнение f(x)= = 0

Решение. с помощью итераций

§ Установить в ячейке С47 любое начальное значение х из отрезка [-2; 0].

§ Выделить ячейку D47, в которой вы­числяется F(x).

§ Выполнить команду " Сервис/ Подбор параметра ".

В диалоговом окне поле "Устано­вить в ячейке:" уже содержит адрес выделенной ячейки D47.

- в поле "Значение:" ввести 0,

- в поле "Изменяя значение ячейки:" ввести адрес ячейки C47, содержащей величину x, "ОК".

§ Выводится новое окно "Результаты подбора параметра" c найденным решением.

§ Аналогичным образом найти 2-й корень уравнения.

 

3. Построение поверхности сложной функции

Задание 3.4. Построить поверхность по формуле:

для х [0,4] и y [0,3].

Построить сечения и линии уровня[4] поверхности.

§ ввести значения х в столбец А, начиная с А2, автозаполнением с нуля c шагом 0,25 до х=4;

§ ввести значения y в строку 1, начиная с В1, автозаполнением с нуля c шагом 0,25 до y=3;

§ В В2 ввести формулу: EXP(-((A2-2)^2-(A2-2)*(B1-1)+(B1-1)^2));

§ адресам А2 и В1 задать необходимый для копирования формулы по строкам и столбцам тип адресации;

§ скопировать формулу из ячейки В2 на всю таблицу с заданным диапазоном x и y;

§ выделить всю таблицу, включая значения x и y, и построить диаграмму типа " поверхность ";

§ изменить ракурс просмотра диаграммы -«ухватить» угол (+)

диаграмму.

области построения и нажатой левой кнопкой мыши вращать

 

Рис.12. Поверхность задания 3.4

§ Построение линий уровня поверхности - тип диаграммы - "поверхность", проволочная контурная диаграмма (рис. 13а).

§ для построения сечений задать тип диаграммы - "точечная" без маркеров (рис. 13б);

 

 

б)

 

 

а)

 

 

Рис.13. Способы представления поверхности: а) линии уровня;

б) нормальные сечения

Формулы массива

Формулы массива называют также табличными форму­лами. Формулы массива — очень мощное средство Excel, позволяющее в форму­лах обращаться с блоком, как единым целым. Такие формулы позволяют давать компактные решения сложных задач.

Массивы можно использовать для создания формул, которые возвращают некоторое множест-во результатов или оперируют множеством значений, а не отдельными значениями.

Формула массива использует несколько множеств значений, назы-ваемых массивами аргумен-тов, и возвращает одно или несколько значений.

Диапазон массива – это блок ячеек, который имеет общую формулу массива.

 

 

Правила применения формулы массива:

Ø выделить ячейку или диапазон, который будет содержать результаты (диапазон такого же размера и формы, что и диапазон с исходными данными);

Ø нажать Ctrl + Shift + Enter для фиксации ввода формулы массива, Excel заключает формулу в фигурные скобки (указание того, что это формула массива).

Ø редактировать отдельные ячейки массива нельзя.

Ячейки в диапазоне массива рассматриваются как

единое целое, и редактировать их надо все сразу.

Ø для изменения или очистки массива следует выделить весь массив и активизировать строку формул. (Фигурные скобки вокруг формулы исчезнут.) Изменить или очистить формулу и нажать Ctrl + Shift + Enter.

Ø выделить весь массив – щелкнуть на любой ячейке массива нажать Ctrl+/.

Упражнение 6.1. Подсчитать значения столбца "К выдаче" в заданной таблице:

	А	В	С	D
	Фамилия И.О.	Начислено	Удержано	К выдаче
	Петров П.П.
	Иванов И.И.
	Сидоров С.С.
	Козлов К.К.

Решение.

1-й способ:

§ Выделить блок D2:D5 (активной ячейкой в этом блоке является D2); набрать знак =;

§ выделить блок В2:В5, набрать знак минус -;

§ выделить блок С2:С5, нажать сочетание клавиш

Ctrl + Shift + Enter.

§ во всех ячейках блока D2:D5 появится

формула {=B2:B5-C2:C5}

2-й способ:

§ задать имена блокам В2:В5 - "Начислено", С2:С5 - "Удержано" (команда Вставка/ Имя/Присвоить);

§ выделить блок D2:D5 (активной ячейкой в этом блоке является D2); набрать знак =;

§ нажать клавишу F3, в диалоговом окне выбрать имя "Начислено", ОК; набрать знак минус -;

§ нажать клавишу F3, в диалоговом окне выбрать имя "Удержано", ОК;

§ нажать сочетание клавиш Ctrl + Shift + Enter;

во всех ячейках блока D2:D5 появится формула:

{=Начислено - Удержано}.

Упражнение 6.2. Очистить одну из ячеек, занятую таблич-ной формулой

Попытка (пример из упражнения 6.1).

§ выделить ячейку D2;

§ нажать клавишу Del.

§ Получим сообщение:

Удалить блок можно

только целиком!

 

Изменение табличной формулы:

§ выделить блок с фор­мулой (клавиши Ctrl+/),

§ нажать функциональную клавишу F2,

§ внести изменения в формулу,

§ нажать сочетание клавиш Ctrl+Shift+Enter.

Задача 6.1. Ввести формулу {=Начислено - Удержано + 10}, потом отменить это.

Векторы

Векторы — это наборы чисел, расположенные горизонтально (вектор-строка) или вертикально (вектор-столбец).

Ø сложение - два вектора а и b с одинаковым числом компо­нент образуют новый вектор с: с_i = a_i + b_i;

Ø умножение на число - каждая компонента вектора умножает­ся на число, т.е. b = λ а означает b_i = λа_i

здесь i — номер компоненты вектора.

Упражнение 6.1.1. Сложить два вектора:

a) Ввести в первую строку вектор Х - (А1:Е1)

b) Ввести во вторую строку вектор Y - (А2:Е2)

c) Найти сумму векторов –

s выделить блок ячеек для результата в третьей строке (А3:Е3);

s ввести в строке формул =А1:Е1+А2:Е2

s нажать Ctrl+Shift+Enter.

Иллюстрация к примеру - рис. 14.

А В С D E

1

Рис. 14. Иллюстрация к упражнению 6.1.1.

Задача 6.1.1. Умножить вектор на число.

Упражнение 6.1.2.

Умножение вектор-столбца на вектор-строку.

В блоке (вектор-столбце) А2:А5 записаны числа: 1,2,3,4. Требуется получить в блоке B2:D5 три вектор-столбца, каждый из которых представляет собой результат умножения исходного вектор-столбца на вектор-строку: 2, -3, 4 (B1:D1). Рис.15. К упр. 6.1.2.

Решение.

1-й способ: за­писать в ячейку В2 формулу =$А2*В$1 и скопировать ее в ос­тальные ячейки диапазона B2:D5.

2 -й способ (более экономный): выделить блок B2:D5. За­пишем в него формулу массива {=А2:А5*B1:D1}.

Анализ решения. Табличный массив {2;-3;4} - вектор-строка, а блок А2:А5 - вектор-столбец. Значит, матрица B2:D5 размерностью 4Х3 является результатом умножения вектор-столбца А2:А5 (4Х1) на вектор-строку B1:D1 (1Х3).

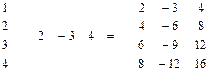
G Примечание. Если ввести формулу {=B1:D1* А2:А5}, то получится тот же результат, хотя с позиций матричной алгебры вектор-строку (1х3) нельзя умножать на вектор-столбец (4х1) из-за несогласованности размеров (число столбцов в первом сомно­жителе должно равняться числу строк во втором сомножителе).

Упражнение 6.1.3. Вычислить скалярное произведение двух векторов.

1) Установить курсор в ячейку, где нужен результат.

2) Щёлкнуть кнопку автосуммы - S.

3) Выделить массив Х (А5:А12).

4) Нажать знак умножить - *.

5) Выделить массив Y (B5:B12).

6) Нажать Ctrl + Shift + Enter.

G Примечание. Тот же результат можно получить с помощью обычной функции: = СУММПРОИЗВ (А5:А12, В5:В12).

Матричные операции

Простейшие операции, которые можно проделывать с мат­рицами: сложение (вычитание), умножение на число, перемно­жение, транспонирование, вычисление обратной матрицы.

Упражнение 6.2.1. Сложение матриц.

Задание. Сло­жить матрицы М и N, где

Решение.

M= и N=

1-й способ:

§ Ввести матрицу М в блок А1:С2, а матрицу N в блок Е1:G2.

§ В блок А4:С5 ввести табличную формулу {= А1:С2 + E1:G2}.

G Примечание. Выделен блок, имеющий те же размеры, что и исходные матрицы.

2-й способ:

Использование имен делает процедуру ввода табличной формулы намного проще:

§ Задать диапазонам А1:С2 и E1:G2 имена М и N.

§ В блок E4:G5 ввести табличную формулу { = М + N }.

Результат, естественно, тот же: M+N =

Упражнение 6.2.2. Вычислить линейную комбинацию матриц 2*М - N (матрицы М.и N из упражнения 6.2.1.).

Решение. В блок А7:С8 ввести табличную формулу {= 2*М - N }.

Результат: 2*M - N =

Задача 6.2.1. Осмысленные результаты (не имеющие ничего общего с матричной алгеброй) получаются при сложе­нии матриц разных размеров. Придумать примеры и попытаться выявить правила, по которым Excel выполняет такое сло­жение.

Для матричных операций в Excel предусмотрены функции, входящие в категорию "Математические":

МОПРЕД — вычисление определителя матрицы;

МОБР — вычисление обратной матрицы;

МУМНОЖ — перемножение матриц;

ТРАНСП — транспонирование.

G Примечание. Первая из этих функций возвращает число, поэтому вводит­ся как обычная формула. Остальные функции возвращают блок ячеек, поэтому они должны вводиться как табличные формулы.

Упражнение 6.2.3. Вычислить определитель и обратную матрицу для матрицы:

А =

 

Решение. Разместить исходную матрицу в блоке А1:СЗ.

1) В ячейке Е2 поместить формулу для вычисления определи­теля = МОПРЕД (А1:СЗ).

2) В блок А5:С7 ввести формулу для вычисления обратной матрицы:

- выделить блок А5:С7 (он имеет три строки и три столбца, как и исходная матрица).

- Ввести формулу {=МОБР (А1:СЗ)}.

G Примечания:

a) При использовании Мастера функций нужно завершать ввод нажатием комбинации клавиш Ctrl+Shift+Enter (вместо щелчка по кнопке "ОК").

b) Для удобства работы рекомендуется задавать имена исходной матрице и обратной матрице.

3) Проверить правильность вычисления обратной матрицы ум­ножением ее на исходную:

- задать имена исходной матрице - А и обратной матрице - АО;

- в блок D5:F7 ввести формулу {=МУМНОЖ (А,АО)}.

- как и следовало ожидать, получилась матрица, близкая к единичной.

 

 

Рис. 16. Иллюстрация к упражнению 6.2.3.

Решение:

Упражнение 6.2.4. Вычислить абсолютные отклонения величин в матрицах.

В блок А9:С11 ввести табличную формулу {= abs (A-AО)}.

Задача 6.2.2. При каком значении элемента а₃₃ определитель матрицы А обратится в нуль.

Задача 6.2.3. Дана матрица S = . Вычислить матрицу 2SS^Т - Е, где Т — операция транспо­нирования,

Е — единичная матрица.

Задача 6.2.4. Вычислить обратную матрицу для

и применить форматирование, чтобы элементы матрицы пред­ставляли собой правильные дроби. Выбрать формат на основе величины определителя матрицы.

G Набор матричных операций в Excel беден.

Если нужно серьезно работать с матрицами, лучше прибегнуть к помощи таких математических пакетов, как MatLAB (Matrix LABoratory), Mathematica, Derive.

 

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: