 |
для расчета постоянной ренты
|
|
|
|
| параметр | функция для его расчёта |
| Современное значение | П3 (ставка, кпер, плата, нз, тип) |
| Будущее значение | Б3 (ставка, кпер, плата, нз, тип) |
| Плата | ППЛАТ (ставка, кпер, нз, бз, тип) = ОСНПЛАТ + ПЛПРОЦ |
| Количество периодов | КПЕР (ставка, плата, нз, бз, тип) |
| Ставка | НОРМА (кпер, плата, нз, бз, тип, нач_прибл) |
G Примечание к таблице:
Математические формулы, являющиеся основой финансовых функций, приведены в справке по функции ПЗ.
Расчет инвестиций
При оценке эффективности инвестиций часто применяют метод расчета чистого текущего объема вклада на основе ряда последовательных поступлений наличных сумм (функция НПЗ). Он позволяет определить нижнюю границу прибыльности и использовать её в качестве критерия при выборе наиболее эффективного проекта. Положительное значение НПЗ является показателем того, что проект приносит чистую прибыль своим инвесторам после покрытия всех связанных с ним расходов. Синтаксис функции:
НПЗ (норма; сумма1; сумма2;...суммаN)
Аргументы функции: норма - процентная ставка за период;
сумма1; сумма2;...суммаN - значения выплат и поступлений.
Если n - это количество денежных взносов Ri в списке значений (R1-выплата в конце 1-го периода, R2-выплата в конце 2-го периода и т.д.), то формула для функции НПЗ (в англ. варианте - NPV) имеет вид:
G Примечание. Считается, что инвестиция, чистую текущую стоимость которой вычисляет функция НПЗ, начинается за один период до даты аргумента сумма1 и заканчивается с последним значением в списке. Если первый денежный взнос приходится на начало первого периода, то первое значение следует добавить (вычесть, если это затраты) к результату функции НПЗ, но не включать в список аргументов (см. упр. 7.4.1.).
|
|
|
Упражнение 7.4.1. Затраты по проекту в начальный момент его реализации составляют 37 000 руб, а ожидаемые доходы за первые пять лет: 8000 руб., 9200 руб., 10 000 руб., 13900руб. и 14 500 руб. На шестой год ожидается убыток в 5000руб. Цена капитала 8% годовых. Рассчитать чистую текущуюстоимость проекта.
Решение: =НПЗ(8%;B1:B5;-5000)-37000 (= 3167,77 руб.)
(доходы занесены в В1:В5).
Упражнение 7.4.2. Определить эффективность инвестиции размером 200млн. руб., если ожидаемые ежемесячные доходы за первые пять месяцев составят соответственно: 20, 40, 50, 80 и 100млн. руб. Издержки привлечения капитала составляют 13,5% годовых.
Решение. =НПЗ(13,5%/12;-200;В1:В5) (=78,30 млн. руб.)
(доходы занесены в В1:В5).
Лабораторная работа № 5
по теме "Финансовые расчёты"
Задание 5.1. Определить, какой из двух вариантов инвестирования средств в течение 4 лет предпочтительнее:
1) в начале каждого года под 26% годовых;
2) в конце каждого года под 38% годовых.
Ежегодно вносится 300 тыс.руб.
Ответы: 1) =2 210,53 тыс.руб; 2) =2 073,74 тыс.руб.
Задание 5.2. Сумма 2000 руб. размещена под 9% годовых на 3 года. Проценты начисляются раз в квартал. Какая сумма будет на счете?
Ответ: =2 612,10 руб.
Задание 5.3. Рассмотреть два варианта покупки дома: заплатить сразу 99000 тыс.руб. или в рассрочку - по 940 тыс.руб. ежемесячно в течение 15 лет. Определить, какой вариант предпочтительнее, если ставка процента - 8% годовых.
Ответ: 2) =98 362,16 тыс.руб. меньше 99 000 тыс.руб.
Задание 5.4. Рассчитать чистый текущий объем инвестиции при покупке обувного магазина. Стоимость предприятия - 40 000 руб., ожидаемые доходы за первые пять лет: 8 000 руб., 9 200 руб., 10 000 руб., 12 000 руб. и 14 500 руб. Годовая учетная ставка равна 8 процентов (она может представлять степень инфляции или учетную ставку конкурирующих инвестиций). Инвестиции начинаются в начале первого периода.
Ответ: 1 922,06 руб.
Предположим, что на шестой год обувной магазин потерпел крах, и предполагается убыток в 9 000 руб. для шестого года. Рассчитать чистый текущий объем инвестиции в обувной магазин после шести лет.
|
|
|
Ответ: -3 749,47 руб.
Задание 5.5.
Рассчитать схему погашения займа в 70 тыс.руб., выданного на 3 года по 17% годовых.
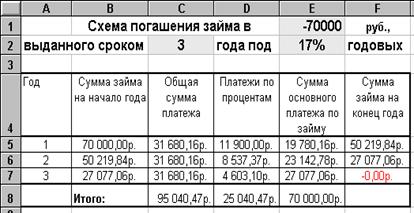Рис.22. Таблица расчётов к заданию 5.5
Пояснения к заданию 5.5.
1) Общая сумма платежа рассчитывается функцией: ППЛАТ (е2;с2;е1).
2) Платежи по процентам вычисляются функцией: ПЛПРОЦ( е2; год; с2; е1), где год - конкретный период, за который выплачиваются проценты (год = 1, 2, 3).
3) Сумму основного платежа по займу можно вычислить как разность между общей суммы платежей и платежам по процентам, например: =с5-d5, далее скопировать формулу на столбец Е.
4) Размер основных выплат по займу можно рассчитать и при помощи функции:
ОСНПЛАТ(е2; год; с2; е1), где год - период, на который вычисляются основные платежи (год = 1, 2, 3).
5) Сумма займа на конец периода =
сумма займа на начало года - сумма основного платежа по займам, или =В5-Е5,
- далее выполнить ссылку этого результата на ячейку В6, затем в ячейку записать формулу =В6-Е6,
- далее снова ссылка на В7, и формула =В7-Е7 в ячейке F7.
6) Итоговая строка рассчитывается автосуммированием.
Список литературы
1. Додж М. Эффективная работа с Microsoft Excel 97: Пер. с англ./ - СПб: Питер,1998. - 1072 с.
2. Долженков В.А. Microsoft Excel 2000 / СПб: БХВ - Санкт-Петербург,1999.- 1088 с.
3. Лавренев С.М. Excel: Сборник примеров и задач. - М.: Финансы и статистика, 2000. - 336 с.
4. Овчаренко Е.К. и др. Финансово-экономические расчёты в Excel. Изд. 3-е/ - М.: Информационно-издательский дом "Филинъ", 1999.-328 с.
5. Гончаров А. Excel 97 в примерах. - СПб: Питер, 1997. - 336 с.
6. Райнер Гебхардт. Excel 97. Справочник / Пер. с нем. - М.: "Издательство БИНОМ", 1998. - 464 с.
7. Задачи по программированию/ С.А.Абрамов, Г.Г.Гнездилова и др.- М.: Наука, 1988. - 224с.
[1] Техника «Drag and Drop» - «Перетащи и оставь» широко используется в программах Microsoft Office.
[2] другое название имени - идентификатор
[3] Диаграмма - графическое представление данных.
[4] Линии равного уровня – совокупность точек, в которых заданная функция принимает равные значения.
[5] Поток - последовательность платежей определённого направ-ления.
|
|
|
