Лабораторная работа № 4 по теме

"Формулы массива "

Задание 4.1. Дана таблица объёма продаж фирмы.

Подсчитать объёмы прибыли.

Формула вычисления суммы произведений данных в столбце С на данные в столбце D:

Кол-во_i * Цена_i = общая стоимость всех изделий

Рис.18. Таблица объёма продаж фирмы (задание 4.1.)

G Примечание. Задание выполнить с помощью

1) формулы массива (см. упр. 6.1.3);

2) обычной функции (примечание к упр.6.1.3);

3) обычной формулы, копирования формулы,

автосуммирования.

Проверить результаты трёх способов.

Задание 4.2. Решить систему уравнений Ах = b

по формуле x = A^-1 b

 

2x₁ - x₂ + 5x₃ = 14 x₁ = 1.7764Е-15 ( 0)

x₁ - 3x₂ + 4x₃ = 9 Ответ: x₂ = 1

3x₁ + x₂ - 7x₃ = - 20 x₃ = 3

 

Задание 4.3. В блоке А1:А10 расположены числа.

Вычис­лить количество чисел блока:

а) являющихся нечетными числами;

{=СУММ(ЕСЛИ(ОСТАТ(А1:А10,2)=0,1,0))}

б) кратных 3 и не кратных 5;

{=СУММ(ЕСЛИ(ОСТАТ(А1:А10,3)=0,

ЕСЛИ(ОСТАТ(А1:А10,5)<>0,1,0),0))}

в) являющихся квадратами целых чисел;

{=СУММ(ЕСЛИ(ОСТАТ(КОРЕНЬ(А1:А10),2)=0,1,0))}

Задание 4.4.

Дана таблица реализации печатной продукции.

N книг	Количество, шт.	Цена за ед. продукции
n/n	январь	февраль	март	январь	февраль	март
				85р.	90р.	100р.
				50р.	65р.	60р.
				70р.	72р.	75р.
				85р.	86р.	90р.
				40р.	45р.	47р.

Подсчитать прибыль за квартал. Формула вычисления

(i - n/n автора и книги, j - номер месяца):

Прибыль за квартал = количество _{i j} * цена _{i j}

G Примечание. Задание выполнить двумя способами:

1) с помощью формулы массива (векторы):

- добавить в таблицу столбец "Стоимость";

- поместить в этот столбец результат скалярного произведения вектора "Количество" и вектора "Цена" для каждой книги

(см. упр. 6.1.3);

- найти общую стоимость всех книг автосуммированием.

2) с помощью формулы массива (матрицы):

- скалярно умножить матрицу "Количество" (все книги за 3 месяца) на матрицу "Цена"(всех книг за 3 месяца) -

{=СУММ(Кол_во*Цена)}

Сравнить результаты обоих способов.

Финансовые расчёты

В Excel имеется большая группа функций (около 50), специ­ально предназначенная для финансовых расчетов. В этой главе рассматриваются только некоторые примеры базовых моделей финансовых расчётов. Более полную информацию о финансовых функциях в Excel можно получить в [4].

Простые проценты

Рассмотрим схему однократного представления некоторой суммы Р в кредит на время t.

За использование кредита надо платить. Возврат кредита составит

S = Р +I.

Плата I носит на­звание "процент" (interest). Чем боль­ше время, на которое выдается кредит, тем больше процент. В простейшем случае полагают I = rt.

 

 

Размерность процентной ставки r (rate of interest) —

ден.ед./год.

 

Например: "Ставка со­ставляет

0.06 руб./год".

 

Принято говорить так: "Ставка состав­ляет 6% годовых в рублях".

 

 

Величина наращенной суммы определя­ется по формуле: S=P(1+rt).

В этой формуле примем, что t = 1 год, тогда

S = Р(1 + r).

 

Отношение S/P =(1+rt) носит название

" ко­эффициент наращения".

Упражнение7.1.1.

Что означает 50% годовых? S = Р(1+0.5) = 1.5 Р, т.е. наращенная сумма в полтора раза боль­ше первоначальной.

А во сколько раз вырастет исходная сумма при 500% годовых? В шесть раз. (Можно сказать иначе: коэффициент наращения равен шести.)

Как проводить вычисления для простых процентов? Началь­ная сумма Р задана, задана ставка процента r (ставка должна быть отнесе­на к году). Время нужно выразить в долях года.

Доля года вычисляется по формуле ,

 

где t — число дней ссуды,

К — число дней в году, или временная база.

 

Измерение времени в финансовых расчётах сопровождается условными соглашениями, которые предлагают два основных подхода:

1) придерживаться точного числа дней в году (365) и точного числа дней в месяцах;

2) считать, что год состоит из 12 месяцев, каждый по 30 дней (360 дней в году).

 

Функция ДОЛЯГОДА (нач_дата, кон_дата, метод)

возвращает частное от деления количества дней между нач_дата и кон_дата на количество дней в году.

В зависимости от выбора метода расчёта задаются параметры

0 (или опущен),1,2.

Упражнение7.1.2. Ссуда в размере 1 млн. руб. выдана 20 янва­ря до 5 октября включительно по 18% годовых. Какую сумму должен заплатить должник в конце срока?

Решение. Обратимся к финансовым функциям.

нач_дата	20-янв
кон_дата	05-окт
ссуда	1 000000
ставка	18%
метод	результат	формулы=
(365/365)	1 12723288	=ссуда*(1 + ДОЛЯГОДА (нач_дата, кон_дата, 1)*ставка)
(360/365)	1 12900000	=ссуда*(1 +ДОЛЯГОДА (нач_дата, кон_дата, 2)*ставка)
(360/360)	1 127500.00	=ссуда*(1 +ДОЛЯГОДА (нач_дата, кон_дата, 0)*ставка)

G Примечание.

При использовании финансовых функций надо учитывать знаки денежных сумм, помня, с чьей точки зрения рассматривается финансовая операция — кредитора или деби­тора.

Положительные платежи означают поступление денег, отрицательные платежи - выплату денег. Поэтому современное и будущее значение связаны соотношением S+P(1+rt)=0, а S и P имеют противоположные знаки.

 

Время в финансовых функциях измеряется в

периодах. Гра­ницы периодов — это моменты

платежей. Период может со­ставлять год,

квартал, месяц, день.

 

 

 

G Примечание. Обычно процентную ставку относят к фиксированному периоду (как правило, году).

Начисление по схеме простых процентов:

S + P(1 + rТ)=0,

 

Начисление по схеме

сложных про­центов:

S + Р(1 + r)^T=0

.

 

Для вычисления наращенной суммы можно использовать функцию БЗ — будущее значение.

 

Эта функция предназначена для вычисления по схеме сложных процентов.

G Примечание. При T = 1 формулы для вычисления S по схеме

простых и сложных процентов совпадают.

Синтаксис БЗ:

Б3 (норма, число периодов, выплата, начальное значение, тип).

Упражнение 7.1.3. Выдан кредит в сумме 1 млн. долл. с

15.01.99 по 15.03.99 под 12% годовых.

Рассчитать сумму погасительного платежа.

Решение. Рассчитать будущее значение исходной суммы можно с помощью функции Б3. Прежде чем воспользоваться этой функцией, следует провести некоторые расчеты.

Число периодов для простых процентов равно 1, но проценты даны годовые. Поэто­му предварительно следует вычислить процентную ставку за указанный в условии задачи период (год).

	А	В	C
	годовая ставка	12%
	дата выдачи кредита	15/01/99
	дата возврата кредита	15/03/99
	сумма кредита	$1 000 000.00
			формулы=
	срок кредита в днях		= В5 - В4
	срок кредита в годах	0.162	= В8 / 365
	ставка для периода	1.94%	= ВЗ * В9
	сумма возврата	-$1 019 397,26	=БЗ (В10,1,,В6)

Рис.19. Таблица расчётов к упражнению 7.1.3.

Результат (платежи!) получился отрицательным.

G Пояснения к упр. 7.1.3. Третий (пропущенный) аргумент функции БЗ - выплаты. Под выплатами подразумеваются промежуточные равные вы­платы в начале (ТИП =1) или в конце (ТИП = 0 или опущен) пе­риода. В этом упражнении выплат нет.

7.2. Сложные проценты

В договорах указы­ваются годовая ставка r и количество начислений процентов m в течение года. Это означает, что базовый период составляет год, деленный на m, а ставка сложных процентов для периода равна r/m. Формула для сложных процентов приобретает вид:

S + P (1 + 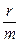)^T = 0 (Т измеряется в периодах).

Если начисление происходит k лет, то формула приобретает вид: S + P (1 + 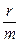)^km = 0.

Упражнение 7.2.1. Ссуда в 20 000 долл. дана на полтора года под ставку 28% годовых с ежеквартальным начислением. Определить сумму конечного платежа.

Решение. Здесь базовый период — квартал. Срок ссуды составляет 6 периодов (4 квартала в году, срок полтора года), за период начисляется 7% = 28%/4. Тогда формула, дающая решение задачи, имеет вид: = Б3 (28%/4, 4 * 1.5,, 20000).

Она возвращает результат: -30 014.61$.

Упражнение 7.2.2. По вкладу размером 2000 тыс. руб начисляется 10% годовых. Рассчитать, какая сумма будет на сберегательном счете через 5 лет, если проценты начисляются ежемесячно.

Решение: БЗ(10%/12;5*12;;-2000) Ответ - 3 290.62 тыс.руб.

Упражнение 7.2.3. На сберегательный счет вносятся платежи по 200 тыс.руб в начале каждого месяца. Рассчитать, какая сумма окажется на счете через 4 года при ставке процента 13,5 годовых.

Решение: =БЗ(13,5%/12;4*12;-200;;1)

Ответ - 12 779,34 т.руб.

 

Сравнить будущее значение счета, если платежи вносятся в конце каждого месяца.

Решение: =БЗ(13,5%/12;4*12;-200) Ответ - 12 637,17 тыс.руб.

Упражнение 7.2.4. Банк принимает вклад на срок 3 месяца с объяв­ленной годовой ставкой 10% или на 6 месяцев под 11%. Как выгоднее вкладывать деньги на полгода: дважды на три месяца или один раз на 6 месяцев?

Решение: Вычислить коэффициенты наращения для обеих предлагаемых схем.

Для 1-ой схемы = Б3(10% * (3/12), 2,,-1000р.) =1 050,63р.,

для 2-ой схемы = Б3(11% * (6/12), 1,,-1000р.) =1 055,00р.

Упражнение 7.2.5. Рассчитать будущее значение вклада 1000 руб. через 0, 1, 2, 3, 4, 5 лет при годовых процентных ставках 10%, 20%,..., 50%.

Дополнительные поступления и выплаты отсутствуют.

Решение.

1) В ячейку В1 поместить величину начального зна­чения вклада;

2) в ячейки B2:G2 разместить числа 0, 1,..., 5 - срок вклада;

3) в ячей­ки АЗ:А7 величины 10%, 20%,..., 50% - процентные ставки;

4) протабулировать функцию двух переменных (процентная ставка и количество лет), зависящую от параметра — начального вклада:

§ ввести в ячейку ВЗ формулу =БЗ($АЗ; В$2;; -$В$1)

§ скопировать формулу в остальные ячейки интервала B3:G7.

5)

изменяя значение в ячейке В1 рассчитать будущую сумму вклада.

Рис. 20. Таблица расчётов упражнения 7.2.5.

Если процентная ставка меняется с течением времени, то для расчёта будущего значения инвестиции (единой суммы) после начисления сложных процентов можно использовать функцию БЗРАСПИС (в англ. варианте - FvSchedule). Синтаксис функции:

БЗРАСПИС (инвестиция, {ставка1; ставка2; …; ставкаN})

G Примечания.

1. Ставки необходимо вводить не в виде процентов, а как числа (0,1; 0,15; 0,05).

2. Вместо массива ставок можно указывать блок ячеек, содержащий процентные ставки.

Упражнение 7.2.6. По облигации номиналом 100 тыс.руб., выпущенной на 6 лет, предусмотрен следующий порядок начисления процентов: в 1-й год -10%, в два последующих года - 20%, в оставшиеся 3 года - 25%.

Рассчитать будущую стоимость облигации по сложной процентной ставке.

Решение: БЗРАСПИС (100, А1:А6) Результат = 309,38

(А1:А6 - 10%, 20%, 20%, 25%, 25%, 25%).

Задача 7.2.1. Построить семейство графиков зависи­мости будущего значения от срока (Упр.7.2.5).

Форматировать шкалу зна­чений как логарифми-ческую

и объяснить вид полученных гра­фиков (рис. 21).

РРис. 21. Семейство графиков к задаче 7.2.1.

Задача 7.2.2. Рассчитать будущую стоимость облигации номиналом $300, выпущенной на 5 лет, если порядок начисления процентов таков: в первые два года -13,5% годовых, в следующие два года - 15%, в последний год - 20%.

Постоянные ренты

До сих пор рассматривался простейший финансовый поток[5]: {-Р, S} или {Р, -S}.

Далее рассматривается схема с многократными взноса­ми или выплатами.

Поток платежей, все члены которого имеют одинаковую ве­личину R (выплаты)и разделены равными промежутками времени, назы­вают

постоянной рентой.

Один из возможных вариантов такого потока

{-Р, -R, -R,,.., -R, S}, т.е.

начальный взнос Р и последующие выплаты R дают в итоге S.

 

Если платежи производятся в конце периодов, то ренту называют обыкновенной, или постнумерандо.

Если же платежи происходят в начале периодов, то ренту называют пренумерандо

Формула,

которую используют функции Excel для расчетов:

Р(1 + r)ⁿ + R(1 + r * type) + S = 0, если r 0,

и Р + Rn + S = 0, если r = 0.

G Примечание. Р — совре­менное (текущее) значение,

S — будущее значение,

R — периодическая выплата,

r — про­центная ставка за период,

n — количество перио­дов,

type — тип ренты,

если type = 0 или опущен, то рента постнумерандо

(выплата в конце периода),

если type = 1, то рента пренумерандо

(выплата в начале перио­да).

Упражнение 7.3.1. На счет в банке вносится сумма 1000 долл. в течение 10 лет равными долями в конце каждого года. Годовая ставка 4%.

Какая будет сумма на счете после 10 лет?

Решение. Платежи осуществляются в конце периодов (рента постнумерандо), поэтому тип = 0 (или его можно опустить). Формула = Б3 (4%; 10; -1000) (аргумент нач_значение также необязательный, и мы его опустили). Ре­зультат: $12006.11.

Если же сумма вносится в начале года (рента пренумерандо), то формула принимает вид:

= Б3 (4%;10; -1000;; 1). Резуль­тат выше: $12486.35.

Разность между этими двумя значениями можно вычислить как: =БЗ(4%;10;0;-1000) -1000.

Задача 7.3.1. Рассматриваются две схемы вложения денег на 3 года: в начале каждого года под 24% годовых или в конце каждого года под 36%. Ежегодно вносится по 4000.

Какая схема выгоднее?

? Как по будущему значению определить современное

значение?

Упражнение 7.3.2. Вексель на 3 000 000 долл. с годовой учетной ставкой 10% с дисконтированием два раза в год выдан на два года.

Найти ис­ходную сумму, выданную под этот вексель.

Решение. Для решения этой задачи воспользуемся функцией

ПЗ — приве­денное (современное) значение.

Синтаксис функции ПЗ:

П3 (норма, кол-во_периодов, выплата, будущее_знач., тип).

Задана ставка дисконта, а аргумент норма подразумевает процентную ставку. Поэтому предварительно нужно пересчитать дисконтную ставку в процентную.

Таблица расчётов к упражнению 7.3.2:

	А	В	C
	Годовая учетная ставка	10%
	Периодичность выплат
	Будущее значение	-$3 000 000.00
	Количество лет
			(формулы:)
	Учетная ставка за период	5.00%	=В1 / В2
	Процент за период	5.26%	=В6 / (1-В6)
	Современное значение	$2 443 518.75	=ПЗ (В7;В2*В4;;ВЗ)

Задача 7.3.2. Рассматриваются два варианта покупки не­движимости: заплатить сразу 70 000 руб. или платить ежемесяч­но по 800 руб. в течение 12 лет при ставке 9% годовых. Какой вариант более выгоден?

?

определить

Как при современном и

продолжительность

заданных будущем значениях,

про­центной ставке

ссуды?

Упражнение 7.3.3. За какой срок в годах сумма, равная

75 000 долл., достигнет 200 000 долл. при начислении процентов по сложной ставке 15% раз в году и поквартально.

Решение. Воспользуемся функцией

КПЕР (норма, выплата, нач. значение, будущее значение, тип)

Решение дается формулами:

1) раз в год = КПЕР (15%; 0; -75; 200) (=7,017856);

2) по кварталам = КПЕР (15% / 4; 0; -75; 200) /4 (=6,660713).

G Примечания.

1. В случае 2) КПЕР возвращает количество кварталов, поэтому, чтобы пересчитать их в годы, нужно поделить возвращаемый результат на 4.

2. Нет ника­кой необходимости набирать все нули в современной и будущей сумме — достаточно сохранить между ними пропорциональ­ность.

Задача 7.3.3. Перевести полученные результаты из дроб-ного числа лет в число лет и дней.

Задача 7.3.4. Почему формула = КПЕР(15%; 0; 75; 200) возвращает ошибочное значение?

Задача 7.3.5. Ссуда 63200 руб., выданная под 32% годовых, погашается ежеквартальными платежами по 8400 руб. Рассчи­тайте срок погашения ссуды.

Как зная современное и будущее значение суммы, а

? также периодические равные вы­платы, вычислить процентную ставку?

Эту задачу решает функ­ция:

НОРМА (кол-во_периодов, выплата, нач_значение, будущее_значение, тип, нач_приближение)

G Примечания.

1) Функция НОРМА возвращает процентную ставку за один период.

2) Начальное_приближение по умолчанию составляет

10%.

Упражнение 7.3.4. Пусть в долг на полтора года дана сумма 2000 долл. с усло­вием возврата 3000 долл. Вычислить годовую процентную став­ку.

Решение: =НОРМА (1,5;; 2000; -3000). Результат: 31%.

Упражнение 7.3.5. Выдан кредит 200 000 долл. на два с половиной года. Про­центы начисляются раз в полгода. Определить величину про­центной ставки за период, если известно, что возврат составит 260 000 долл.

Решение: = НОРМА (2.5*2;; 200000; -260000).

Результат: 5.39%.

G Примечание. В договорах часто указывается именно годовая ставка, даже если период меньше года, то полученный результат следует обработать функцией:

НОМИНАЛ (фактическая ставка, количество периодов в году).

По заданной ставке для периода эта функция возвращает эк­вивалентную годовую ставку.

Упражнение 7.3.6. В условиях предыдущего примера найти годовую ставку.

Решение: =НОМИНАЛ (5.39%;2)

(год составляют два по­лугодия). Результа т: 5.32%.

Наиболее сложной частью анализа постоянной ренты явля­ется определение размера выплат.

Типичная ситуация здесь та­кова. Кредитор выдает в начале срока некоторую сумму. Деби­тор обязуется погасить задолженность равными долями. При этом каждую выплату можно разбить на две составляющих — одна идет на погашение основной задолженности, а другая — на процентные выплаты.

Для вычисления выплат предназначена функция:

ППЛАТ (ставка, кол-во_периодов, нач._значение, будущее_значение, тип ).

G Примечания.

1) Будущее_значение — это баланс наличности, который нужно дос­тичь после последней выплаты. Если будущее значение опу­щено, оно полагается равным 0

(т.е. задолженность погашена).

2) Для нахождения общей суммы, выплачиваемой на протяже­нии интервала выплат, нужно умножить возвращаемое функци­ей ППЛАТ значение на количество периодов.

Функция

ОСНПЛАТ (ставка, период, количество_периодов, нач_значение, будущее значение, тип)

вычисляет часть выплат, которая идет на погаше­ние основной задолженности.

G Примечание. 2-й параметр — период — это порядковый номер пе­риода, для которого производится расчет. Этот номер лежит в интервале от 1 до количество_периодов.

Часть выплат для обслуживания процентов по основному долгу вычисляется с помощью функции:

ПЛПРОЦ (ставка, период, кол-во_периодов, нач_значение, будущее_значение, тип).

Упражнение 7.3.7. Банк выдал долгосрочный кредит в сумме 40 000 долл. на 5 лет под 6% годовых. Погашение кредита должно производиться равными ежегодными выплатами в конце каждого года, вклю­чающими погашение основного долга и процентные платежи. Начисление процентов производится раз в год.

Составить план погашения займа.

Решение. Выплаты составляют постоянную ренту постнумерандо. Результат вычислений представлен в таблице:

	А	В	C	D	Е	F
				Размер кредита	$40000,00
				Срок (лет)
				Ставка	6%
	Годы	Платежи по процентам	Платежи по основному долгу	Годовая выплата (как сумма)	Годовая выплата (как функ­ция)	Остаток долга
		-$2 400.00	-$7 095.86	-$9 495.86	-$9 495.86	$32 904.14
		-$1 974.25	-$7 521.61	-$9 495.86	-$9 495.86	$25 382.54
		-$1 522.95	-$7 972.90	-$9 495.86	-$9 495.86	$17 409.63
		-$1 044.58	-$8 451.28	-$9 495.86	-$9 495.86	$8 958.35
		-$537.50	-$8 958.35	-$9 495.86	-$9 495.86	$0.00
	итоги	-$7 479.28	-$40 000.00	-$47 479.28	-$47 479.28

G Пояснения к таблице расчётов.

В диапазоне Е1:ЕЗ размещены исходные данные.

В форму­лах, осуществляющих решение задачи, используются именован­ные ссылки на эти ячейки, что позволяет сравнивать различные варианты: что, например, будет происходить при изменении процентной ставки.

В строках 6-10 построен план погашения по годам, а в строке 11 помещены итоговые цифры.

Ниже приведены формулы из 6-й строки таблицы:

В6 =ПЛПРОЦ (ставка, А6, срок, размер_кредита)

С6 =ОСНПЛАТ (ставка, А6, срок, размер_кредита)

D6 =C6+B6; Е6 =ППЛАТ (ставка, срок, размер_кредита)

F6 =размер_кредита+С6.

Номер периода берется из первого столбца. При копирова­нии формул номер периода изменяется.

В столбцах D и Е полу­чены, как и следовало ожидать, одинаковые результаты.

В столбце F формулы, начиная с 7-й строки, другие: в ячейке F7 записана формула =F6+C7. Далее она была скопирована в остальные ячейки столбца. Соответственно настроились адреса.

В ячейке В11 помещена формула =СУММ (В6:В10). Аналогич­ные формулы размещены в других ячейках 11-й строки.

G Вывод. При пога­шении долга равными платежами остаток долга с каждой вы­платой уменьшается, следовательно, уменьшаются и процент­ные выплаты.

В результате возрастает от периода к периоду размер платежей, идущих на погашение основного долга.

Задача 7.3.6. Построить совмещенную столбиковую диаграмму, показывающую динамику платежей по годам.

 

 

В Excel имеются функции, позволяющие вычислить платежи сразу за несколько периодов. Функции ОСНПЛАТ, предназна­ченной для расчетов в пределах одного периода, соответствует функция:

ОБЩДОХОД (ставка, кол-во периодов, нач.значение, номер начального периода, номер конечного периода, тип).

Аналогично, функции ПЛПРОЦ соответствует функция ОБЩПЛАТ с теми же аргументами, как и функция ОБЩДОХОД.

Задача 7.3.7. На основе уже созданной таблицы поэкс­периментировать с функциями ОБЩПЛАТ и ОБЩДОХОД. Что получится, если начальный и конечный периоды совпадают, например равны З? Что получится, если начальный период ра­вен 1, а конечный период равен количеству периодов?

 

Таблица 2. Основные парамет­ры

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: