 |
Вывод дифференциального уравнения продольных колебаний стержня с распределенными по длине параметрами.
|
|
|
|
Глава 6. Основные дифференциальные уравнения колебаний механических систем.
Вывод дифференциального уравнения продольных колебаний стержня с распределенными по длине параметрами.
Рассмотрим стержень (Рис. 6.1.1) длиной l, площадью поперечного сечения F (x), модулем упругости E, плотностью ρ(x). Пусть на стержень вдоль оси Ox действует продольная сила с интенсивностью q (x, t). Ось Ox направлена вдоль оси стержня. Функция F (x), ρ (x) и q (x) непрерывны, или кусочно-непрерывны.
Из стержня выделим малый участок Δ x сечениями I-I и II-II, на который действуют следующие силы:
а) продольная внешняя нагрузка, равная q (x, t) Δ x направленная вдоль оси Ox;
| Рис 6.1.1 |
,
где u – упругое перемещение;
в) равнодействующая натяжения со стороны правого участка II-II, равная S (x +Δ x, t)= F (x)Δ(x + Δ x, t) и направлено по оси Ox. Здесь Δ (x + Δ x, t) напряжение в сечении II-II;
г) сила сопротивление среды. Если её интенсивность по длине стержня обозначить через Ф (x, t,υ), то на участок Δ x придётся сила Ф (x, t,υ) Δ x.
Так как сила сопротивления направлена противоположно скорости, то её знак определяется характером её зависимости. Например, для кулонова трения сила сопротивления запишется в виде
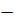Ф sign 
,
где 
,
Для случая, когда сила сопротивления пропорциональна первой степени скорости, знак минус перед Ф сохраняется и опускается sign .
Сила инерции малого элемента стержня определяется выражением
Тогда по принципу Даламбера
|
|
|
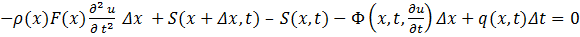(6.1.1)
Разлагая S (x + 
x, t) в ряд Тейлора поставляя в (6.1.1), после деления на Δ x и перехода к приделу при Δ x 
0 получим
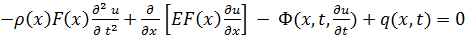(6.1.2)
Аналогичный результат может быть получен, если в результате разложения S (x + Δ x; t) пренебречь членами, содержащими Δ x степени выше второй. В дальнейшем, учитывая это обстоятельство при выводе других дифференциальных уравнений, в разложениях будем оставлять два члена разложения, подразумевая, что имеет место такой придельный переход.
Таким образом, получено дифференциальное уравнение вынужденных колебаний однородного стержня в среде с сопротивлением. Из этого уравнения можно получить в качестве частных случаев уравнения продольных колебаний стержня при различных предположениях относительно распределения массы, жёсткости, сопротивления среды и внешней нагрузки.
Например, если принять ρ(x)= const, F (x)= const, а также принять пропорциональность силы сопротивления скорости, то получится дифференциальное уравнение вынужденных продольных колебаний однородного стержня
g(x,t) (6.1.3)
где 
; g (x, t)= 
; h – коэффициент сопротивления.
Приняв g (x; t)=0, получим дифференциальное уравнение свободных колебаний однородного стержня
(6.1.4)
При h =0 из (6.1.4) получится уравнение свободных колебаний стержня в идеальной среде.
= a 2 
(6.1.5)
Для решения дифференциальных уравнений в частных производных необходимо задание начальных и граничных условий.
В качестве начальных условий обычно задается значения функции и ее первой производной по аргументу t в момент времени 
. При задании только начальных условий совместно с дифференциальным уравнением имеет место задача Коши. Начальные условия для уравнения типа (1.5) могут быть записаны в виде
|
|
|
(6.1.6)
где 
заданные функции.
В качестве граничных условий задаются значения функции и ее производных в некоторых фиксированных точках. Так, например если известен закон движения обоих концов стержня, то эти условия задаются в виде
(6.1.7)
Если на одном из концов известна внешняя действующая сила, то согласно закону Гука
или 
, где 
.
Следовательно 
Тогда граничное условие имеет вид
(6.1.8)
В случае, если на концах стержня имеет место упругое закрепление, то граничное условие составляются исходя из равенства силы натяжения пружины силе реакции конца стержня, т.е.
(6.1.9)
где с – жесткость пружины.
Если точки закрепления являются подвижными и их перемещения задаются функциями типа S (t), то граничные условия (6.1.9) примет вид
(6.1.10)
Различные комбинации указанных выше граничных условий приводят к специальным граничным условиям. Так, например, если на одном конце стержня задается закон перемещения, а на другом – упругая заделка, то получается смешанная задача:
(6.1.11)
Для неограниченного стержня вместо полной задачи можно рассматривать задачу только с начальными условиями – задачу Коши:
При изучении динамики стержня вблизи одной границы влиянием другой границы можно пренебречь, если она на протяжении интересующего нас промежутка времени не оказывает существенного влияния на рассматриваемую часть стержня. При этом стержень можно рассматривать как полу-бесконечный. Задача формулируется а виде:
(6.1.12)
К таким задачам можно отнести изучение динамики верхней части колонны труб достаточно большой длины в процессе торможения или же при ее посадке на клиновой захват; определение давления жидкости или газа в начале трубопровода при пуске насоса или компрессора; определение давления жидкости внутри обсадной колонны при закрытии превентера для предотвращения выброса из скважины и т.д.
Если в качестве граничного условия задана периодическая функция времени, влиянием начальных условий после определенного времени можно пренебречь. Такие задачи называются «задачами без начальных условий» и формулируются следующим образом:
|
|
|
найти решение уравнения
| (6.1.13) |
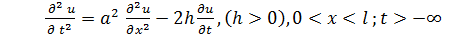
при заданных граничных условиях
|
|
|
