 |
Вывод дифференциальных уравнений поперечных колебаний балки.
|
|
|
|
| Рис 6.2.1 |
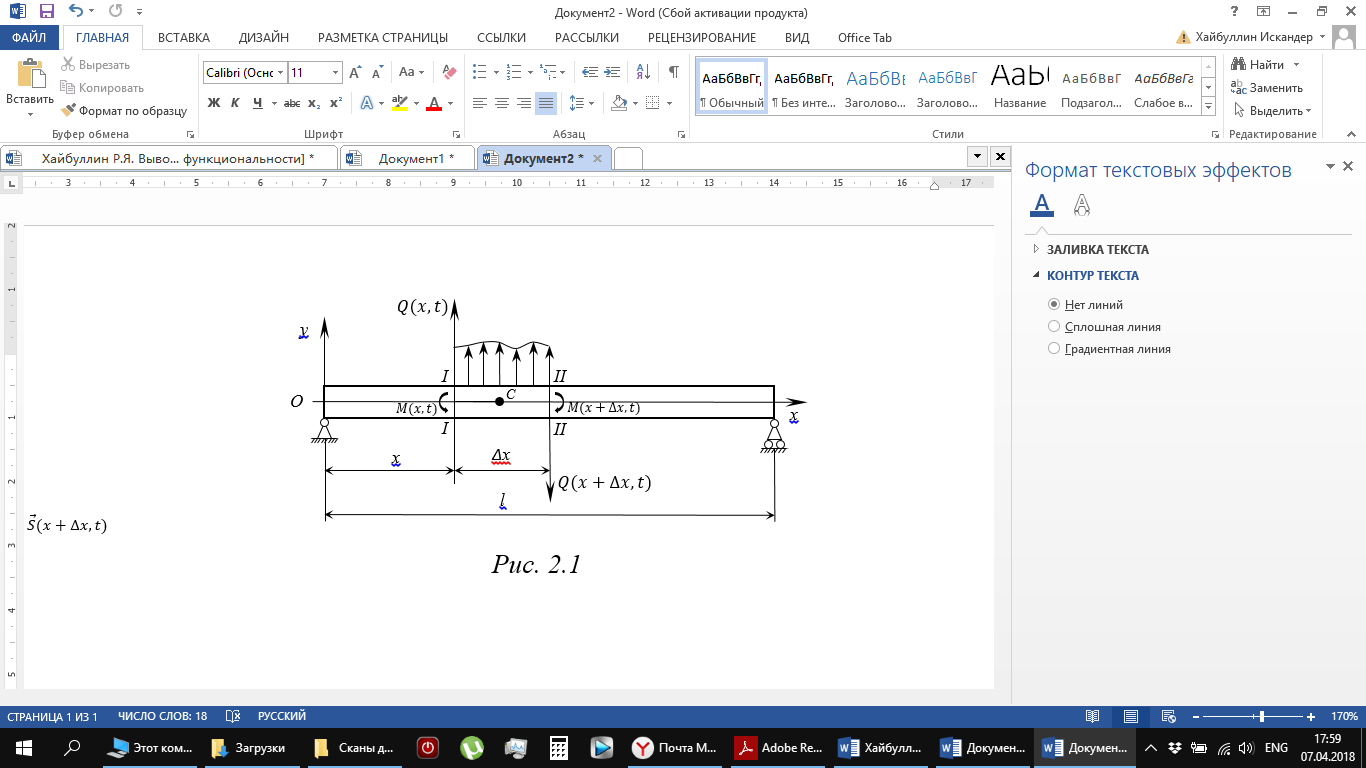Рассмотрим балку, установленную на двух опорах (Рис.6.2.1). Пусть масса единицы длины балки равна μ; модуль упругости материала – E; момент инерции поперечного сечения балки относительно нейтральной оси, перпендикулярной к плоскости чертежа – J; момент инерции единицы длины балки относительно центральной оси, перпендикулярной к плоскости его колебаний – I0.
Принимается, что в недеформированном состоянии ось балки прямолинейна и совпадает с осью Ox. Отклонение точек оси балки при поперечных колебаниях перпендикулярно оси Ox обозначим через u (x; t). Выделим элемент балки сечения I-I и II-II. В сечении I-I действует поперечная сила Q (x; t) и изгибающий момент M (x; t), а в сечении II-II – Q (x + Δ x; t) и M (x + Δ x; t). Интенсивность внешней нагрузки, действующей на балку равна f (x; t).
Под действием указанных сил и моментов выделенный элемент будет совершать плоскопараллельное движение. Так как смещением по оси Ox пренебрегают, то остается составить одно уравнение по принципу Даламбера для сил в проекциях на ось Oy и одно уравнение моментов относительно центра инерции элемента.
Масса элемента равна μ Δ x, а ее осевой момент инерции относительно центральной оси, перпендикулярной к плоскости xOu, равен I 0 Δ x. Угол поворота элемента вокруг той же оси обозначим через φ. Для малых углов поворота φ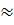 
tgφ = 
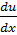. Сила инерции малого элемента при перемещении по оси Oy равна μΔ x 
, а момент силы инерции относительно центральной оси элемента, перпендикулярной к плоскости xOu равен I 0 Δ x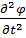 
.
Составим уравнения равновесия проекций и моментов указанных сил:
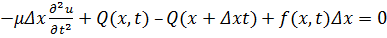(6.2.1)
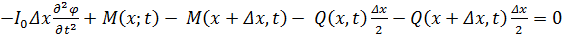(6.2.2)
Разложив в ряд Тейлора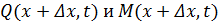 
и оставив первые два члена разложения, получим
|
|
|
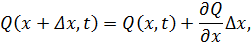
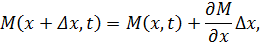
Подставляем эти выражения в (6.2.1) и (6.2.2)
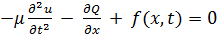(6.2.3)
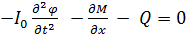(6.2.4)
Из уравнения (6.2.4) следует: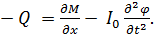 
. Подставляя это выражение в (6.2.3), получим
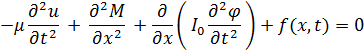
Учитывая, что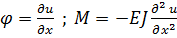 
:
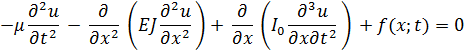
При I 0 = const, EJ = const получим уравнение поперечных колебаний однородной балки в виде
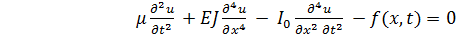(6.2.5)
При длине балки, значительно превосходящей поперечные размеры, инерцией вращения можно пренебречь. Тогда уравнение примет вид:
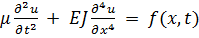(6.2.6)
если принять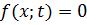 
, получится дифференциальное уравнение свободных поперечных колебаний однородной балки
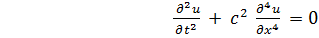(6.2.7)
где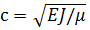 
- скорость распространения поперечных волн.
Для поперечных колебаний балки в качестве начальных условий задаются начальное смещение и начальная скорость балки
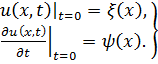(6.2.8)
Граничные условия определяются в зависимости от способа закрепления концов балки. Причем количество условий определяется высшим порядком производной по x в уравнении (6.2.5). Следовательно, должно быть задано четыре условия. Если концы балки закреплены шарнирно, то это значит что на обоих концах его смещение и изгибающие моменты равны нулю, т.е.
Известно, что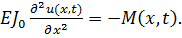 
Следовательно, для балки, шарнирно закрепленного на обоих концах, имеют место следующие граничные условия:
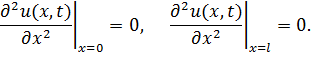
Для консольной балки граничные условия при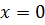 
будут определяться исходя из того, что на защемлённом конце отсутствует прогиб и равен нулю угол поворота сечения балки, т.е.
а для свободного конца, т.е. при 
, если отсутствуют изгибающий момент и поперечная нагрузка можно написать
так как 
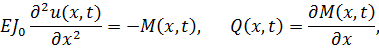
то для консольной балки окончательно получим следующие граничные условия:
| (6.2. 9) |
|
|
|
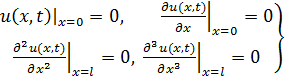
Если на свободном конце будут действовать момент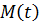 
и поперечная сила 
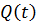, то граничные условия при будут иметь вид
| (6.2. 10) |
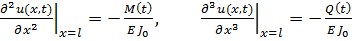
Для балки с жестко закрепленными концами модно принять, что прогибы и углы поворота сечений в местах защемления равны нулю. Тогда
| (6.2. 11) |
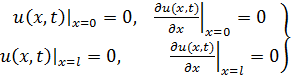
Аналогично можно составить граничные условия и для других видов закрепления концов балки.
|
|
|
