 |
Вывод дифференциального уравнения нестационарного движения сжимаемой идеальной жидкости в длинном трубопроводе.
|
|
|
|
| Рис.6.5.1 |
Выделим в потоке жидкости в трубе два поперечных сечения с расстоянием Δ x между ними (Рис 6.5.1). Введем обозначения: ρ – плотность жидкости или газа; p – среднеедавление в сечении; f – площадьпоперечного сечения; v – осредненная по площади продольная скорость; x – координата; t – время. Составим баланс массы втекающей и вытекающей из элемента потока Δ x.
Массовый расход через сечение I - I будет 
, а через сечение II - II 
.
Если 
, то в объеме 
произойдет уменьшение плотности. Если в момент времени t плотность выделенного объема была равна 
, то уменьшение массы жидкости в объеме равно
(6.5.1)
Разность масс, входящих и выходящих через соответствующие сечения I - I и II - II за промежуток времени Δ t, равна
(6.5.2)
Приравняв (6.5.1) и (6.5.2), получим
Подстановка сюда выражения M дает
. (6.5.3)
Уравнение (6.5.3) представляет собой уравнение неразрывности потока для сжимаемой жидкости в длинном трубопроводе с постоянным поперечным сечением.
Теперь составим уравнение движения выделенного элемента с массой 
Если силу давления в сечении I - I обозначим через P (x, t), а в сечении II - II P (x + Δ x,t), то проекция равнодействующей этих сил на ось x будет
(6.5.4)
Тогда уравнение движения примет вид
или
. (6.5.5)
Уравнение (6.5.5) есть дифференциальное уравнение движения сжимаемой жидкости в длинном прямом трубопроводе с постоянным поперечным сечением.
Уравнения (6.5.3) и (6.5.5) образую систему
(6.5.6)
в которую входят три неизвестные величины: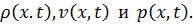 
Следовательно должно быть задано физическое уравнение, устанавливающее зависимость между плотностью и давлением. Для случая капельной сжимаемой жидкости, согласно закону Гука, изменение плотности жидкости принимается пропорциональным изменению давления
|
|
|
(6. 5.7)
где 
– модуль объемного сжатия жидкости; 
– плотности при давлении 
Из (5.7) получаем 
. (6.5.8)
Подставляем (5.8) в (5.6) получим:
(6.5.9)
Для малых дозвуковых скоростей движение идеальной жидкости с равномерным распределением скоростей в сечении в уравнениях движения можно пренебречь членами 
. Тогда система (5.9) примет вид
(6.5.10)
Для случая малых изменений плотности можно принять 
. Тогда (5.10) примет вид
(6.5.11)
Дифференцируя первое уравнение системы по x и второе по t
Тогда получим
Обозначив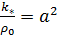 
получим
(6.5.12)
Уравнение (6.5.12) есть дифференциальное уравнение описывающее изменение давления капельной идеальной жидкости в длинном трубопроводе постоянного сечения.
| (6.5.13) |
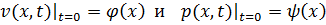
| (6.5.14) |
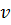или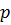 
. Так, например, при помощи зависимости
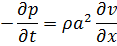
условие (6.5.12) можно представить в виде
| (6.5.15) |
Обычно переходный режим в трубопроводе создается при пуске насоса, турбины компрессора, открытии или закрытии задвижек. При этом указанные агрегаты могут быть присоединены к трубопроводу непосредственно или же через устройства, предназначенные для регулирования расхода или уменьшения колебаний давления (например, воздушный колпак, уравнительная шахта, буферный резервуар компрессора и т.п.).
|
|
|
В случае если к одному концу трубопровода непосредственно присоединен насос с расходом 
а на другом конце задано давление, граничные условия можно представить в виде
| (6.5.16) |
где F – поперечное сечение трубопровода.
Пользуясь уравнением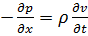 
, условие при 
в (6.5.16) можно представить так:
| (6.5.17) |
Тогда задача о распределении давления в длинном трубопроводе, к одному концу которого присоединен насос с расходом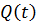 
, а на другом конце поддерживается давление 
, формулируется следующим образом:
| (6.5.18) |
Если насос отделен от трубопровода воздушным колпаком, для составления граничных условий при следует составить уравнение баланса для жидкости и уравнение состояния для воздуха, находящегося в воздушном колпаке.
Обозначим расход жидкости, вытекающей из колпака через 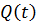, увеличение объема жидкости (или уменьшение объема газа) в колпаке через 
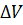, площадь трубопропвода через F, средний объем и абсолютное давление воздуха в колпаке через 
и 
. Прирост объема жидкости в колпаке в единицу времени будет
| (6.5.19) |
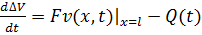
Если принять, что уравнение состояния для воздуха описывается законом Бойля-Мариотта, получится
| (6.5.20) |
т.е. можно принять 
Подставляем значение 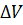из (6.5.20) в (6.5.19):
Учитывая (6.5.14) получим
Отсюда
| (6.5. 21) |
где 
; 
.
Выражение (6.5.21) является граничным условием для длинного трубопровода, к одному из концов которого через воздушный колпак присоединен насос. В этом случае задачу о переходном процессе в трубопроводе можно сформулировать в виде:
| (6.5. 22) |
|
|
|
